Observation 6.8.1.
The name of the order is based on where the root is visited; in preorder, we visit it first. For inorder, we visit it in the middle, and for postorder, we visit it last.
Section 6.8 Tree Traversals
Now that we have examined the basic functionality of our tree data structure, it is time to look at some additional usage patterns for trees. These usage patterns can be divided into three commonly used patterns to visit all the nodes in a tree. The difference between these patterns is the order in which each node is visited. We call this visitation of the nodes a tree traversal. The three traversals we will look at are called preorder, inorder, and postorder. Let’s start out by defining these three traversals more carefully, then look at some examples where these patterns are useful.
- Preorder
- In a preorder traversal, we visit the root node first, then recursively do a preorder traversal of the left subtree, followed by a recursive preorder traversal of the right subtree.
- Inorder
- In an inorder traversal, we recursively do an inorder traversal on the left subtree, visit the root node, and finally do a recursive inorder traversal of the right subtree.
- Postorder
- In a postorder traversal, we recursively do a postorder traversal of the left subtree and the right subtree followed by a visit to the root node.
Let’s look at some examples that illustrate each of these three kinds of traversals. First let’s look at the preorder traversal using a book as an example tree. The book is the root of the tree, and each chapter is a child of the root. Each section within a chapter is a child of the chapter, each subsection is a child of its section, and so on. Figure 6.8.2 shows a limited version of a book with only two chapters. Note that the traversal algorithm works for trees with any number of children, but we will stick with binary trees for now.
Suppose that you wanted to read this book from front to back. The preorder traversal gives you exactly that ordering. Starting at the root of the tree (the Book node) we will follow the preorder traversal instructions. We recursively call
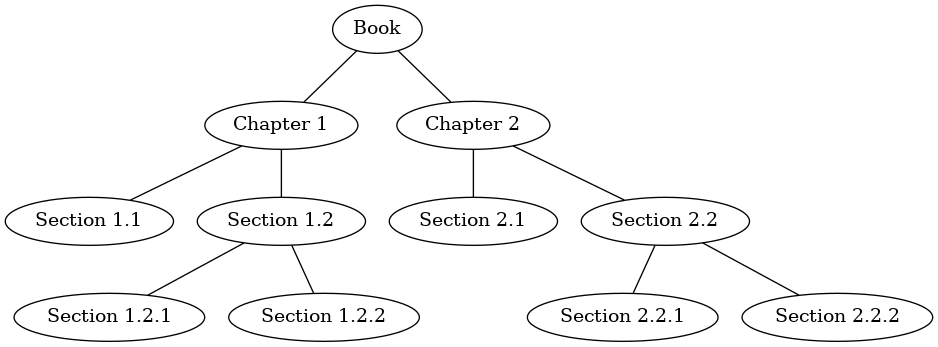
preorder on the left child, in this case Chapter1. We again recursively call preorder on the left child to get to Section 1.1. Since Section 1.1 has no children, we do not make any additional recursive calls. When we are finished with Section 1.1, we move up the tree to Chapter 1. At this point we still need to visit the right subtree of Chapter 1, which is Section 1.2. As before we visit the left subtree, which brings us to Section 1.2.1, then we visit the node for Section 1.2.2. With Section 1.2 finished, we return to Chapter 1. Then we return to the Book node and follow the same procedure for Chapter 2.The code for writing tree traversals is surprisingly elegant, largely because the traversals are written recursively. You may wonder, what is the best way to write an algorithm like preorder traversal? Should it be a method that uses a tree as a data structure, external to the
BinaryTree class, or should it be a method of the tree data structure itself? Listing 6.8.3 shows a version of the preorder traversal written as a static method that takes a binary tree as a parameter. The static method is particularly elegant because our base case is simply to check if the tree exists. If the tree parameter is null, then the function returns without taking any action.public static void preorder(BinaryTree<String> tree) {
if (tree != null) {
System.out.println(tree.getRootValue());
preorder(tree.getLeftChild());
preorder(tree.getRightChild());
}
}
We can also implement
preorder as a method of the BinaryTree class. The code for implementing preorder as an internal method is shown in Listing 6.8.4. Notice what happens when we move the code from external to internal. In general, we just replace tree with this. Also, because this method is part of BinaryTree, it can directly access the fields. However, we also need to modify the base case. The internal method must check for the existence of the left and the right children before making the recursive call to preorder.public void preorder() {
System.out.println(this.key);
if (this.leftChild != null) {
this.leftChild.preorder();
}
if (this.rightChild != null) {
this.rightChild.preorder();
}
}
Which of these two ways to implement
preorder is best? The answer is that implementing preorder as an external method is probably better in this case. The reason is that you very rarely want to just traverse the tree and print its values. In most cases, you will want to accomplish something else while using one of the basic traversal patterns. In fact, we will see in the next example that the postorder traversal pattern follows very closely with the code we wrote earlier to evaluate a parse tree. Therefore, we will write the rest of the traversals as external methods.The algorithm for the
postorder traversal, shown in Listing 6.8.5, is nearly identical to preorder except that we move the call to print to the end of the function.public static void postorder(BinaryTree<String> tree) {
if (tree != null) {
postorder(tree.getLeftChild());
postorder(tree.getRightChild());
System.out.println(tree.getKeyValue());
}
}
We have already seen a common use for the postorder traversal, namely evaluating a parse tree. Look back at Section 6.7 again. The algorithm evaluates the left subtree, evaluates the right subtree, and combines them in the root through the function call to an operator. Assuming our binary tree is going to store only expression tree data, we rewrite the evaluation function, but model it even more closely on the postorder code in Listing 6.8.5.
public static Double postorderEvaluate(BinaryTree>String> tree) {
Double leftValue = null;
Double rightValue = null;
Double result;
if (tree != null) {
leftValue = postorderEvaluate(tree.getLeftChild());
rightValue = postorderEvaluate(tree.getRightChild());
if (leftValue != null && rightValue != null) {
String operator = tree.getRootValue();
if (operator.equals("+")) {
result = leftValue + rightValue;
} else if (operator.equals("-")) {
result = leftValue - rightValue;
} else if (operator.equals("*")) {
result = leftValue * rightValue;
} else {
result = leftValue / rightValue;
}
return Double.doubleValu(result);
}
return Double.parseDouble(tree.getRootValue());
} else {
return null;
}
}
Notice that the form in Listing 6.8.5 is the same as the form in Listing 6.8.6, except that instead of printing the key at the end of the function, we return it. This allows us to save the values returned from the recursive calls in lines 11 and 12. We then use these saved values along with the operator on line 14.
The final traversal we will look at in this section is the inorder traversal. In the inorder traversal we visit the left subtree, followed by the root, and finally the right subtree. Listing 6.8.7 shows our code for the inorder traversal. Notice that in all three of the traversal functions we are simply changing the position of the
System.out.println call with respect to the two recursive function calls.public static void inorder(BinaryTree<String> tree) {
if (tree != null) {
inorder(tree.leftChild);
System.out.println(tree.key);
inorder(tree.rightChild);
}
}
If we perform an inorder traversal of a parse tree, we get our original expression back without any parentheses. Let’s modify the basic inorder algorithm to allow us to recover the fully parenthesized version of the expression as a string. The only modifications we will make to the basic template are as follows: put a left parenthesis before the recursive call to the left subtree, and put a right parenthesis after the recursive call to the right subtree. The modified code is shown in Listing 6.8.8.
public static String expressionToString(BinaryTree<String> tree) {
String result = "";
if (tree != null) {
result = result + "(" + expressionToString(tree.leftChild);
result = result + tree.key;
result = result + expressionToString(tree.rightChild) + ")";
}
return result;
}
Notice that the
expressionToString method as we have implemented it puts parentheses around each number. While not incorrect, the parentheses are clearly not needed. In the exercises at the end of this chapter you are asked to modify the expressionToString function to remove this set of parentheses.You have attempted of activities on this page.
