Section 3.23 Implementing an Ordered List
In order to implement the ordered list, we must remember that the relative positions of the items are based on some underlying characteristic. The ordered list of integers given above (17, 26, 31, 54, 77, and 93) can be represented by a linked structure as shown in Figure 3.23.1. Again, the node and link structure is ideal for representing the relative positioning of the items.

As we consider the operations for the ordered list, we should note that the
isEmpty and size methods can be implemented the same as with unordered lists since they deal only with the number of nodes in the list without regard to the actual item values. Likewise, the remove method will work just fine since we still need to find the item and then link around the node to remove it.The current
add method needs to change. Instead of inserting new items at the head of the list, we must find the correct position for the insertion so that elements don’t get out of order. We can also improve the search method. Instead of scanning all the way to the end of the list to find if an element is in the list or not, we can take advantage of the fact that the list is in order and stop if we find an item in the list that is greater than the one we’re looking for.For both these changes, we will need to compare the items in the list to the item we’re adding or searching for in order to get the correct position in the list. We will do this by invoking the
compareTo method on one of the objects, which we’ll call this. compareTo compares this to another object. It returns a negative number if this is less than the other object, zero if they are equal, and a positive number if this is greater than the other object. The following output from jshell shows this method with String objects.jshell> "cat".compareTo("dog");
$1 ==> -1
jshell> "zebra".compareTo("elephant");
$2 ==> 21
jshell> "giraffe".compareTo("giraffe");
$3 ==> 0
Rather than copy and paste all of the code that is the same, we can use Java inheritance to allow one class to inherit all the properties and methods of another class by using the
extends keyword. Here is the start of the class and the constructor:class OrderedList<T extends Comparable<T>> extends UnorderedList<T> {
public OrderedList() {
super();
}
}
The first line looks very different from what you normally see in Java inheritance, as detailed in Section A.3. Let’s unpack it. Since we’re using generics, we need to put a
<T> on the child class OrderedList and the parent class UnorderedList. We also need to tell Java that it can only allow types that have a compareTo method. That’s what extends Comparable<T> does for us.In the constructor, we call
super() on line 3. This invokes the zero-argument constructor, which sets the head to null. If we had additional properties in the subclass, we would follow the call to super() with their initialization. The call to super() must be the first non-comment statement in the constructor!Because all the methods from
UnOrderedList are inherited, we can immediately use the methods from UnorderedList without having to repeat them in OrderedList:OrderedList MethodsWith this output:
Is list empty? true After adding 505, 217, and 1066: [1066, 217, 505] Is 505 in the list? true Is 300 in the list? false
Recall that for unordered lists, the
add method could simply place a new node at the head of the list. It was the easiest point of access. Unfortunately, this will no longer work with ordered lists; we see from the output that the numbers are in the wrong order. It is now necessary that we discover the specific place where a new item belongs in the existing ordered list.Assume we have the ordered list consisting of 17, 26, 54, 77, and 93 and we want to add the value 31. The
add method must decide that the new item belongs between 26 and 54. Figure 3.23.3 shows the setup that we need. As we explained earlier, we need to traverse the linked list looking for the place where the new node will be added. We know we have found that place when either we run out of nodes (current becomes null) or the value of the current node becomes greater than the item we wish to add. In our example, seeing the value 54 causes us to stop.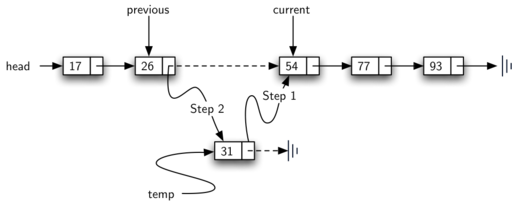
We will write a new version of
add in the OrderedList class. This method will override the method in the parent class (UnorderedList). When we call the add method on an ordered list, Java will call our new method.As we saw with unordered lists, it is necessary to have an additional reference, again called
previous, since current will not provide access to the node that must be modified. Listing 3.23.4 shows the complete add method. Lines 2–3 set up the two references, and lines 6–7 again allow previous to follow one node behind current every time through the iteration. The condition (line 5) allows the iteration to continue as long as there are more nodes and the value in the current node is less the item. In either case, when the iteration fails, we have found the location for the new node.The remainder of the method completes the two-step process shown in Figure 3.23.3. Once a new node has been created for the item in line 9, the only remaining question is whether the new node will be added at the beginning of the linked list or some place in the middle. Again,
previous == null (line 11) can be used to provide the answer.public void add(T item) {
Node<T> current = this.getHead();
Node<T> previous = null;
while (current != null && (current.getData()).compareTo(item) < 0) {
previous = current;
current = current.getNext();
}
Node<T> itemNode = new Node<T>(item);
if (previous == null)
{
itemNode.setNext(this.getHead());
this.setHead(itemNode);
} else {
itemNode.setNext(current);
previous.setNext(itemNode);
}
}
add Method for an OrderedListOnce we recompile the
OrderedList and run our test program (Listing 3.23.2) again, we get the correct results:Is list empty? true After adding 505, 217, and 1066: [217, 505, 1066] Is 505 in the list? true Is 300 in the list? false
The search of an unordered linked list required that we traverse the nodes one at a time until we either find the item we are looking for or run out of nodes (
null). As we said before, the same approach would work with the ordered list and no changes are necessary if the item is in the list. However, in the case where the item is not in the list, we can take advantage of the ordering to stop the search as soon as possible.For example, Figure 3.23.5 shows the ordered linked list as a search is looking for the value 45. As we traverse, starting at the head of the list, we first compare against 17. Since 17 is not the item we are looking for, we move to the next node, in this case 26. Again, this is not what we want, so we move on to 31 and then on to 54. Now, at this point, something is different. Since 54 is not the item we are looking for, our former strategy would be to move forward. However, due to the fact that this is an ordered list, that will not be necessary. Once the value in the node becomes greater than the item we are searching for, the search can stop and return
false. There is no way the item could exist further out in the linked list.
Listing 3.23.6 shows the complete
search method. We can incorporate the new condition discussed above by adding another check (line 6). We continue to look forward in the list (line 3). If any node is ever discovered that contains data greater than the item we are looking for, we will immediately return false. The remaining lines are identical to the unordered list search.public boolean search(T item) {
Node<T> current = this.getHead();
while (current != null) {
if (current.getData().equals(item)) {
return true;
}
if (current.getData().compareTo(item) > 0) {
return false;
}
current = current.getNext();
}
return false;
}
search Method for an OrderedListThe
OrderedList class with methods discussed thus far is in Listing 3.23.7 along with documentation of its methods. We leave the remaining methods as exercises. You should carefully consider whether the unordered implementations will work given that the list is now ordered. If they will, you don’t need to duplicate them; inheritance will do the job for you.class OrderedList<T extends Comparable<T>> extends UnorderedList<T> {
// No extra properties in this class; they are inherited from
// UnorderedList.
/*
* Call superclass constructor to set the head property
* to null.
*/
public OrderedList() {
super();
}
/*
* Add given item at its correct position in the list.
* Presume that the item is not already in the list.
*/
public void add(T item) {
Node<T> current = this.getHead();
Node<T> previous = null;
while (current != null && (current.getData()).compareTo(item) < 0) {
previous = current;
current = current.getNext();
}
Node<T> itemNode = new Node<T>(item);
if (previous == null)
{
itemNode.setNext(this.getHead());
this.setHead(itemNode);
} else {
itemNode.setNext(current);
previous.setNext(itemNode);
}
}
/*
* Check to see if the given item is in the list.
* Return true if it is, false if not.
*/
public boolean search(T item) {
Node<T> current = this.getHead();
while (current != null) {
if (current.getData().equals(item)) {
return true;
}
if (current.getData().compareTo(item) > 0) {
return false;
}
current = current.getNext();
}
return false;
}
}
OrderedList ClassSubsection 3.23.1 Analysis of Linked Lists
To analyze the complexity of the linked list operations, we need to consider whether they require traversal. Consider a linked list that has \(n\) nodes. The
isEmpty method is \(O(1)\) since it requires one step to check the head reference for null. size, on the other hand, will always require \(n\) steps since there is no way to know how many nodes are in the linked list without traversing from head to end. Therefore, size is \(O(n)\text{.}\) Adding an item to an unordered list will always be \(O(1)\) since we simply place the new node at the head of the linked list. However, search and remove, as well as add for an ordered list, all require the traversal process. Although on average they may need to traverse only half of the nodes, these methods are all \(O(n)\) since in the worst case each will process every node in the list.You may also have noticed that the performance of this implementation differs from the actual performance given earlier for ArrayLists. This suggests that linked lists are not the way ArrayLists are implemented. The actual implementation of an ArrayList is based on the notion of an array. We discuss this in more detail in the last chapter.
You have attempted of activities on this page.

