DS Implementing Breadth-First Search

Section 7.9 Implementing Breadth-First Search

With the graph constructed we can now turn our attention to the algorithm we will use to find the shortest solution to the word ladder problem. The graph algorithm we are going to use is called the breadth-first search (BFS), and it is one of the easiest algorithms for searching a graph. It also serves as a prototype for several other important graph algorithms that we will study later.

Given a starting vertex \(s\) of a graph \(G\text{,}\) a breadth first search proceeds by exploring edges in the graph to find all the vertices in \(G\) for which there is a path from \(s\text{.}\) The remarkable thing about a breadth-first search is that it finds all the vertices that are a distance \(k\) from \(s\) before it finds any vertices that are a distance \(k+1\text{.}\) One good way to visualize what the breadth-first search algorithm does is to imagine that it is building a tree, one level of the tree at a time. A breadth first search adds all children of the starting vertex before it begins to discover any of the grandchildren.

To keep track of its progress, BFS colors each of the vertices white, gray, or black. All the vertices are initialized to white when they are constructed. A white vertex is an undiscovered vertex. When a vertex is initially discovered it is colored gray, and when BFS has completely explored a vertex it is colored black. This means that once a vertex is colored black, it has no white vertices adjacent to it. A gray node, on the other hand, may have some white vertices adjacent to it, indicating that there are still additional vertices to explore.

The BFS algorithm uses an extended version of the Vertex class that adds three new instance variables: distance (how far this vertex is from a starting point), previous (the previous Vertex in the search), and color. Each of these instance variables also has the appropriate getter and setter methods.

While we could use a String to represent the vertex color, we will instead use a Java enum class. An enum is “is a special data type that enables for a variable to be a set of predefined constants” (as defined in the Java Tutorials

docs.oracle.com/javase/tutorial/java/javaOO/enum.html

. The code for this class, which goes into a file named VertexColor.java, follows:

enum VertexColor {
    WHITE, GRAY, BLACK
}

Listing 7.9.1. The VertexColor Enumeration

The breadth-first search algorithm shown in Listing 7.9.2 below uses the adjacency list graph representation we developed earlier. In addition it uses a Queue, a crucial point as we will see, to decide which vertex to explore next.

  public void bfs(Vertex<T> start) {
    start.color = VertexColor.GRAY;
    start.distance = 0;
    start.previous = null;

    Queue<Vertex<T>> vertexQueue = new Queue<>();
    vertexQueue.enqueue(start);
    while (vertexQueue.size() > 0) {
        Vertex<T> current = vertexQueue.dequeue();
        for (Vertex<T> neighbor: current.getNeighbors()) {
            if (neighbor.color == VertexColor.WHITE) {
                neighbor.color = VertexColor.GRAY;
                neighbor.previous = current;
                neighbor.distance = current.distance + 1;
                vertexQueue.enqueue(neighbor);
            }
        }

        current.color = VertexColor.BLACK;
    }
}

Listing 7.9.2. Breadth-First Search

BFS begins at the starting vertex start and paints it gray to show that it is currently being explored. Two other values, the distance and the previous, are initialized to 0 and None respectively for the starting vertex. Finally, start is placed on a Queue (lines 6–7).

The next step is to begin to systematically explore vertices at the front of the queue. We explore each new node at the front of the queue by iterating over its adjacency list. As each node on the adjacency list is examined, its color is checked. If it is white, the vertex is unexplored, and four things happen:

The new unexplored vertex neighbor is colored gray.
The predecessor of neighbor is set to the current node current.
The distance to neighbor is set to the distance to current + 1.
neighbor is added to the end of a queue. Adding neighbor to the end of the queue effectively schedules this node for further exploration, but not until all the other vertices on the adjacency list of current have been explored.

After the current node’s neighbors have been explored, we color the node black (line 19) to mark that it has been fully explored.

Let’s look at how the bfs method would construct the breadth-first tree corresponding to the graph in Section 7.8. Starting from FOOL we take all nodes that are adjacent to FOOL and add them to the tree. The adjacent nodes include POOL, FOIL, FOUL, and COOL. Each of these nodes are added to the queue of new nodes to expand. Figure 7.9.3 shows the state of the in-progress tree along with the queue after this step.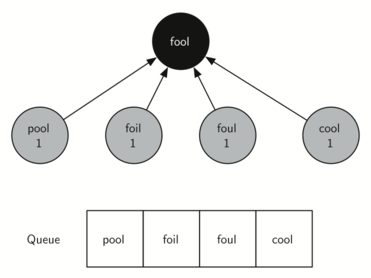

Figure 7.9.3. The First Step in the Breadth-First Search

In the next step bfs removes the next node (POOL) from the front of the queue and repeats the process for all of its adjacent nodes. However, when bfs examines the node COOL, it finds that the color of COOL has already been changed to gray. This indicates that there is a shorter path to COOL and that COOL is already on the queue for further expansion. The only new node added to the queue while examining POOL is POLL. The new state of the tree and queue is shown in Figure 7.9.4.

Figure 7.9.4. The Second Step in the Breadth-First Search

The next vertex on the queue is FOIL. The only new node that FOIL can add to the tree is FAIL. As bfs continues to process the queue, neither of the next two nodes adds anything new to the queue or the tree. Figure 7.9.5 shows the tree and the queue after expanding all the vertices on the second level of the tree.

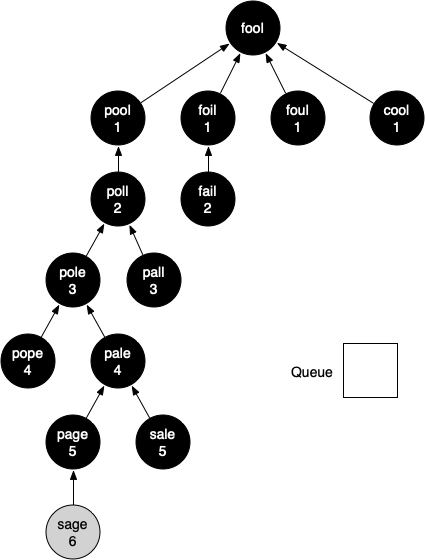
Figure 7.9.5. Breadth-First Search Tree After Completing One Level

Figure 7.9.6. Final Breadth-First Search Tree

You should continue to work through the algorithm on your own so that you are comfortable with how it works. Figure 7.9.6 shows the final breadth-first search tree after all the vertices in Section 7.8 have been expanded. The amazing thing about the breadth-first search solution is that we have not only solved the FOOL–SAGE problem we started out with, but we have solved many other problems along the way. We can start at any vertex in the breadth-first search tree and follow the predecessor arrows back to the root to find the shortest word ladder from any word back to FOOL. The method below (Listing 7.9.7) shows how to follow the predecessor links to print out the word ladder.

public static void traverse(Vertex<String> start) {
    Vertex<String> current = start;
    while (current != null) {
        System.out.println(current.key);
        current = current.previous;
    }
}

Listing 7.9.7.

Listing 7.9.8 shows a main method for testing the preceding code:

public static void main(String[] args) {
    WordLadder ladder = new WordLadder();
    Graph<String> wordGraph = ladder.buildGraph("wordlist.txt");

    String startWord = "fool";
    String endWord = "sage";

    /*
     * Because traverse uses the previous reference,
     * we reverse end and start words here.
     */
    wordGraph.bfs(wordGraph.getVertex(endWord));
    traverse(wordGraph.getVertex(startWord));
}

Listing 7.9.8.

With this output (using the full word list):

fool
pool
poll
pole
sole
sale
sage

You have attempted of activities on this page.

Prev Top Next