Section 8.3 Recursion Revisited
One of the most common uses of numerical computing today is in the field of cryptography. Each time you check your bank account, sign on to a secure website to purchase something, or sign on to your computer, you are using cryptography. In a general sense, cryptography is concerned with encrypting and decrypting information that you do not want other people to see. In this section we will look at some functions that are used in everyday cryptographic programming. In practice there may be faster ways to implement these functions, but each of them has an interesting recursive implementation.
The algorithms in this section make use of Java’s modulo operator (%). Remember that \(a \% b\) is what is left over after \(a\) is divided by \(b\text{,}\) for example \(10 \% 7 = 3\text{.}\) When we compute the result of any mathematical expression modulo 10, the only possible results are 0–9.
One of the earliest forms of cryptography used only simple modular arithmetic. Take the string
"uryybjbeyq", for example. Can you guess what message is encrypted? Listing 8.3.1 shows you the function that produced the message. Look at the listing and see if you can figure it out.public class ROT13 {
public static String encrypt(String message) {
String alphabet = "abcdefghijklmnopqrstuvwxyz";
String result = "";
for (int i = 0; i < message.length(); i++) {
int position = alphabet.indexOf(message.charAt(i));
if (position >= 0) {
result = result + alphabet.charAt((position + 13) % 26);
} else {
result = result + message.charAt(i);
}
}
return result;
}
public static void main(String [] args) {
String test = "let us encrypt this.";
String encrypted = encrypt(test);
System.out.println(encrypted);
String decrypted = encrypt("encrypted");
System.out.println(decrypted);
System.out.println(encrypt("uryybjbeyq");
}
}
The
encrypt function illustrates a form of encryption known as the Caesar Cipher. It also goes by the name ROT13, which is a bit more descriptive. encrypt simply takes each letter in the message and adds 13 to its ordinal position in the alphabet. If the position goes past the end of the alphabet, it wraps around. This wraparound function is easily accomplished using the modulo operator. In addition, since there are 26 letters in the alphabet, this function is symmetric. The symmetry allows us to use the function to encrypt and decrypt the same message. If you pass the string "uryybjbeyg" to the encrypt function, it returns "helloworld".Rotations by amounts other than 13 are possible; however, they are not symmetric with respect to encrypting and decrypting. Asymmetry would require us to write a separate decryption algorithm that subtracts the amount to rotate. In that case, we could generalize both the
encrypt and decrypt functions to take the amount of rotation as a parameter. In cryptographic terms, the rotation parameter is called the key and would be the number of positions to rotate. Given the message and the key, the encryption and decryption algorithms can do their jobs. Listing 8.3.2 shows the decryption algorithm that takes the amount of rotation as a parameter. As an exercise you should be able to modify Listing 8.3.2 to accept a parameter that specifies a key. public static String decrypt(String message, int key) {
String alphabet = "abcdefghijklmnopqrstuvwxyz";
String result = "";
for (int i = 0; i < message.length(); i++) {
int position = alphabet.indexOf(message.charAt(i));
if (position >= 0) {
result = result +
alphabet.charAt((position + 26 - key) % 26);
} else {
result = result + message.charAt(i);
}
}
return result;
}
Even if you keep the number
key from everyone except the person you are sending the message to, this simple form of encryption is not going to stop anyone from stealing your secrets for very long. In the remainder of this section, we will build up to a much more secure form of encryption, the RSA public key encryption algorithm.Subsection 8.3.1 Modular Arithmetic Theorems
If two numbers, \(a\) and \(b\text{,}\) give the same remainder when divided by \(n\text{,}\) we say that \(a\) and \(b\) are “congruent modulo \(n\text{.}\)” In shorthand we write \(a \equiv~b~\pmod{n}\text{.}\) The algorithms in this section make use of three important theorems:
- If \(a \equiv b \pmod{n}\) then \(\forall c, a + c \equiv b + c \pmod{n}\text{.}\)
- If \(a \equiv b \pmod{n}\) then \(\forall c, ac \equiv bc \pmod{n}\text{.}\)
- If \(a \equiv b \pmod{n}\) then \(\forall p, p > 0, a^p \equiv b^p \pmod{n}\text{.}\)
Subsection 8.3.2 Modular Exponentiation
Suppose we wanted to know the last digit of \(3^{1,254,906}\text{.}\) Not only is that a large computation problem, but using Java’s arbitrary-precision integers (the
BigInteger class), the number has 598,743 digits! All we want to know is the value of the rightmost digit. There are really two problems here. First, how do we compute \(x^n\) efficiently? Second, how can we compute \(x^n \pmod{p}\) without first calculating all 598,743 digits and then looking at the last one?The answer to the second question is easy, given the third theorem from above.
- Initialize result to 1.
-
Repeat \(n\) times:
- Multiply result by \(x\text{.}\)
- Apply modulo operation to result.
The above approach makes the computation simpler because we are keeping the result smaller rather than following it out to its full precision. However, we can do even better using a recursive approach.
\begin{equation*}
x^n =
\begin{cases}
(x \cdot x)^{ n/2 } & \text{if is even} \\
(x \cdot x^{n-1}) = x \cdot (x \cdot x)^{\lfloor n/2 \rfloor} & \text{if is odd}
\end{cases}
\label{eqn:pow}
\end{equation*}
Remember that for a floating point number \(n\text{,}\) the floor operation \(\lfloor n \rfloor\) results in the largest integer smaller than \(n\text{.}\) Java’s integer division returns the floor of the result of the division, so we do not need to do anything special in our code to achieve the results we want. The above equation gives us a very nice recursive definition for computing \(x^n\text{.}\) All we need now is a base case. Recall that for any number \(x\text{,}\) \(x^0 = 1\text{.}\) Since we are reducing the size of our exponent in each recursive call, checking for the condition \(n = 0\) is a good base case.
public static int modExp(int x, int n, int p) {
if (n == 0) {
return 1;
}
int t = (x * x) % p;
int result = modExp(t, n / 2, p);
if (n % 2 != 0) {
result = (result * x) % p;
}
return result;
}
Notice that in the above equation both the even and odd cases include a factor of \((x \cdot x)^{\lfloor n/2 \rfloor}\text{,}\) so we compute that unconditionally and store it in the variable
t. Also note that since we are computing modulo p we still apply the modulo operator at each step of the calculation. The solution in Listing 8.3.3 keeps the result size small and uses many fewer multiplications than a purely iterative approach. (For \(3^{1,254,906}\text{,}\) there are only 22 multiplications.)Subsection 8.3.3 The Greatest Common Divisor and Multiplicative Inverses
A multiplicative inverse of a positive integer \(x\) modulo \(m\) is any number \(a\) such that \(ax \equiv 1 \pmod{m}\text{.}\) For example, let \(x = 3\text{,}\) \(m = 7\text{,}\) and \(a = 5\text{;}\) \(3 \times 5 = 15\) and \(15\ \%\ 7 = 1\text{,}\) so 5 is a multiplicative inverse of 3 modulo 7.
The idea of multiplicative inverses in the world of modulo arithmetic may seem very confusing at first. How did we select 5 in the previous example? Is 5 the only multiplicative inverse of 3 modulo 7? Do all numbers \(a\) have a multiplicative inverse for any given \(m\text{?}\)
Let’s look at an example that may shed some light on the first question: how did we select 5 as the multiplicative inverse of 3 modulo 7? Look at the following jshell session:
jshell> for (int i = 1; i < 40; i++) {
...> if ((3 * i) % 7 == 1) {
...> System.out.println(i);
...> }
...> }
5
12
19
26
33
This little experiment tells us that there are many multiplicative inverses (modulo 7) for \(x=3\) and \(m = 7\text{,}\) namely \(5, 12, 19, 26, 33\text{,}\) and so on. Do you notice anything interesting about the sequence? Each number in the sequence is two less than a multiple of seven.
Do all pairs of numbers \(x\) and \(m\) have a multiplicative inverse? Let’s look at another example. Consider \(x=4\) and \(m=8\text{.}\) Plugging 4 and 8 into the loop in the previous example gives us no output. If we take out the conditional and print out the results of \((4 \cdot i)\ \%\ 8\text{,}\) we get the sequence \((0, 4, 0, 4, 0, 4\dots\)). Here we have a case where the remainder alternates between 0 and 4 repeatedly. Clearly the result is never going to be 1. How can we know that ahead of time?
The answer is that a number \(x\) has a multiplicative inverse, modulo \(m\text{,}\) if and only if \(m\) and \(x\) are relatively prime. Two numbers are relatively prime if \(gcd(m, x) = 1\text{.}\) Recall that the greatest common divisor (GCD) is the largest integer that divides both numbers. The next question is how can we compute the greatest common divisor for a pair of numbers?
Given two numbers \(a\) and \(b\) we can find the GCD by repeatedly subtracting \(b\) from \(a\) until \(a < b\text{.}\) When \(a < b\text{,}\) we switch roles for \(a\) and \(b\text{.}\) At some point \(a - b\) becomes 0, so we swap \(a\) and \(b\) one more time. At that point we have \(gcd(a, 0) = a\text{.}\) This algorithm was first described more than 2,000 years ago and is called Euclid’s algorithm.
In terms of recursive algorithm design, Euclid’s algorithm is very straightforward. The base case is when \(b = 0\text{.}\) There are two possibilities for a recursive call: when \(a < b\text{,}\) we swap \(a\) and \(b\) and make a recursive call. Otherwise, we can make a recursive call passing \(a - b\) in place of \(a\text{.}\) Euclid’s algorithm is shown in Listing 8.3.4.
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
else if (a < b) {
return gcd(b, a);
}
return gcd(a - b, b);
}
Although Euclid’s algorithm is quite easy to understand and program, it is not as efficient as we would like, particularly if \(a >> b\text{.}\) Once again, modular arithmetic comes to our rescue. Notice that the result of the last subtraction (when \(a - b < b\)) is really the same as the remainder of \(a\) divided by \(b\text{.}\) With that in mind, we can cut out all of the subtractions and combine the swap of \(a\) and \(b\) in one recursive call. A revised algorithm is shown in Listing Listing 8.3.5.
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
Now that we have a way to know whether two numbers \(x\) and \(m\) will have a multiplicative inverse, our next task is to write an efficient algorithm to compute the inverse. Suppose that for any pair of numbers \(x\) and \(y\) we could compute both \(gcd(x,y)\) and a pair of integers \(a\) and \(b\) such that \(d = gcd(x, y) = ax + by\text{.}\) For example, \(1 = gcd(3, 7) = -2 \times 3 + 1 \times 7\text{,}\) so here \(a = -2\) and \(b = 1\) are possible values for \(a\) and \(b\text{.}\)
Rather than any numbers \(x\) and \(y\text{,}\) let’s use \(m\) and \(x\) from our previous examples. Now we have \(1 = gcd(m, x) = am + bx\text{.}\) From the discussion at the beginning of this section we know that \(bx = 1 \mod{m}\text{,}\) so \(b\) is a multiplicative inverse of \(x\) modulo \(m\text{.}\)
We have reduced the problem of computing inverses to the problem of finding integers \(a\) and \(b\) that satisfy the equation \(d = gcd(x, y) = ax + by\text{.}\) Since we started this problem with the GCD algorithm, we can finish it with an extension of this algorithm as well. We will take two numbers \(x >= y\) and return an array of three numbers \([d, a, b]\) such that \(d = gcd(x, y)\) and \(d = ax + by\text{.}\) The extension to Euclid’s algorithm is shown in Listing 8.3.6.
public static int[] extGcd(int x, int y) {
if (y == 0) {
return(new int[] {x, 1, 0});
} else {
int[] info = extGcd(y, x % y);
int d = info[0];
int a = info[1];
int b = info[2];
return(new int[] {d, b, a - (x / y) * b});
}
}
Notice that when we get the base case \(y = 0\text{,}\) we return \(d = x\) just like the original Euclid’s algorithm. However, we return two additional values \(a =1\) and \(b = 0\text{.}\) Together these three values satisfy the equation \(d = ax + by\text{.}\) If \(y > 0\text{,}\) then we recursively compute values \((d, a, b)\) such that \(d = gcd(y, x \mod{y})\) and \(d = ay + b(x \mod{y})\text{.}\) As with the original algorithm, \(d = gcd(x, y)\text{.}\) But what about the other two values, \(a\) and \(b\text{?}\) We know that \(a\) and \(b\) must be integers, so let’s call them \(A\) and \(B\text{.}\) Further, we know that \(d = Ax + By\text{.}\) To figure out what \(A\) and \(B\) should be, let’s rearrange the equation as follows:
\begin{equation*}
\begin{aligned}
d = & ay + b(x \mod{y}) \\
= & ay + b(x - \lfloor x / y \rfloor y) \\
= & bx + (a - \lfloor x / y \rfloor b)y\end{aligned}
\end{equation*}
Note the substitution made in the second line, \(x \mod{y} = x - \lfloor x / y \rfloor\text{.}\) This is legal because this is how we would normally calculate the remainder of x / y (\(x \mod{y}\)). Looking at the rearranged equation, we can see that \(A = b\) and \(B = a - \lfloor x / y \rfloor b\text{.}\) Notice that this is exactly what the expression in the
return in Listing 8.3.6 does! To check this, note that at each return step in the algorithm the return values satisfy the equation \(d = ax + by\text{.}\) To understand how our extended GCD algorithm works, let’s start with an example: let \(x = 25\) and \(y = 9\text{.}\) Figure 8.3.7 illustrates the call and return values for the recursive function.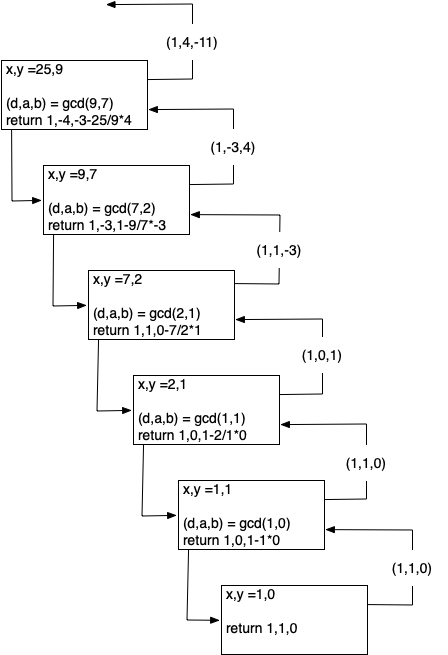
Subsection 8.3.4 RSA Algorithm
Now we have all the tools we need to write the RSA encryption algorithm. The RSA algorithm (named after the people who first publicly described it: Rivest, Shamir, and Adleman) is perhaps the easiest to understand of all the public key encryption algorithms. Public key cryptography was invented by Whitfield Diffie and Martin Hellman and independently by Ralph Merkle. The major contribution of public key cryptography was the idea that keys could come in pairs: an encryption key to convert the plaintext message to ciphertext, and a decryption key to convert the ciphertext back to plaintext. The keys only work one way so that a message encrypted with the private key can only be decrypted with the public key, and vice versa.
RSA gets its security from the difficulty of factoring large numbers. The public and private keys are derived from a pair of large (100–200 digit) prime numbers. Since long integers are native to Python, this is a fun and easy algorithm to implement.
To generate the two keys, choose two large prime numbers \(p\) and \(q\text{.}\) Then compute the product
\begin{equation*}
n = p \times q
\end{equation*}
The next step is to randomly choose the encryption key \(e\) such that \(e\) and \((p - 1) \times (q - 1)\) are relatively prime; that is
\begin{equation*}
gcd(e, (p - 1) \times (q-1)) = 1
\end{equation*}
Finally, the decryption key \(d\) is simply the multiplicative inverse of \(e\) modulo \((p - 1) \times (q - 1)\text{.}\) For this we can use our extended version of Euclid’s algorithm.
The numbers \(e\) and \(n\) taken together are the public key. The number \(d\) is the private key. Once we have computed \(n, e\text{,}\) and \(d\text{,}\) the original primes \(p\) and \(q\) are no longer needed. However, they should not be revealed.
To encrypt a message we simply use the equation \(c = m^e \pmod{n}\text{.}\) To decrypt the message we use \(m = c^d \pmod{n}\text{.}\)
It is easy to see that this works when you remember that \(d\) is the multiplicative inverse of \(e \pmod{n}\text{.}\)
\begin{equation*}
\begin{aligned}
c^d & = (m^e)^d \pmod{n} \\
& = m^{ed} \pmod{n} \\
& = m^1 \pmod{n} \\
& = m \pmod{n} \end{aligned}
\end{equation*}
Before we turn all these equations into Python code, we need to talk about a couple of other details. First, how do we take a text message like “hello world” and turn it into a number? The easiest way is to simply use the ASCII values associated with each character and concatenate all the numbers together. However, since the decimal versions of the numbers of the ASCII values vary in the number of digits needed to represent them, we will use the hexadecimal numbers where we know very reliably that two hexadecimal digits represent a single byte or character.
| h | e | l | l | o | w | o | r | l | d | |
| 104 | 101 | 108 | 108 | 111 | 32 | 119 | 111 | 114 | 108 | 100 |
| 68 | 65 | 6c | 6c | 6f | 20 | 77 | 6f | 72 | 6c | 64 |
Putting all the hexadecimal digits together we could convert that large hex number into a decimal integer:
\begin{equation*}
m = 126207244316550804821666916
\end{equation*}
Java can handle this large number just fine via the
BigInteger class. However, there are two reasons that real programs using RSA encryption break the message up into smaller chunks and encrypt each chunk. The first reason is performance. Even a relatively short email message, say 1k of text, will generate a number with 2,000 to 3,000 digits! If we raise that to a power of \(d\) which has 10 digits, we are talking about a very long number indeed.The second reason for breaking the message into chunks is the restriction that \(m \le n\text{.}\) We must be sure that the message has a unique representation modulo \(n\text{.}\) With binary data, choose the largest power of two that is less than \(n\text{.}\) For example, let’s choose \(p\) and \(q\) to be 5563 and 8191. So \(n = 5563 \times 8191 = 45,566,533\text{.}\) To keep the integer value of our chunks less than \(m\text{,}\) we will divide up our word into chunks that use less than the number of bytes needed to represent \(n\text{.}\) In Java, we can use the
BigInteger.bitLength() method to find this value. Given the number of bits needed to represent a number, we can divide by eight to find the number of bytes. Since each character in the message can be represented by a single byte, this division tells us the number of bytes we can put in each chunk. Conveniently, this lets us simply break the message up into chunks of \(n\) characters and convert the hexadecimal representation of each chunk into an integer. For this example we can represent \(45,566,533\) using 26 bits. Using integer division and dividing by eight tells us that we should break our message into chunks of three characters.The characters “h,” “e,” and “l” have the hexadecimal values of \(68\text{,}\) \(65\text{,}\) and \(6c\text{,}\) respectively. Concatenating those together gives us \(68656c\) and converting that to a decimal gives us \(6841708\text{.}\)
| \(m_1 = 6841708\) | \(m_2 = 7106336\) | \(m_3 = 7827314\) | \(m_4 = 27748\) |
Note that breaking the message into chunks can be very tricky, in particular when the result of applying the RSA transformation to a chunk produces a number that is less than seven digits long. In this case we need to be careful to add a leading zero to the result when we glue our chunks back together again. You can see how this might happen in \(m_1\) and \(m_4\) above.
Now let’s choose a value for \(e\text{.}\) We can select values randomly and use the GCD algorithm to test them against \((p - 1) \times (q - 1) = 45552780\text{.}\) Remember that we are looking for an \(e\) that is relatively prime to 45,552,780. The number 1,471 will work nicely for this example.
\begin{equation*}
\begin{aligned}
d & = extGcd(45552780, 1471) \\
& = -11705609 \\
& = 45552780-11705609 \\
& = 33847171\end{aligned}
\end{equation*}
Let’s use this information to encrypt the first chunk of our message:
\begin{equation*}
c = 6841708^{1471} \pmod{45566533} = 16310024
\end{equation*}
To check our work, let’s decrypt \(c\) to make sure we recover the original value:
\begin{equation*}
m = 16310024^{33847171} \pmod{45566533} = 6841708
\end{equation*}
The remaining chunks of the message can be encrypted using the same procedure and sent all together as the encrypted message.
Finally, let’s look at three Java methods.
genKeyscreates a public and private key, given \(p\) and \(q\text{.}\)encrypttakes a message, the public key, and \(n\) and returns an encrypted version of the message.decrypttakes the encrypted message, the private key, and \(n\) and returns the original message.
public static long[] genKeys(long p, long q) {
long n = p * q;
long m = (p - 1) * (q - 1);
long encryptKey = (long) (Math.random() * n);
while (gcd(m, encryptKey) != 1) {
encryptKey = (long) (Math.random() * n);
}
long[] dab = extGcd(m, encryptKey);
long decryptKey = dab[0];
long a = dab[1];
long b = dab[2];
if (b < 0) {
decryptKey = m + b;
} else {
decryptKey = b;
}
return new long[]{encryptKey, decryptKey, n};
}
public static long[] encrypt(String msg, long encryptKey,
long n) {
BigInteger bigN = new BigInteger(Long.toString(n));
int chunkSize = bigN.bitLength() / 8;
long [] allChunks = strToChunks(msg, chunkSize);
for (int i = 0; i < allChunks.length; i++) {
allChunks[i] = modExp(allChunks[i], encryptKey, n);
}
return allChunks;
}
public static String decrypt(long[] cipherChunks, long decryptKey,
long n) {
BigInteger bigN = new BigInteger(Long.toString(n));
int chunkSize = bigN.bitLength() / 8;
long[] plainChunks = new long[cipherChunks.length];
for (int i = 0; i < cipherChunks.length; i++) {
plainChunks[i] = modExp(cipherChunks[i], decryptKey,
n);
}
return chunksToStr(plainChunks, chunkSize);
}
Here is a jshell session that uses these functions to create public and private keys, encrypt, and decrypt as we did in the example above. The array
edn contains the encryption key, decryption key, and the product of the prime numbers (n).jshell> import rsa.TestRSA
jshell> TestRSA test = new TestRSA();
test ==> rsa.TestRSA@3941a79c
jshell> String msg = "Java and RSA";
msg ==> "Java and RSA"
jshell> long [] edn = test.genKeys(5563, 8191);
edn ==> long[3] { 19157743, 22783087, 45566533 }
jshell> long [] encrypted = test.encrypt(msg, edn[0], edn[2]);
encrypted ==> long[4] { 8033810, 24305963, 24092116, 40127463 }
jshell> String decrypted = test.decrypt(encrypted, edn[1], edn[2]);
decrypted ==> "Java and RSA"
The last thing to look at is the two helper functions that break our string into chunks and merge chunks into a string (Listing 8.3.10). These functions make use of Java
byte objects, which allow us to store any string as a sequence of bytes.public long[] strToChunks(String msg, int chunkSize) {
byte[] msgBytes;
msgBytes = msg.getBytes();
int numChunks = (msgBytes.length + chunkSize - 1) / chunkSize;
long[] chunkList = new long[numChunks];
int n = 0;
String hex = "";
for (int i = 0; i < msgBytes.length; i++) {
hex += String.format("%02x", msgBytes[i]);
if (i % chunkSize == chunkSize - 1) {
chunkList[n] = Long.parseLong(hex, 16);
n++;
hex = "";
}
}
if (!hex.equals("")) {
hex = hex + "00".repeat(chunkSize - hex.length() / 2);
chunkList[n] = Long.parseLong(hex, 16);
}
return chunkList;
}
public String chunksToStr(long[] chunkList, int chunkSize) {
byte[] byteArr = new byte[chunkList.length * chunkSize];
int n = 0;
for (long chunk: chunkList) {
for (int i = 0; i < chunkSize; i++) {
byteArr[n + (chunkSize - i - 1)] =
(byte) ((chunk >> (i * 8)) & 0xff);
}
n += chunkSize;
}
return new String(byteArr);
}
In Listing 8.3.10 we see the procedure for turning a string into a list of chunks. One important thing to note is that we must always make sure that our hexadecimal number corresponds to a character that is exactly two digits long. We can do this by using the string formatting expression
%02x in line 11.The loop in lines 10–17 creates a hex string of the given chunk size and converts it to a
Long integer. The code in lines 18–21 make sure that any remaining hex bytes go into the last chunk.Transforming the decrypted chunks back to a string works by taking each decrypted chunk and moving its bytes into a byte array. This occurs in lines 30 and 31. The
>> shifts the chunk to the right by the number of bits given on the right side of the operator. We keep only the last eight bits of the shifted value by doing a bitwise and (the & operator) with eight 1-bits, which works out to hexadecimal 0xff. The loop shifts 0 bits, then 8, then 16, etc. This extracts bytes from right to left. That is why line 30 has the subtraction to put the resulting bytes into the byte array in left to right order.In line 35, we use a
String constructor to convert the byte array to a string.You have attempted of activities on this page.

