Section 4.3 Calculating the Sum of an Array of Numbers
We will begin our investigation with a problem that you already know how to solve without using recursion. Suppose that you want to calculate the sum of an array of numbers such as: \([1, 3, 5, 7, 9]\text{.}\) An iterative method that computes the sum is shown in Listing 4.3.1. The method uses an accumulator variable (
theSum) to compute a running total of all the numbers in the array by starting with \(0\) and adding each number in the array.Pretend for a minute that you do not have
while loops or for loops. How would you compute the sum of an array of numbers? If you were a mathematician you might start by recalling that addition is a function that is defined for two operands, a pair of numbers. To redefine the problem from adding an array to adding pairs of numbers, we could rewrite the array sum as a fully parenthesized expression. Such an expression looks like this:
\begin{equation*}
((((1 + 3) + 5) + 7) + 9)
\end{equation*}
We can also parenthesize the expression the other way around,
\begin{equation*}
(1 + (3 + (5 + (7 + 9))))
\end{equation*}
Notice that the innermost set of parentheses, \((7 + 9)\text{,}\) is a problem that we can solve without a loop or any special constructs. In fact, we can use the following sequence of simplifications to compute a final sum.
\begin{align*}
total = \ (1 + (3 + (5 + (7 + 9))))\amp\\
total = \ (1 + (3 + (5 + 16)))\amp\\
total = \ (1 + (3 + 21))\amp\\
total = \ (1 + 24)\amp\\
total = \ 25\amp
\end{align*}
How can we take this idea and turn it into a Java program? First, let’s restate the sum problem in terms of Java arrays. In pseudo-Java notation we might say the sum of the list
numArray is the sum of the first element of the list (numArray[0]) and the sum of the numbers in the rest of the list (numArray[1...)]). To state it in a functional form:
\begin{equation*}
arraySum(numArray) = first(numArray) + arraySum(rest(numArray))
\label{eqn:arraySum}
\end{equation*}
In this equation \(first(numArray)\) returns the first element of the list and \(rest(numArray)\) returns a list of everything but the first element. We can use the
copyOfRange method in the java.util.Arrays class to make a copy of the “rest of the list”: Listing 4.3.2. 1
There are a few key ideas in this listing to look at. First, on line 5 we are checking to see if the list is one element long. This check is crucial and is our escape clause from the method. The sum of an array of length 1 is trivial; it is just the number in the array. Second, on line 9 our metho calls itself! This is the reason that we call the
arraySum algorithm recursive. A recursive method is a method that calls itself.
Figure 4.3.3 shows the series of recursive calls that are needed to sum the array \([1, 3, 5, 7, 9]\text{.}\) You should think of this series of calls as a series of simplifications. Each time we make a recursive call we are solving a smaller problem, until we reach the point where the problem cannot get any smaller.
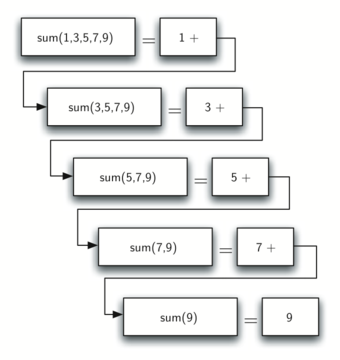
When we reach the point where the problem is as simple as it can get, we begin to piece together the solutions of each of the small problems until the initial problem is solved. Figure 4.3.4 shows the additions that are performed as
arraySum works its way backward through the series of calls, returning its result to the caller. When arraySum returns from the topmost problem, we have the solution to the whole problem.
You have attempted of activities on this page.
