Section 6.17 AVL Tree Performance
Before we proceed any further let’s look at the result of enforcing this new balance factor requirement. Our claim is that by ensuring that a tree always has a balance factor of -1, 0, or 1 we can get better Big-O performance of key operations. Let us start by thinking about how this balance condition changes the worst-case tree. There are two possibilities to consider, a left-heavy tree and a right-heavy tree. If we consider trees of heights 0, 1, 2, and 3, Figure 6.17.1 illustrates the most unbalanced left-heavy tree possible under the new rules.
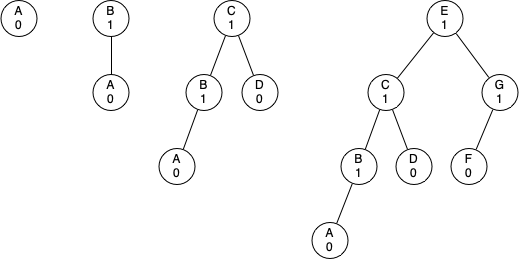
Looking at the total number of nodes in the tree we see that for a tree of height 0 there is 1 node, for a tree of height 1 there is \(1 + 1
= 2\) nodes, for a tree of height 2 there are \(1 + 1 + 2 = 4\text{,}\) and for a tree of height 3 there are \(1 + 2 + 4 = 7\text{.}\) More generally the pattern we see for the number of nodes in a tree of height \(h\) (\(N_h\)) is:
\begin{equation*}
N_h = 1 + N_{h-1} + N_{h-2}
\end{equation*}
This recurrence may look familiar to you because it is very similar to the Fibonacci sequence. We can use this fact to derive a formula for the height of an AVL tree given the number of nodes in the tree. Recall that for the Fibonacci sequence the \(i^{th}\) Fibonacci number is given by:
\begin{align*}
F_0 & = 0\\
F_1 & = 1\\
F_i & = F_{i-1} + F_{i-2} \text{ for all } i \ge 2
\end{align*}
An important mathematical result is that as the numbers of the Fibonacci sequence get larger and larger the ratio of \(F_i / F_{i-1}\) becomes closer and closer to approximating the golden ratio \(\Phi\) which is defined as \(\Phi = \frac{1 + \sqrt{5}}{2}\text{.}\) You can consult a math text if you want to see a derivation of the previous equation. We will simply use this equation to approximate \(F_i\) as \(F_i =
\Phi^i/\sqrt{5}\text{.}\) If we make use of this approximation we can rewrite the equation for \(N_h\) as:
\begin{equation*}
N_h = F_{h+3} - 1, h \ge 1
\end{equation*}
By replacing the Fibonacci reference with its golden ratio approximation we get:
\begin{equation*}
N_h = \frac{\Phi^{h+2}}{\sqrt{5}} - 1
\end{equation*}
If we rearrange the terms, take the base 2 log of both sides, and then solve for \(h\text{,}\) we get the following derivation:
\begin{align*}
\log{N_h+1} & = (h+2)\log{\Phi} - \frac{1}{2} \log{5}\\
& = \frac{\log{(N_h+1)} - 2 \log{\Phi} + \frac{1}{2} \log{5}}{\log{\Phi}}\\
h & = 1.44 \log{N_h}
\end{align*}
This derivation shows us that at any time the height of our AVL tree is equal to a constant (1.44) times the log of the number of nodes in the tree. This is great news for searching our AVL tree because it limits the search to \(O(\log{n})\text{.}\)
You have attempted of activities on this page.

