Section 7.8 Building the Word Ladder Graph
Our first problem is to figure out how to turn a large collection of words into a graph. What we would like is to have an edge from one word to another if the two words are only different by a single letter. If we can create such a graph, then any path from one word to another is a solution to the word ladder puzzle. Figure 7.8.1 shows a small graph of some words that solve the FOOL to SAGE word ladder problem. Notice that the graph is an undirected graph and that the edges are unweighted.
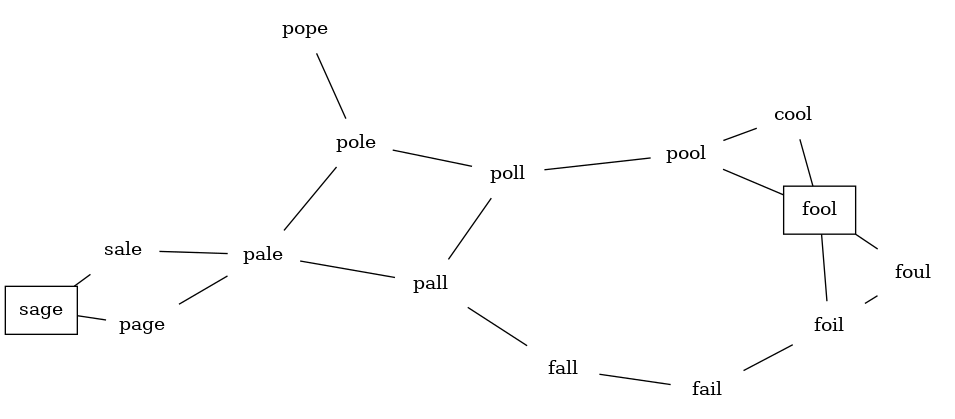
We could use several different approaches to create the graph we need to solve this problem. Let’s start with the assumption that we have a list of words that are all the same length. As a starting point, we can create a vertex in the graph for every word in the list. To figure out how to connect the words, we could compare each word in the list with every other. When we compare we are looking to see how many letters are different. If the two words in question are different by only one letter, we can create an edge between them in the graph. For a small set of words that approach would work fine; however, let’s suppose we have a list of 2,430 words. Roughly speaking, comparing one word to every other word on the list is an \(O(n^2)\) algorithm. For 2,430 words, \(n^2\) is almost 6 million comparisons.
We can do much better by using the approach shown in Figure 7.8.2. Suppose that we have a number of buckets, each labeled with a four-letter word, except that one of the letters on the label has been replaced by an underscore. As we process a list of words, we compare each word with each bucket using the underscore (_) as a wildcard. Every time we find a matching bucket we put the word in that bucket, so that both POPE and POPS would both go into the POP_ bucket. Once we have all the words in the appropriate buckets, we know that all the words in each bucket must be connected.

In Java, we can implement the scheme we have just described by using a HashMap. The labels on the buckets we have just described are the keys in our HashMap. The value stored for each key is a list of words that fit that label (thus, the bucket key POP_ would have POPE and POPS as its value). Once we have the HashMap built, we can create the graph. We start our graph by creating a vertex for each word in the graph. Then we create edges between all the vertices we find for words found under the same key in the HashMap. Listing 7.8.3 shows the Java code required to build the graph from a file containing one word per line.
public Graph<String> buildGraph(String fileName) {
Graph<String> wordGraph = new Graph<String>();
HashMap<String, Set<String>> buckets = new HashMap<>();
File inFile = new File(fileName);
try (Scanner input = new Scanner(inFile);) {
while (input.hasNextLine()) {
String line = input.nextLine();
String word = line.trim();
for (int i = 0; i < word.length(); i++) {
String bucket = word.substring(0, i) + "_" +
word.substring(i + 1);
if (!buckets.containsKey(bucket)) {
buckets.put(bucket, new HashSet<String>());
}
buckets.get(bucket).add(word);
}
}
int nEdges = 0;
for (Set<String> similarWords: buckets.values()) {
if (similarWords.size() > 1) {
for (String word1: similarWords) {
for (String word2: similarWords) {
if (!word1.equals(word2)) {
wordGraph.addEdge(word1, word2);
}
nEdges++;
}
}
}
}
}
catch (Exception ex) {
System.out.println(ex);
}
return wordGraph;
}
Let’s look at the preceding code in a bit more detail. First, building the buckets:
- In lines 9 and 10, we read in a word from the file.
- For each letter in the word (line 11), we create a bucket label (lines 12–13). For example, for the input word SAGE, the loop would create the labels _AGE, S_GE, SA_E, and SAG_ as it went through its iterations.
- If the bucket label doesn’t already exist, we add it to our HashMap (lines 14–16). Its value will be an empty
HashSet. - The word we are currently processing belongs to that bucket (line 17).
Once the buckets are available, we proceed to build the graph. The loop in line 21 gives us one bucket at a time. If the bucket has more than one word in it (line 22) we run a nested loop through all the pairs of words in the bucket (lines 23 and 24) adding edges between them (line 26) except for an edge from a word to itself (line 25). The
addEdge method will add vertices to the graph if they don’t already exist.Since this is our first real-world graph problem, you might be wondering how sparse the graph is. The list of four-letter words we have for this problem is 2,436 words long. If we were to use an adjacency matrix, the matrix would have \(2,436 \cdot 2,36\) = 5,934,096 cells. The graph constructed by the
buildGraph function has exactly 27,592 edges, so the matrix would have only 0.46% of the cells filled! That is a very sparse matrix indeed.You have attempted of activities on this page.

