Skip to main content
Logo image

Problem Solving with Algorithms and Data Structures using Java: The Interactive Edition

Bradley N. Miller, David L. Ranum, Roman Yasinovskyy, J. David Eisenberg

Section 6.6 Nodes and References

Our second method to represent a tree uses nodes and references. In this case we will define a class that has attributes for the root value as well as the left and right subtrees. Using nodes and references, we might think of the tree as being structured like the one shown in Figure 6.6.1. Since this representation more closely follows the object-oriented programming paradigm, we will continue to use this representation for the remainder of the chapter.
Figure 6.6.1. A Simple Tree Using a Nodes and References Approach
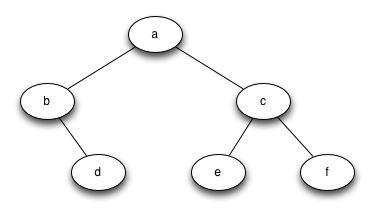
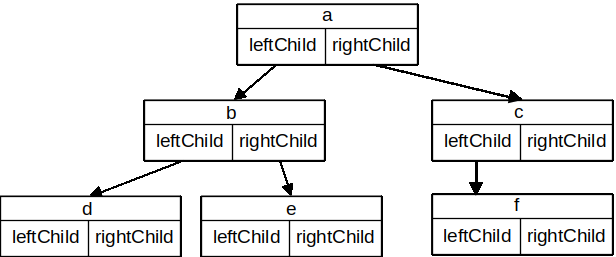
We will start out with a simple class definition for the nodes and references approach as shown in Listing 6.6.2. The important thing to remember about this representation is that the attributes leftChild and rightChild will become references to other instances of the BinaryTree class. For example, when we insert a new left child into the tree, we create another instance of BinaryTree and modify this.leftChild in the root to reference the new tree.
class BinaryTree<T> {
    T key;
    BinaryTree<T> leftChild;
    BinaryTree<T> rightChild;

    public BinaryTree(T rootObject) {
        this.key = rootObject;
        this.leftChild = null;
        this.rightChild = null;
    }
    // more code here..
}
Listing 6.6.2. Binary Tree Constructor
Notice that in Listing 6.6.2, the constructor expects to get some kind of object to store in the root. We will use generics so that our trees are not restricted to holding values of only one particular type. For our early examples, we will store the name of the node as the root value. Using nodes and references to represent the tree in Figure 6.6.1, we would create six instances of the BinaryTree class.
Next let’s look at the methods we need to build the tree beyond the root node. To add a left child to the tree, we will create a new binary tree object and set the leftChild attribute of the root to refer to this new object. The code for insertLeft is shown in Listing 6.6.3.
public void insertLeft(T newNode) {
    if (this.leftChild == null) {
        this.leftChild = new BinaryTree<T>(newNode);
    } else {
        BinaryTree<T> newChild = new BinaryTree<T>(newNode);
        newChild.leftChild = this.leftChild;
        this.leftChild = newChild;
    }
}
Listing 6.6.3.
We must consider two cases for insertion. The first case is characterized by a node with no existing left child. When there is no left child, we add a node to the tree. The second case is characterized by a node with an existing left child. In the second case, we insert a node and push the existing child down one level in the tree. The second case is handled by the else statement on line 4 of Listing 6.6.3.
The code for insertRight must consider a symmetric set of cases. There will either be no right child, or we must insert the node between the root and an existing right child. The insertion code is shown in Listing 6.6.4.
public void insertRight(T newNode) {
    if (this.rightChild == null) {
        this.rightChild = new BinaryTree<T>(newNode);
    } else {
        BinaryTree<T> newChild = new BinaryTree<T>(newNode);
        newChild.rightChild = this.rightChild;
        this.rightChild = newChild;
    }
}
Listing 6.6.4.
To round out the definition for a simple binary tree data structure, we will write accessor methods for the left and right children and for the root values (see Listing 6.6.5) .
public T getRootValue() {
    return this.key;
}

public void setRootValue(T value) {
    this.key = value;
}

public BinaryTree<T> getLeftChild() {
    return this.leftChild;
}

public BinaryTree<T> getRightChild() {
    return this.rightChild;
}
Listing 6.6.5.
Now that we have all the pieces to create and manipulate a binary tree, let’s use them to check on the structure a bit more. Let’s make a simple tree with node a as the root, and add nodes “b” and “c” as children. Listing 6.6.6 creates the tree and looks at the some of the values stored in key, leftChild, and rightChild. Notice that both the left and right children of the root are themselves distinct instances of the BinaryTree class. As we said in our original recursive definition for a tree, this allows us to treat any child of a binary tree as a binary tree itself.
Listing 6.6.6. Test Program for BinaryTree Class

Exercises Self Check

1.

Write a method named buildTree that returns a tree using the nodes and references implementation that looks like this:
You have attempted of activities on this page.
PrevTopNext