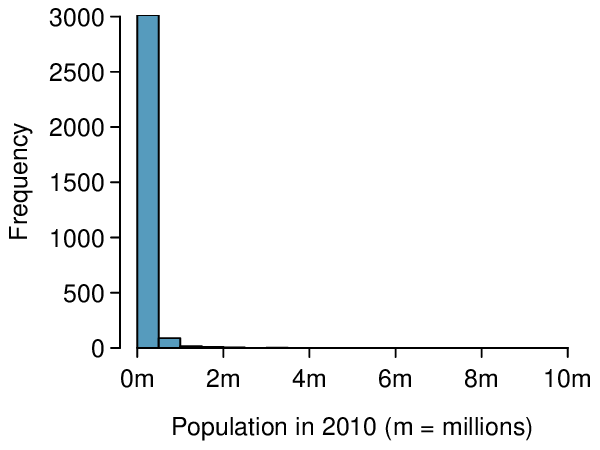
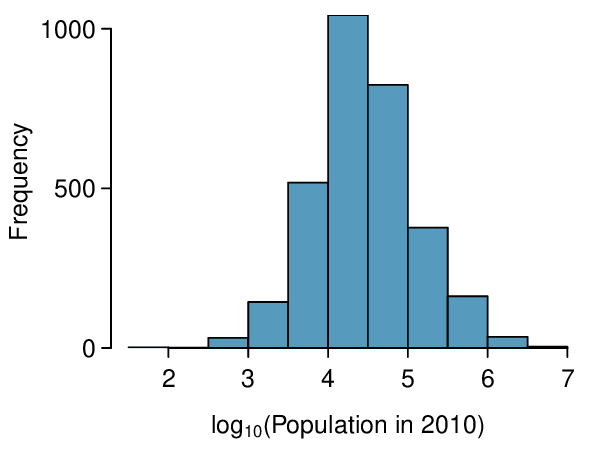
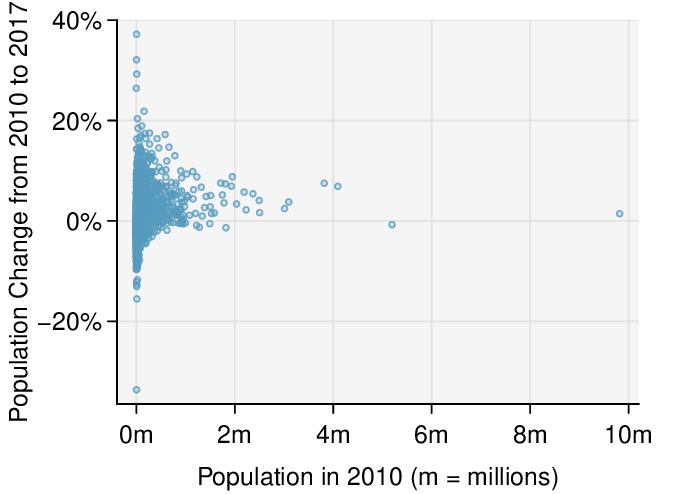
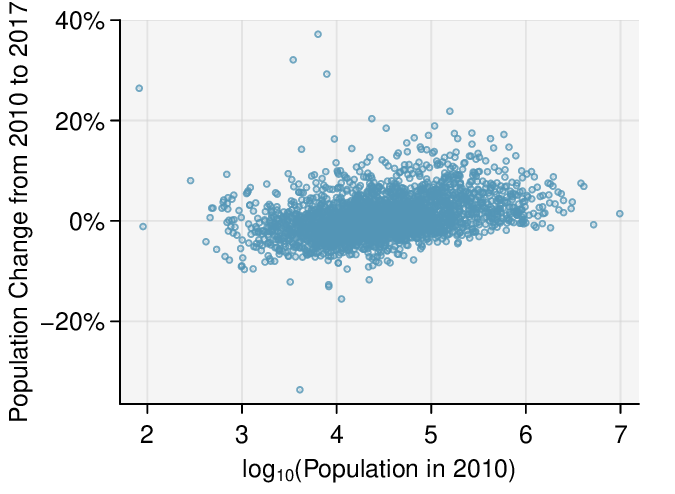
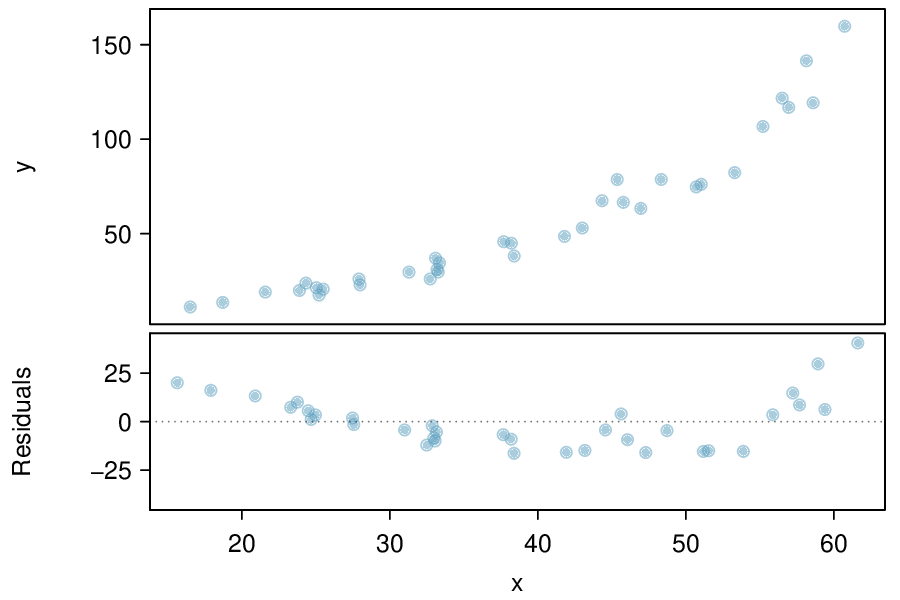
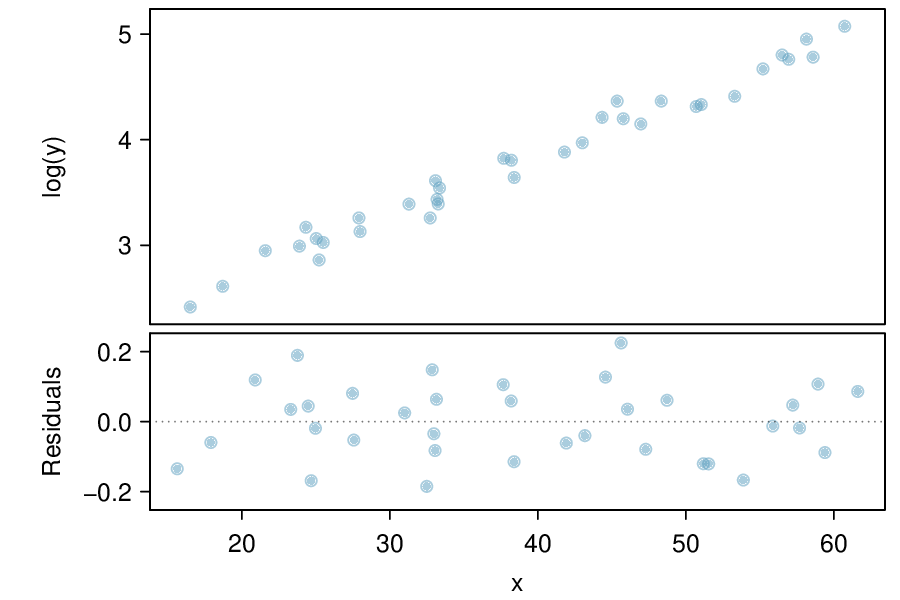
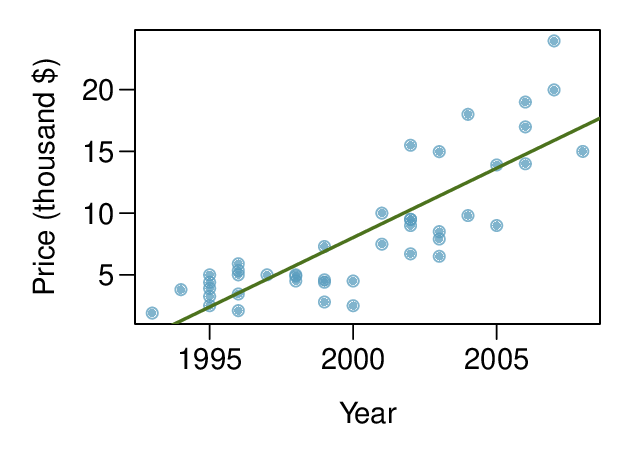
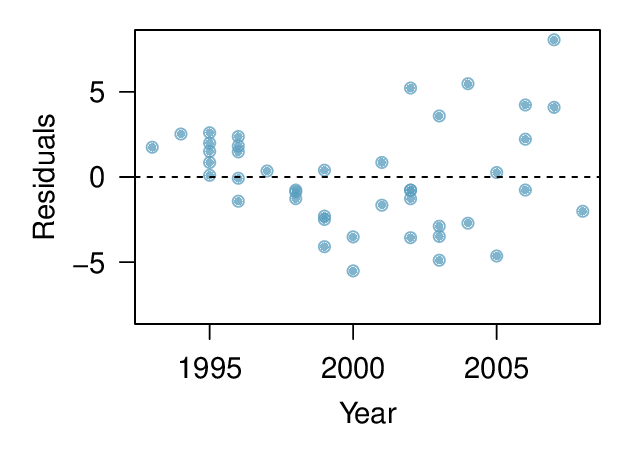
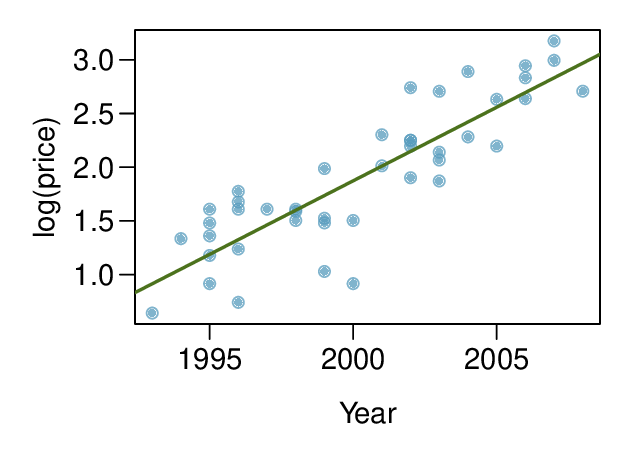
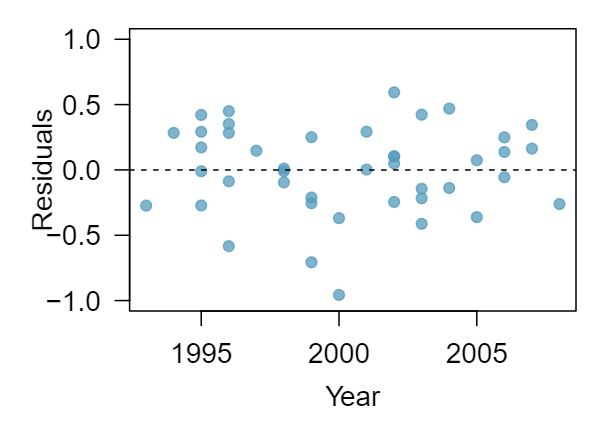
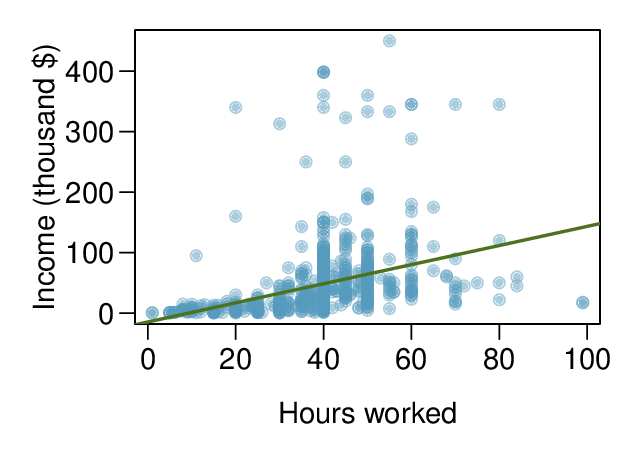
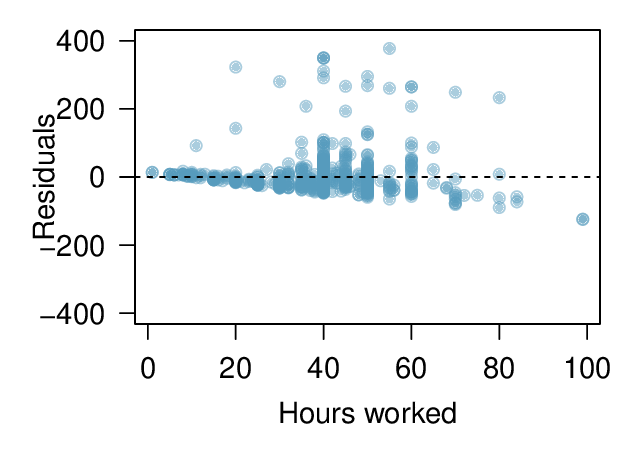
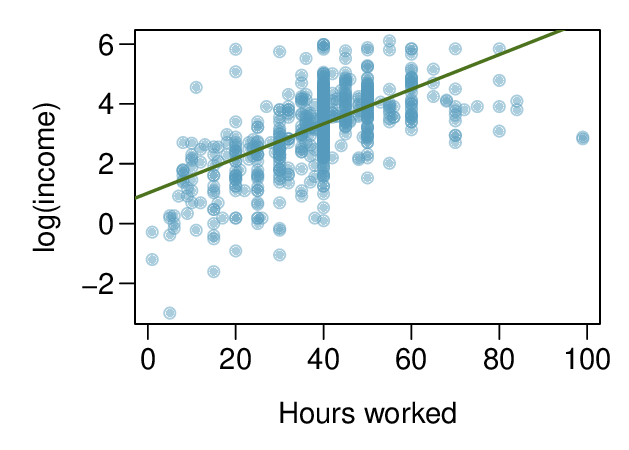
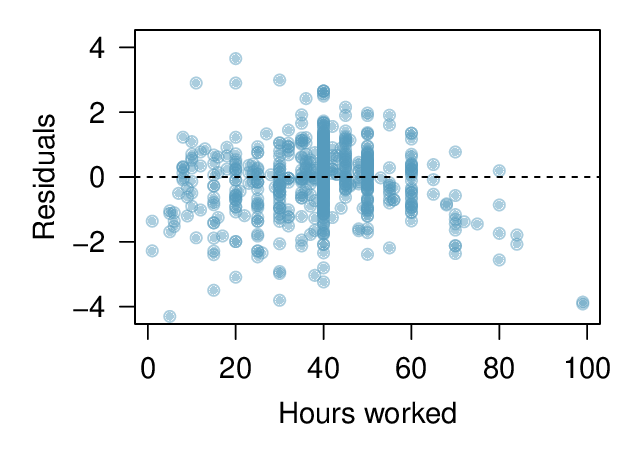
We can note the \(R^2\) value is fairly large. However, this alone does not mean that the model is good. Another model might be much better. When assessing the appropriateness of a linear model, we should look at the residual plot. The \(\cup\)-pattern in the residual plot tells us the original data is curved. If we inspect the two plots, we can see that for small and large values of \(x\) we systematically underestimate \(y\text{,}\) whereas for middle values of \(x\text{,}\) we systematically overestimate \(y\text{.}\) The curved trend can also be seen in the original scatterplot. Because of this, the linear model is not appropriate, and it would not be appropriate to perform a \(t\)-test for the slope because the conditions for inference are not met. However, we might be able to use a transformation to linearize the data.