Skip to main content

Advanced High School Statistics: Third Edition

David M Diez, Mine Çetinkaya-Rundel, Leah Dorazio, Christopher D Barr

Section 3.6 Binomial Distribution

What is the probability of exactly 50 heads in 100 coin tosses? Or the probability of randomly sampling 12 people and having more than 9 of them identify as male? If the probability of a defective part is 1%, how many defective items would we expect in a random shipment of 200 of those parts? We can model these scenarios and answer these questions using the binomial distribution.

Subsection 3.6.1 Introducing the binomial formula

Let’s again imagine ourselves back at the insurance agency where 70% of individuals do not exceed their deductible. Each people can be thought of as a trial. We label a trial a success if the individual healthcare costs do not exceed the deductible. We label a trial a failure if the individual healthcare costs do exceed her deductible. Because 70% of the individuals will not hit their deductible, we denote the probability of a success as \(p = 0.7\text{.}\)

Example 3.6.1.

Suppose the insurance agency is considering a random sample of four individuals they insure. What is the chance exactly one of them will exceed the deductible and the other three will not? Let’s call the four people Ariana (\(A\)), Brittany (\(B\)), Carlton (\(C\)), and Damian (\(D\)) for convenience.
Solution.
Let’s consider a scenario where one person exceeds the deductible:
\begin{align*} \amp P(A=\text{exceed, } B= \text{not, } C=\text{not, } D= \text{not} )\\ \amp = P(A=\text{exceed} )\ P(B=\text{not} )\ P(C=\text{not} )\ P(D=\text{not} )\\ \amp = (0.3)(0.7)(0.7) (0.7)\\ \amp = (0.7)^3 (0.3)^1\\ \amp = 0.103 \end{align*}
But there are three other scenarios: Brittany, Carlton, or Damian could have been the one to exceed the deductible. In each of these cases, the probability is again \((0.7)^3 (0.3)^1\text{.}\) These four scenarios exhaust all the possible ways that exactly one of these four people could have exceeded the deductible, so the total probability is \(4 \times (0.7)^3 (0.3)^1 =0.412\text{.}\)

Guided Practice 3.6.2.

Verify that the scenario where Brittany is the only one to exceed the deductible has probability \((0.7)^3 (0.3)^1\text{.}\)
 1 
\(P(A= \text{not, } B= \text{exceed, } C=\text{not, } D=\text{not}) =(0.7)(0.3)(0.7)(0.7)=(0.7)^3(0.3)^1\)
The binomial distribution describes the probability of having exactly \(x\) successes in \(n\) independent trials with probability of a success \(p\) (in Example 3.6.1.1, \(n=4\text{,}\) \(x=3\text{,}\) \(p=0.7\)). We would like to determine the probabilities associated with the binomial distribution more generally, i.e. we want a formula where we can use \(n\text{,}\) \(x\text{,}\) and \(p\) to obtain the probability. To do this, we reexamine each part of Example 3.6.1.1.
There were four individuals who could have been the one to exceed the deductible, and each of these four scenarios had the same probability. Thus, we could identify the final probability as
\begin{gather*} [ \text{number of scenarios}] \times P(\text{single scenario} ) \end{gather*}
The first component of this equation is the number of ways to arrange the \(x=3\) successes among the \(n=4\) trials. The second component is the probability of any of the four (equally probable) scenarios.
Consider \(P(\text{single scenario})\) under the general case of \(x\) successes and \(n-x\) failures in the \(n\) trials. In any such scenario, we apply the Multiplication Rule for independent events:
\begin{gather*} p^x (1 - p)^{n - x} \end{gather*}
This is our general formula for \(P(\text{single scenario})\text{.}\)
Secondly, we introduce the binomial coefficient, which gives the number of ways to choose \(x\) successes in \(n\) trials, i.e. arrange \(x\) successes and \(n - x\) failures:
\begin{gather*} {n \choose x} = \frac{n!}{x! (n - x)!} \end{gather*}
The quantity \({n \choose x}\) is read n choose x.
 2 
Other notations for \(n\) choose \(x\) includes \(_nC_x\text{,}\) \(C_n^x\text{,}\) and \(C(n,x)\text{.}\)
The exclamation point notation (e.g. \(n!\)) denotes a factorial expression.
\begin{align*} \amp 0! = 1\\ \amp 1! = 1\\ \amp 2! = 2\times1 = 2\\ \amp 3! = 3\times2\times1 = 6\\ \amp 4! = 4\times3\times2\times1 = 24\\ \amp \vdots\\ \amp n! = n\times(n-1)\times...\times3\times2\times1 \end{align*}
Using the formula, we can compute the number of ways to choose \(x = 3\) successes in \(n = 4\) trials:
\begin{gather*} {4 \choose 3} = \frac{4!}{3!(4-3)!} = \frac{4!}{3!1!} = \frac{4\times3\times2\times1}{(3\times2\times1) (1)} = 4 \end{gather*}
This result is exactly what we found by carefully thinking of each possible scenario in Example 3.6.1.1.
Substituting \(n\) choose \(x\) for the number of scenarios and \(p^x(1-p)^{n-x}\) for the single scenario probability yields the binomial formula.

Binomial formula.

Suppose the probability of a single trial being a success is \(p\text{.}\) Then the probability of observing exactly \(x\) successes in \(n\) independent trials is given by
\begin{gather*} P(X=x)={n\choose x}p^x(1-p)^{n-x} = \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \end{gather*}

Subsection 3.6.2 When and how to apply the formula

Is it binomial? Four conditions to check..

  1. The trials are independent.
  2. The number of trials, \(n\text{,}\) is fixed.
  3. Each trial outcome can be classified as a success or failure.
  4. The probability of a success, \(p\text{,}\) is the same for each trial.

Example 3.6.3.

What is the probability that 3 of 8 randomly selected individuals will have exceeded the insurance deductible, i.e. that 5 of 8 will not exceed the deductible? Recall that 70% of individuals will not exceed the deductible.
Solution.
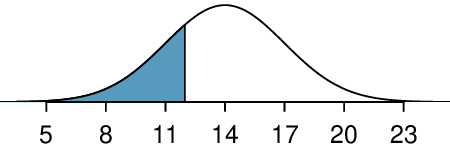
We would like to apply the binomial model, so we check the conditions. The number of trials is fixed (\(n = 8\)) (condition 2) and each trial outcome can be classified as a success or failure (condition 3). Because the sample is random, the trials are independent (condition 1) and the probability of a success is the same for each trial (condition 4).
In the outcome of interest, there are \(x = 5\) successes in \(n = 8\) trials (recall that a success is an individual who does not exceed the deductible, and the probability of a success is \(p = 0.7\text{.}\) So the probability that 5 of 8 will not exceed the deductible and 3 will exceed the deductible is given by
\begin{align*} { 8 \choose 5}(0.7)^5 (1-0.7)^{8-5} \amp = \frac{8!}{5!(5-3)!} (0.7)^5(1-0.7)^{8-5}\\ \amp = \frac{8!}{5!3!} (0.7)^5(0.3)^3 \end{align*}
Dealing with the factorial part:
\begin{gather*} \frac{8!}{5!3!} = \frac{8\times7\times6\times5\times4\times3\times2\times1} {(5\times4\times3\times2\times1)(3\times2\times1)} = \frac{8\times7\times6}{3\times2\times1} = 56 \end{gather*}
Using \((0.7)^5(0.3)^3 \approx 0.00454\text{,}\) the final probability is about \(56\times 0.00454 \approx 0.254\text{.}\)
If you must calculate the binomial coefficient by hand, it’s often useful to cancel out as many terms as possible in the top and bottom. See Section 3.6.3 for how to evaluate the binomial coefficient and the binomial formula using a calculator.

Computing binomial probabilities.

The first step in using the binomial model is to check that the model is appropriate. The second step is to identify \(n\text{,}\) \(p\text{,}\) and \(x\text{.}\) Finally, apply the binomial formula to determine the probability and interpret the results.

Example 3.6.4.

Approximately 35% of a population has blood type O+. Suppose four people show up at a hospital and we want to find the probability that exactly one of them has blood type O+. Can we use the binomial formula?
Solution.
To check if the binomial model is appropriate, we must verify the conditions.
  1. We will suppose that these 4 people comprise a random sample, then we can treat them as independent. This seems reasonable, since one person with a particular blood type showing up at a hospital seems unlikely to affect the chance that other people with that blood type would show up at the hospital.
  2. We have a fixed number of trials (\(n=4\)).
  3. Each outcome is a success or failure (blood type O+ or not blood type O+).
  4. The probability of a success is the same for each trial since the individuals are like a random sample (\(p=0.35\) if we say a “success” is someone having blood type O+).

Sampling Without Replacement.

When randomly sampling without replacement, if the sample size is small relative to the population size (rule of thumb: sample size less than 1/10 of the population size), we will consider the observations to be independent.

Example 3.6.5.

Given that 35% of a population has blood type O+, what is the probabilty that in a random sample of 4 people:
  1. none of them have blood type O+?
  2. one will have blood type O+?
  3. no more than one will have blood type O+?
Solution.
Compute parts (a) and (b) using the binomial formula:
  1. \(P(X=0) = {4 \choose 0} (0.35)^0 (0.65)^4 = 1\times1\times 0.65^4 = 0.65^4 = 0.179\) Note that we could have answered this question without the binomial formula, using methods from the previous section.
  2. \(P(X=1) = {4 \choose 1} (0.35)^1(0.65)^{3} = 0.384\text{.}\)
  3. This can be computed as the sum of parts (a) and (b): \(P(X=0) + P(X=1) = 0.179 + 0.384 = 0.563\text{.}\) That is, there is about a 56.3% chance that no more than one of them will have blood type O+.

Guided Practice 3.6.6.

What is the probability that at least 3 of 4 people in a random sample will have blood type O+ if 35% of the population has blood type O+?
 3 
\(P(\text{at least 3 of 4 have blood type O+})=P(X=3)+P(X=4)={ 4 \choose 3}(0.35)^3(0.65)^1+(0.35)^4=0.111+0.015=0.126\)

Guided Practice 3.6.7.

The probability that a random smoker will develop a severe lung condition in his or her lifetime is about \(0.3\text{.}\) If you have 4 friends who smoke and you want to find the probability that 1 of them will develop a severe lung condition in his or her lifetime, can you apply the binomial formula?
 4 
While conditions (2) and (3) are met, most likely the friends know each other, so the independence assumption (1) is probably not satisfied. For example, acquaintances may have similar smoking habits, or those friends might make a pact to quit together. Condition (4) is also not satisfied since this is not a random sample of people.

Example 3.6.8.

There are 13 marbles in a bag. 4 are blue and 9 are red. Randomly draw 5 marbles without replacement. Find the probability you get exactly 3 blue marbles.
Solution.
Because the probability of success \(p\) is not the same for each trial, we cannot use the binomial formula. However, we can use the same logic to arrive at the following answer.
\begin{align*} P(X = 3) \amp = (\text{number of combinations with 3 blue } )\times P(\text{3 blue and 2 red in a specific order})\\ \amp ={5\choose 3}\times P(\text{ BBBRR } )\\ \amp = {5\choose 3}\left(\frac{4}{13}\times \frac{3}{12}\times \frac{2}{11} \times \frac{9}{10} \times \frac{8}{9}\right)\\ \amp = 0.1119 \end{align*}

Guided Practice 3.6.9.

Draw 4 cards without replacement from a deck of 52 cards. What is the probability that you get at least two hearts?
 5 
\(P(\text{at least 2 hearts in 4 draws from a deck})=1-[P(X=0)+P(X=1)]=1-[(\frac{39}{52}) (\frac{38}{51}) (\frac{37}{50}) (\frac{36}{49})+{4\choose 1}(\frac{13}{52}) (\frac{39}{51}) (\frac{38}{50}) (\frac{37}{49})]=1-[0.03038+0.4388]=0.2574\)
Lastly, we consider the binomial coefficient,, \(n\) choose \(x\text{,}\) under some special scenarios.

Guided Practice 3.6.10.

Why is it true that \({n \choose 0}=1\) and \({n \choose n}=1\) for any number \(n\text{?}\)
 6 
Frame these expressions into words. How many different ways are there to arrange 0 successes and \(n\) failures in \(n\) trials? (1 way.) How many different ways are there to arrange \(n\) successes and 0 failures in \(n\) trials? (1 way.)

Guided Practice 3.6.11.

How many ways can you arrange one success and \(n-1\) failures in \(n\) trials? How many ways can you arrange \(n-1\) successes and one failure in \(n\) trials?
 7 
One success and \(n-1\) failures: there are exactly n unique places we can put the success, so there are \(n\) ways to arrange one success and \(n-1\) failures. A similar argument is used for the second question. Mathematically, we show these results by verifying the following two equations:\({n \choose 1}=n\text{,}\) \({n \choose {n-1}}=n\)

Subsection 3.6.3 Technology: binomial probabilities

Get started quickly with this Desmos Binomial Calculator
 8 
www.desmos.com/calculator/xwe9ywwjik
(available at openintro.org/ahss/desmos
 9 
openintro.org/ahss/desmos
).
Calculator instructions

TI-83/84: Computing the binomial coefficient \({n\choose x}\).

Use MATH, PRB, nCr to evaluate \(n\) choose \(r\text{.}\) Here \(r\) and \(x\) are different letters for the same quantity.
  1. Type the value of \(n\text{.}\)
  2. Select MATH.
  3. Right arrow to PRB.
  4. Choose 3:nCr.
  5. Type the value of \(x\text{.}\)
  6. Hit ENTER.
Example: 5 nCr 3 means 5 choose 3.

Casio fx-9750GII: Computing the binomial coefficient \({n\choose x}\).

  1. Navigate to the RUN-MAT section (hit MENU, then hit 1).
  2. Enter a value for \(n\text{.}\)
  3. Go to CATALOG (hit buttons SHIFT and then 7).
  4. Type C (hit the ln button), then navigate down to the bolded C and hit EXE.
  5. Enter the value of \(x\text{.}\) Example of what it should look like: 7C3.
  6. Hit EXE.

TI-84: Computing the binomial formula, \(P(X = {x)={n\choose x}p^x(1-p)^{n-x}}\).

Use 2ND VARS, binompdf to evaluate the probability of exactly \(x\) occurrences out of \(n\) independent trials of an event with probability \(p\text{.}\)
  1. Select 2ND VARS (i.e. DISTR)
  2. Choose A:binompdf (use the down arrow to scroll down).
  3. Let trials be \(n\text{.}\)
  4. Let p be \(p\)
  5. Let x value be \(x\text{.}\)
  6. Select Paste and hit ENTER.
TI-83: Do step 1, choose 0:binompdf, then enter \(n\text{,}\) \(p\text{,}\) and \(x\) separated by commas:
binompdf(n, p, x). Then hit ENTER.

TI-84: Computing \(P(X \le {x)= {n\choose 0}p^0(1-p)^{n-0} + ... + {n\choose x}p^x(1-p)^{n-x}}\).

Use 2ND VARS, binomcdf to evaluate the cumulative probability of at most \(x\) occurrences out of \(n\) independent trials of an event with probability \(p\text{.}\)
  1. Select 2ND VARS (i.e. DISTR)
  2. Choose B:binomcdf (use the down arrow).
  3. Let trials be \(n\text{.}\)
  4. Let p be \(p\)
  5. Let x value be \(x\text{.}\)
  6. Select Paste and hit ENTER.
TI-83: Do steps 1-2, then enter the values for \(n\text{,}\) \(p\text{,}\) and \(x\) separated by commas as follows: binomcdf(n, p, x). Then hit ENTER.

Casio fx-9750GII: Binomial calculations.

  1. Navigate to STAT (MENU, then hit 2).
  2. Select DIST (F5), and then BINM (F5).
  3. Choose whether to calculate the binomial distribution for a specific number of successes, \(P(X = k)\text{,}\) or for a range \(P(X \leq k)\) of values (0 successes, 1 success, ..., \(x\) successes).
    • For a specific number of successes, choose Bpd (F1).
    • To consider the range 0, 1, ..., \(x\) successes, choose Bcd(F1).
  4. If needed, set Data to Variable (Var option, which is F2).
  5. Enter the value for x (\(x\)), Numtrial (\(n\)), and p (probability of a success).
  6. Hit EXE.

Guided Practice 3.6.12.

Find the number of ways of arranging 3 blue marbles and 2 red marbles.
 10 
Here c\(=5\) and x\(=3\text{.}\) Doing 5 nCr 3 gives the number of combinations as 10

Guided Practice 3.6.13.

There are 13 marbles in a bag. 4 are blue and 9 are red. Randomly draw 5 marbles with replacement. Find the probability you get exactly 3 blue marbles.
 11 
Here, \(n=5\text{,}\) \(p=4/13\) and \(x=3\text{,}\) so set trials\(=5\text{,}\) p\(=4/13\) and x value\(=3\text{.}\) The probability is 0.1396.

Guided Practice 3.6.14.

There are 13 marbles in a bag. 4 are blue and 9 are red. Randomly draw 5 marbles with replacement. Find the probability you get at most 3 blue marbles (i.e. less than or equal to 3 blue marbles).
 12 
Similarly, set trials\(=5\text{,}\) p\(=4/13\) and x value\(=3\text{.}\) The cumulative probability is 0.9662

Subsection 3.6.4 An example of a binomial distribution

In Example 3.6.5, we asked various probability questions regarding the number of people out of 4 with blood type O+. We verified that the scenario was binomial and that each problem could be solved using the binomial formula. Instead of looking at it piecewise, we could describe the entire distribution of possible values and their corresponding probabilities. Since there are 4 people, there are several possible outcomes for the number who might have blood type O+: 0, 1, 2, 3, 4. We can make a distribution table with these outcomes. Recall that the probability of a randomly sampled person being blood type O+ is about 0.35.
The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which described the number of trials we must wait before we observe a success.
\(x_i\) \(P(x_i)\)
0 \({4\choose 0}(0.35)^0(0.65)^{4} = 0.179\)
1 \({4\choose 1}(0.35)^1(0.65)^{3} = 0.384\)
2 \({4\choose 2}(0.35)^2(0.65)^{2} = 0.311\)
3 \({4\choose 3}(0.35)^3(0.65)^{1} = 0.111\)
4 \({4\choose 4}(0.35)^4(0.65)^{0} = 0.015\)
Figure 3.6.15. Probability distribution for the number with blood type O+ in a random sample of 4 people. This is a binomial distribution. Correcting for rounding error, the probabilities add up to 1, as they must for any probability distribution.

Subsection 3.6.5 The mean and standard deviation of a binomial distribution

Since this is a probability distribution we could find its mean and standard deviation using the formulas from Chapter 3. Those formulas require a lot of calculations, so it is fortunate there’s an easier way to compute the mean and standard deviation for a binomial random variable.

Mean and standard deviation of the binomial distribution.

For a binomial distribution with parameters \(n\) and \(p\text{,}\) where \(n\) is the number of trials and \(p\) is the probability of a success, the mean and standard deviation of the number of observed successes are
\begin{align*} \mu_{x} \amp = np \amp \sigma_{x} \amp = \sqrt{np(1-p)} \end{align*}

Example 3.6.16.

If the probability that a person has blood type O+ is 0.35 and you have 40 randomly selected people, about how many would you expect to have blood type O+? What is the standard deviation of the number of people who would have blood type O+ among the 40 people?
Solution.
We are asked to determine the expected number (the mean) and the standard deviation, both of which can be directly computed from the formulas above.
\begin{align*} \mu_{X}\amp =np = 40(0.35) = 14\\ \sigma_{X} \amp = \sqrt{np(1-p)} = \sqrt{40(0.35)(0.65)} = 3.0 \end{align*}
The exact distribution is shown in Figure 3.6.17.
Figure 3.6.17. Distribution for the number of people with blood type O+ in a random sample of size 40, where \(p=0.35\text{.}\) The distribution is binomial and is centered on 14 with a standard deviation of 3.

Subsection 3.6.6 Normal approximation to the binomial distribution

The binomial formula is cumbersome when the sample size (\(n\)) is large, particularly when we consider a range of observations.

Example 3.6.18.

Find the probability that fewer than 12 out of 40 randomly selected people would have blood type O+, where probability of blood type O+ is 0.35.
Solution.
This is equivalent to asking, what is the probability of observing \(X=0, 1, 2, ..., \text{ or } 11\) with blood type O+ in a sample of size 40 when \(p=0.35\text{?}\) We previously verified that this scenario is binomial. We can compute each of the 12 probabilities using the binomial formula and add them together to find the answer:
\begin{align*} \amp P(X=0\text{ or } X=1\text{ or } \cdots\text{ or } X=11)\\ \amp \qquad = P(X=0) + P(X=1) + \cdots + P(X=11)\\ \amp \qquad = {40\choose 0}(0.35)^0(0.65)^{40} + {40\choose 1}(0.35)^1(0.65)^{39} + \cdots + {40\choose 11}(0.35)^{11}(0.65)^{29}\\ \amp \qquad = 0.21 \end{align*}
If the true proportion with blood type O+ in the population is \(p = 0.35\text{,}\) then the probability of observing fewer than 12 in a sample of \(n = 40\) is 0.21.
The computations in Example 3.6.18 are tedious and long. In general, we should avoid such work if an alternative method exists that is faster, easier, and still accurate. Recall that calculating probabilities of a range of values is much easier in the normal model. In some cases we may use the normal distribution to estimate binomial probabilities. While a normal approximation for the distribution in Figure 3.6.15 when the sample size was \(n = 4\) would not be appropriate, it might not be too bad for the distribution in Figure 3.6.17 where \(n = 40\text{.}\) We might wonder, when is it reasonable to use the normal model to approximate a binomial distribution?

Guided Practice 3.6.19.

Here we consider the binomial model when the probability of a success is \(p=0.10\text{.}\) Figure 3.6.20 shows four hollow histograms for simulated samples from the binomial distribution using four different sample sizes: \(n=10, 30, 100, 300\text{.}\) What happens to the shape of the distributions as the sample size increases? How does the binomial distribution change as \(n\) gets larger?
 13 
The distribution is transformed from a blocky and skewed distribution into one that rather resembles the normal distribution in the last hollow histogram.
Figure 3.6.20. Hollow histograms of samples from the binomial model when \(p=0.10\text{.}\) The sample sizes for the four plots are \(n=10\text{,}\) 30, 100, and 300, respectively.
The shape of the binomial distribution depends upon both \(n\) and \(p\text{.}\) Here we introduce a rule of thumb for when normal approximation of a binomial distribution is reasonable. We will use this rule of thumb in many applications going forward.

Normal approximation of the binomial distribution.

The binomial distribution with probability of success \(p\) is nearly normal when the sample size \(n\) is sufficiently large that \(np\ge 10\) and \(n(1-p)\ge 10\text{.}\) The approximate normal distribution has parameters corresponding to the mean and standard deviation of the binomial distribution:
\begin{align*} \mu \amp = np \amp \amp \sigma= \sqrt{np(1-p)} \end{align*}
The normal approximation may be used when computing the range of many possible successes. For instance, we may apply the normal distribution to the setting described in Figure 3.6.17.

Example 3.6.21.

Use the normal approximation to estimate the probability of observing fewer than 12 with blood type O+ in a random sample of 40, if the true proportion with blood type O+ in the population is \(p=0.35\text{.}\)
Solution.
First we verify that \(np\) and \(n(1-p)\) are at least 10 so that we can apply the normal approximation to the binomial model:
\begin{align*} np\amp = 40(0.35)=14\ge 10 \amp n(1-p)\amp = 40(0.65) = 26\ge 10 \end{align*}
With these conditions checked, we may use the normal distribution to approximate the binomial distribution with the following mean and standard deviation:
\begin{align*} \mu \amp = np = 40(0.35)=14\\ \sigma \amp = \sqrt{np(1-p)} = \sqrt{40(0.35)(0.65)} = 3.0 \end{align*}
We want to find the probability of observing fewer than 12 with blood type O+ using this model. We note that 12 is less than 1 standard deviation below the mean:
Next, we compute the Z-score as \(Z=\frac{12 - 14}{3} = -0.67\) to find the shaded area in the picture: \(P(Z \lt -0.67) = 0.25\text{.}\) This probability of 0.25 using the normal approximation is reasonably close to the true probability of 0.21 computed using the binomial distribution.

Example 3.6.22.

Use the normal approximation to estimate the probability of observing fewer than 120 people with blood type O+ in a random sample of 400, if the true proportion with blood type O+ in the population is \(p=0.35\text{.}\)
Solution.
We have previously verified that the binomial model is reasonable for this context. Now we will verify that both \(np\) and \(n(1-p)\) are at least 10 so we can apply the normal approximation to the binomial model:
\begin{align*} np\amp =400(0.35)=140\ge 10 \amp n(1-p)\amp =400(0.65)=260\ge 10 \end{align*}
With these conditions checked, we may use the normal approximation in place of the binomial distribution with the following mean and standard deviation:
\begin{align*} \mu \amp = np = 400(0.35)=140\\ \sigma \amp = \sqrt{np(1-p)} = \sqrt{400(0.35)(0.65)}= 9.5 \end{align*}
We want to find the probability of observing fewer than 120 with blood type O+ using this model. We note that 120 is just over 2 standard deviations below the mean:
Next, we compute the Z-score as \(Z=\frac{120 - 140}{9.5} = -2.1\) to find the shaded area in the picture: \(P(Z \lt -2.1) = 0.0179\text{.}\) This probability of 0.0179 using the normal approximation is very close to the true probability of 0.0196 from the binomial distribution.

Guided Practice 3.6.23.

Use normal approximation, if applicable, to estimate the probability of getting greater than 15 sixes in 100 rolls of a fair die.
 14 
\(np=100(1/6)=16.7 \ge 10\) and \(n(1-p)=100(5/6)=83.3 \ge 10\) and \(\mu=np=100(1/6) = 16.7 \text{ ; } \sigma = \sqrt{np(1-p)}= \sqrt{100(1/6)(5/6)}=3.7\) and \(Z=\frac{15-16.7}{3.7}=-0.46 \text{ ; } P(Z>-0.46)=0.677\)

Subsection 3.6.7 Normal approximation breaks down on small intervals (special topic)

The normal approximation may fail on small intervals.

The normal approximation to the binomial distribution tends to perform poorly when estimating the probability of a small range of counts, even when the conditions are met.
We consider again our example where 35% of people are blood type O+. Suppose we want to find the probability that between 129 and 131 people, inclusive, have blood type O+ in a random sample of 400 people. We want to compute the probability of observing 129, 130, or 131 people with blood type O+ when \(p=0.20\) and \(n=400\text{.}\) With such a large sample, we might be tempted to apply the normal approximation and use the range 129 to 131. However, we would find that the binomial solution and the normal approximation notably differ:
\begin{align*} \text{ Binomial: } \amp \ 0.0732 \amp \text{ Normal: } \amp \ 0.0483 \end{align*}
We can identify the cause of this discrepancy using Figure 3.6.24, which shows the areas representing the binomial probability (outlined) and normal approximation (shaded). Notice that the width of the area under the normal distribution is 0.5 units too slim on both sides of the interval. The binomial distribution is a discrete distribution, and the each bar is centered over an integer value. Looking closely at Figure 3.6.24, we can see that the bar corresponding to 129 begins at 128.5 and ends at 129.5, the bar corresponding to 131 begins at 130.5 and ends at 131.5, etc.
Figure 3.6.24. A normal curve with the area between 129 and 131 shaded. The outlined area from 128.5 to 131.5 represents the exact binomial probability.

Improving accuracy of the normal approximation to the binomial distribution.

The normal approximation to the binomial distribution for intervals of values is usually improved if cutoff values for the lower end of a shaded region are reduced by 0.5 and the cutoff value for the upper end are increased by 0.5. This correction is called the continuity correction and accounts for the fact that the binomial distribution is discrete.

Example 3.6.25.

Use the method described to find a more accurate estimate for the probability of observing 129, 130, or 131 people with blood type O+ in 400 randomly selected people when \(p=0.35\text{.}\)
Solution.
Instead of standardizing 129 and 131, we will standardize 128.5 and 131.5:
\begin{align*} Z_{left} \amp = \frac{128.5-140}{9.5} = -1.263\\ Z_{right} \amp = \frac{131.5-140}{9.5} = -0.895\\ P(-1.263 \amp \lt Z \lt -0.895) = 0.0772 \end{align*}
The probability 0.0772 is much closer to the true value of 0.0732 than the previous estimate of 0.0483 we calculated using normal approximation without the continuity correction.
It is always possible to apply the continuity correction when finding a normal approximation to the binomial distribution. However, when \(n\) is very large or when the interval is wide, the benefit of the modification is limited since the added area becomes negligible compared to the overall area being calculated.

Subsection 3.6.8 Section summary

  • \(n\choose x\text{,}\) the binomial coefficient, describes the number of combinations for arranging \(x\) successes among \(n\) trials. \(n\choose x\) \(=\frac{n!}{x!(n-x)!}\text{,}\) where \(n!=1\times 2\times 3\times...n\text{,}\) and \(0!=0\text{.}\)
  • The binomial formula can be used to find the probability that something happens exactly x times in n trials. Suppose the probability of a single trial being a success is \(p\text{.}\) Then the probability of observing exactly \(x\) successes in \(n\) independent trials is given by
    \begin{gather*} {n\choose x}p^x(1-p)^{n-x} = \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \end{gather*}
  • To apply the binomial formula, the events must be independent from trial to trial. Additionally, \(n\text{,}\) the number of trials must be fixed in advance, and \(p\text{,}\) the probability of the event occurring in a given trial, must be the same for each trial.
  • To use the binomial formula, first confirm that the binomial conditions are met. Next, identify the number of trials \(n\text{,}\) the number of times the event is to be a “success” \(x\text{,}\) and the probability that a single trial is a success \(p\text{.}\) Finally, plug these three numbers into the formula to get the probability of exactly \(x\) successes in \(n\) trials.
  • To find a probability involving at least or at most, first determine if the scenario is binomial. If so, apply the binomial formula as many times as needed and add up the results. e.g.
    \begin{gather*} P(\text{ at least 3 Heads in 5 tosses of a fair coin } )\\ =P(\text{ exactly 3 Heads } )+P(\text{ exactly 4 Heads } )+P(\text{ exactly 5 Heads } ) \end{gather*}
    where each probability can be found using the binomial formula.
  • The distribution of the number of successes in \(n\) independent trials gives rise to a binomial distribution. If X has a binomial distribution with parameters \(n\) and \(p\text{,}\) then \(P(X=x) = {n\choose x}p^x(1-p)^n-x\text{,}\) where \(x=0,1,2,3\dots,n\text{.}\)
  • To write out a binomial probability distribution table, list all possible values for \(x\text{,}\) the number of successes, then use the binomial formula to find the probability of each of those values.
  • If X follows a binomial distribution with parameters \(n\) and \(p\text{,}\) then:
    • The mean is given by \(\mu_{\scriptscriptstyle{X}} = np\text{.}\) (center)
    • The standard deviation is given by \(\sigma_{\scriptscriptstyle{X}} = \sqrt{np(1-p)}\text{.}\) (spread)
    • When \(np\ge 10\) and \(n(1-p)\ge 10\text{,}\) the binomial distribution is approximately normal. (shape)

Exercises 3.6.9 Exercises

1. Exploring combinations.

A coin is tossed 5 times. How many sequences / combinations of Heads/Tails are there that have:
  1. Exactly 1 Tail?
  2. Exactly 4 Tails?
  3. Eactly 3 Tails?
  4. At least 3 Tails?
Solution.
  1. \({5 \choose 1}=5\text{.}\)
  2. \({5 \choose 4}=5\text{.}\)
  3. \({5 \choose 3}=10\text{.}\)
  4. \({5 \choose 3} +{5 \choose 4}+ {5 \choose 5}=10+5+1 =16\text{.}\)

2. Political affiliation.

Suppose that in a large population, 51% identify as Democrat. A researcher takes a random sample of 3 people.
  1. Use the binomial model to calculate the probability that two of them identify as Democrat.
  2. Write out all possible orderings of 3 people, 2 of whom identify as Democrat. Use these scenarios to calculate the same probability from part (a) but using the Addition Rule for disjoint events. Confirm that your answers from parts (a) and (b) match.
  3. If we wanted to calculate the probability that a random sample of 8 people will have 3 that identify as Democrat, briefly describe why the approach from part (b) would be more tedious than the approach from part (a).

3. Underage drinking, Part I.

Data collected by the Substance Abuse and Mental Health Services Administration (SAMSHA) suggests that 69.7% of 18-20 year olds consumed alcoholic beverages in any given year.
 15 
SAMHSA, Office of Applied Studies, National Survey on Drug Use and Health, 2007 and 2008.
  1. Suppose a random sample of ten 18-20 year olds is taken. Is the use of the binomial distribution appropriate for calculating the probability that exactly six consumed alcoholic beverages? Explain.
  2. Calculate the probability that exactly 6 out of 10 randomly sampled 18- 20 year olds consumed an alcoholic drink.
  3. What is the probability that exactly four out of ten 18-20 year olds have not consumed an alcoholic beverage?
  4. What is the probability that at most 2 out of 5 randomly sampled 18-20 year olds have consumed alcoholic beverages?
  5. What is the probability that at least 1 out of 5 randomly sampled 18-20 year olds have consumed alcoholic beverages?
Solution.
  1. Binomial conditions are met: (1) Independent trials: In a random sample, whether or not one 18-20 year old has consumed alcohol does not depend on whether or not another one has. (2) Fixed number of trials: \(n=10\text{.}\) (3) Only two outcomes at each trial: Consumed or did not consume alcohol. (4) Probability of a success is the same for each trial: \(p=0.697\text{.}\)
  2. 0.203.
  3. 0.203.
  4. 0.167.
  5. 0.997.

4. Chicken pox, Part I.

The National Vaccine Information Center estimates that 90% of Americans have had chickenpox by the time they reach adulthood.
 16 
National Vaccine Information Center, Chickenpox, The Disease & The Vaccine Fact Sheet
  1. Suppose we take a random sample of 100 American adults. Is the use of the binomial distribution appropriate for calculating the probability that exactly 97 out of 100 randomly sampled American adults had chickenpox during childhood? Explain.
  2. Calculate the probability that exactly 97 out of 100 randomly sampled American adults had chickenpox during childhood.
  3. What is the probability that exactly 3 out of a new sample of 100 American adults have not had chickenpox in their childhood?
  4. What is the probability that at least 1 out of 10 randomly sampled American adults have had chickenpox?
  5. What is the probability that at most 3 out of 10 randomly sampled American adults have not had chickenpox?

5. Game of dreidel.

A dreidel is a four-sided spinning top with the Hebrew letters nun, gimel, hei, and shin, one on each side. Each side is equally likely to come up in a single spin of the dreidel. Suppose you spin a dreidel three times. Calculate the probability of getting
  1. at least one nun?
  2. exactly 2 nuns?
  3. exactly 1 hei?
  4. at most 2 gimels?
Figure 3.6.26. Photo by Staccabees, cropped (http://flic.kr/p/7gLZTf)
 17 
www.flickr.com/photos/44689913@N04/4116667696/
, CC BY 2.0 license
 18 
creativecommons.org/licenses/by/2.0/
Solution.
  1. \(1-0.75^3=0.5781\text{.}\)
  2. 0.1406.
  3. 0.4219.
  4. \(1-0.25^3=0.9844\text{.}\)

6. Sickle cell anemia.

Sickle cell anemia is a genetic blood disorder where red blood cells lose their flexibility and assume an abnormal, rigid, “sickle” shape, which results in a risk of various complications. If both parents are carriers of the disease, then a child has a 25% chance of having the disease, 50% chance of being a carrier, and 25% chance of neither having the disease nor being a carrier. If two parents who are carriers of the disease have 3 children, what is the probability that
  1. two will have the disease?
  2. none will have the disease?
  3. at least one will neither have the disease nor be a carrier?
  4. the first child with the disease will the be \(3^{rd}\) child?

7. Underage drinking, Part II.

We learned in Exercise 3.6.9.3 that about 70% of 18-20 year olds consumed alcoholic beverages in any given year. We now consider a random sample of fifty 18-20 year olds.
  1. How many people would you expect to have consumed alcoholic beverages? And with what standard deviation?
  2. Would you be surprised if there were 45 or more people who have consumed alcoholic beverages?
  3. What is the probability that 45 or more people in this sample have consumed alcoholic beverages? How does this probability relate to your answer to part (b)?
Solution.
  1. \(\mu = 35\text{,}\) \(\sigma = 3.24\text{.}\)
  2. Yes. \(Z = \frac{45-35}{3.24}=3.09\text{.}\) 45 is more than 3 standard deviations from the mean, we can assume that it is an unusual observation. Therefore yes, we would be surprised.
  3. Using a normal model approximation, 0.0010. With a 0.5 correction, 0.0017.

8. Chickenpox, Part II.

We learned in Exercise 3.6.9.4 that about 90% of American adults had chickenpox before adulthood. We now consider a random sample of 120 American adults.
  1. How many people in this sample would you expect to have had chickenpox in their childhood? And with what standard deviation?
  2. Would you be surprised if there were 105 people who have had chickenpox in their childhood?
  3. What is the probability that 105 or fewer people in this sample have had chickenpox in their childhood? How does this probability relate to your answer to part (b)?

Subsection 3.6.10 Chapter Highlights

This chapter focused on understanding likelihood and chance variation, first by solving individual probability questions and then by investigating probability distributions.
The main probability techniques covered in this chapter are as follows:
  • The General Multiplication Rule for and probabilities (intersection), along with the special case when events are independent.
  • The General Addition Rule for or probabilities (union), along with the special case when events are mutually exclusive.
  • The Conditional Probability Rule.
  • Tree diagrams and Bayes’ Theorem to solve more complex conditional problems.
  • Simulations and the use of random digits to estimate probabilities.
Fundamental to all of these problems is understanding when events are independent and when they are mutually exclusive. Two events are independent when the outcome of one does not affect the outcome of the other, i.e. \(P(A | B) = P(A)\text{.}\) Two events are mutually exclusive when they cannot both happen together, i.e. \(P(A \text{ and } B) = 0\text{.}\)
Moving from solving individual probability questions to studying probability distributions helps us better understand chance processes and quantify expected chance variation.
  • For a discrete probability distribution, the sum of the probabilities must equal 1.
  • As with any distribution, one can calculate the mean and standard deviation of a probability distribution. In the context of a probability distribution, the mean and standard deviation describe the average and the typical deviation from the average, respectively, after many, many repetitions of the chance process.
  • A probability distribution can be summarized by its center (mean, median), spread (SD, IQR), and shape (right skewed, left skewed, approximately symmetric).
  • Adding a constant to every value in a probability distribution adds that value to the mean, but it does not affect the standard deviation. When multiplying every value by a constant, this multiplies the mean by the constant and it multiplies the standard deviation by the absolute value of the constant.
  • The mean of the sum of two random variables equals the sum of the means. However, this is not true for standard deviations. Instead, when finding the standard deviation of a sum or difference of random variables, take the square root of the sum of each of the standard deviations squared.
  • The geometric distribution provides a model for the number of trials until the first success, when the trials are independent.
  • The binomial distribution provides a model for the number of successes in n independent trials.
  • The geometric distribution is always right skewed. However, when the success-failure rule is met (at least 10 success and 10 failures), the binomial distribution can be modeled using a normal distribution with \(\text{mean} = np\) and standard deviation \(\sqrt{np(1-p)}\text{.}\)
The study of probability is useful for measuring uncertainty and assessing risk. In addition, probability serves as the foundation for inference, providing a framework for evaluating when an outcome falls outside of the range of what would be expected by chance alone.
You have attempted of activities on this page.
PrevTopNext