Skip to main content

Advanced High School Statistics: Third Edition

David M Diez, Mine Çetinkaya-Rundel, Leah Dorazio, Christopher D Barr

Section 2.6 Chapter exercises

Exercises Exercises

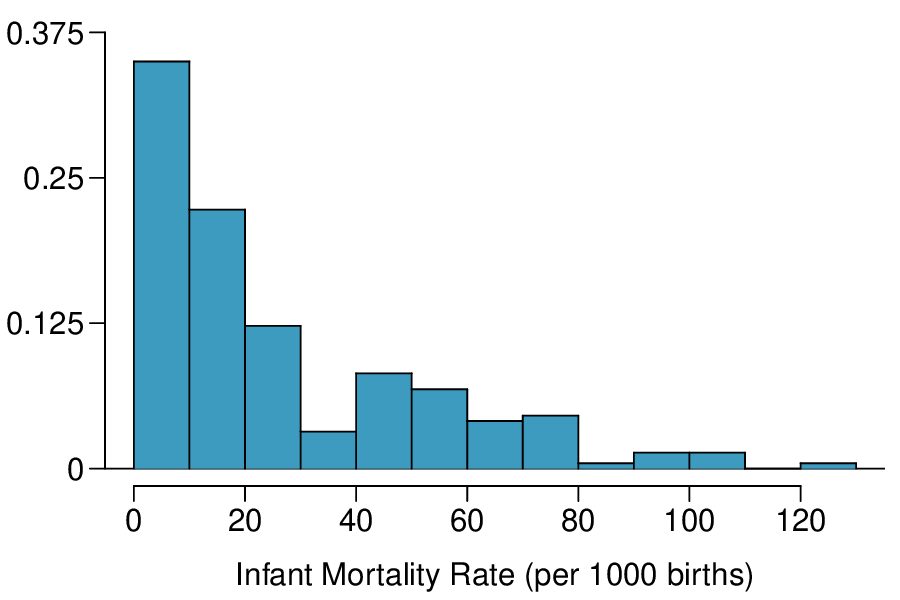
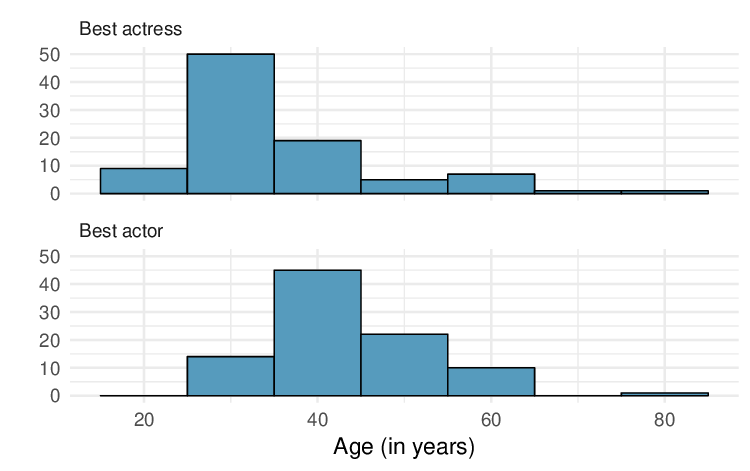
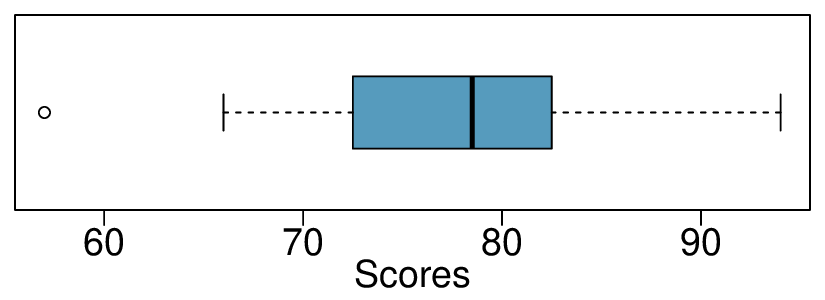
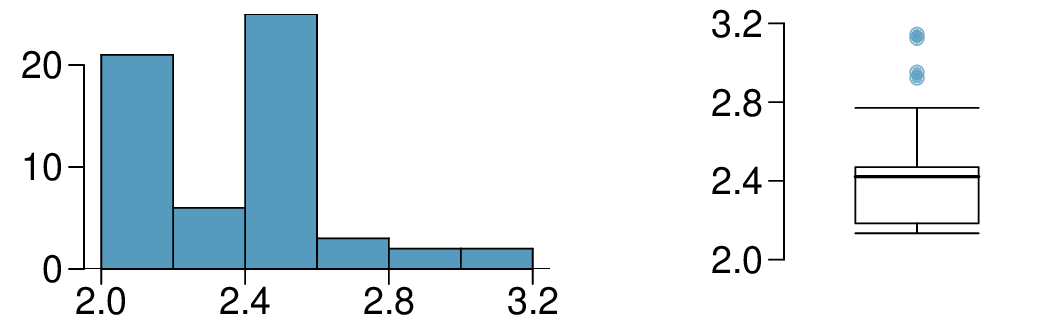
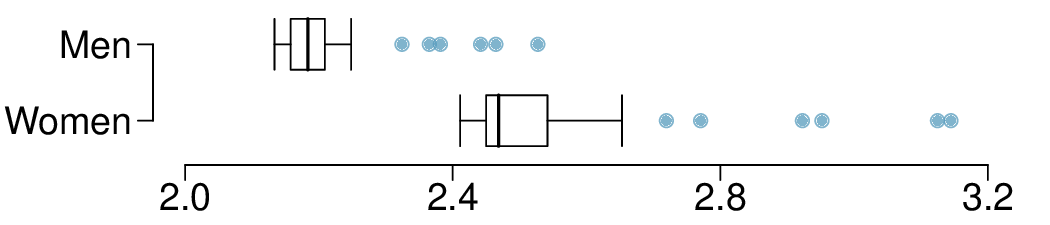
1. Make-up exam.

In a class of 25 students, 24 of them took an exam in class and 1 student took a make-up exam the following day. The professor graded the first batch of 24 exams and found an average score of 74 points with a standard deviation of 8.9 points. The student who took the make-up the following day scored 64 points on the exam.
  1. Does the new student’s score increase or decrease the average score?
  2. What is the new average?
  3. Does the new student’s score increase or decrease the standard deviation of the scores?
Solution.
  1. Decrease: the new score is smaller than the mean of the 24 previous scores.
  2. Calculate a weighted mean. Use a weight of 24 for the old mean and 1 for the new mean: \((24\times 74 + 1\times64)/(24+1) = 73.6\text{.}\)
  3. The new score is more than 1 standard deviation away from the previous mean, so increase.

2. Infant mortality.

The infant mortality rate is defined as the number of infant deaths per 1,000 live births. This rate is often used as an indicator of the level of health in a country. The relative frequency histogram below shows the distribution of estimated infant death rates for 224 countries in 2014.
 1 
CIA Factbook, Country Comparison, 2014.
  1. Estimate Q1, the median, and Q3 from the histogram.
  2. Would you expect the mean of this data set to be smaller or larger than the median? Explain your reasoning.

3. TV watchers.

Students in an AP Statistics class were asked how many hours of television they watch per week (including online streaming). This sample yielded an average of 4.71 hours, with a standard deviation of 4.18 hours. Is the distribution of number of hours students watch television weekly symmetric? If not, what shape would you expect this distribution to have? Explain your reasoning.
Solution.
No, we would expect this distribution to be right skewed. There are two reasons for this: (1) there is a natural boundary at 0 (it is not possible to watch less than 0 hours of TV), (2) the standard deviation of the distribution is very large compared to the mean.

4. A new statistic.

The statistic \(\frac{\bar{x}}{median}\) can be used as a measure of skewness. Suppose we have a distribution where all observations are greater than 0, \(x_{i} \gt 0\text{.}\) What is the expected shape of the distribution under the following conditions? Explain your reasoning.
  1. \(\displaystyle \frac{\bar{x}}{median} = 1\)
  2. \(\displaystyle \frac{\bar{x}}{median} \lt 1\)
  3. \(\displaystyle \frac{\bar{x}}{median} \gt 1\)

5. Oscar winners.

The first Oscar awards for best actor and best actress were given out in 1929. The histograms below show the age distribution for all of the best actor and best actress winners from 1929 to 2018. Summary statistics for these distributions are also provided. Compare the distributions of ages of best actor and actress winners
 2 
Oscar winners from 1929-2018, data up to 2009 from the Journal of Statistics Education data archive and for more current data from wikipedia.org/
Best Actress
Mean 36.2
SD 11.9
n 92
Best Actor
Mean 43.8
SD 8.83
n 92
Solution.
The distribution of ages of best actress winners are right skewed with a median around 30 years. The distribution of ages of best actress winners is also right skewed, though less so, with a median around 40 years. The difference between the peaks of these distributions suggest that best actress winners are typically younger than best actor winners. The ages of best actress winners are more variable than the ages of best actor winners. There are potential outliers on the higher end of both of the distributions.

6. Exam scores.

The average on a history exam (scored out of 100 points) was 85, with a standard deviation of 15. Is the distribution of the scores on this exam symmetric? If not, what shape would you expect this distribution to have? Explain your reasoning.

7. Stats scores.

Below are the final exam scores of twenty introductory statistics students.
57 66 69 71 72 73 74 77 78 78 79 81 81 82 83 83 88 89 94
Create a box plot of the distribution of these scores. The five number summary provided below may be useful.
Min Q1 Q2 (Median) Q3 Max
57 72.5 78.5 82.5 94
Solution.

8. Marathon winners.

The histogram and box plots below show the distribution of finishing times for male and female winners of the New York Marathon between 1970 and 1999.
  1. What features of the distribution are apparent in the histogram and not the box plot? What features are apparent in the box plot but not in the histogram?
  2. What may be the reason for the bimodal distribution? Explain.
  3. Compare the distribution of marathon times for men and women based on the box plot shown below.
  4. The time series plot shown below is another way to look at these data. Describe what is visible in this plot but not in the others.

9. Birth Weight.

In a large study of birth weight of newborns, the weights of 23,419 newborn boys were recorded. The distribution of weights was approximately normal with a mean of 7.44 lbs (3376 grams) and a standard deviation of 1.33 lbs (603 grams). The government classifies a newborn as having low birth weight if the weight is less than 5.5 pounds.
 3 
www.biomedcentral.com/1471-2393/8/5
  1. What percent of these newborns had a low birth weight?
  2. Approximately what percent of these babies weighed greater than 10 pounds?
  3. Approximately how many of these newborns weighed greater than 10 pounds?
  4. How much would a newborn have to weigh in order to be at the 90th percentile among this group?
Solution.
  1. \(Z=\frac{5.5-7.44}{1.33}= -1.49\text{;}\) \(P(Z \lt -1.49) = 0.068\text{.}\) Approximately 6.8% of the newborns were of low birth weight.
  2. \(Z=\frac{10-7.44}{1.33}= 1.925\text{.}\) Using a lower bound of 2 and an upper bound of 5, we get \(P(Z \gt 1.925) = 0.027\text{.}\) Approximately 2.7% of the newborns weighed over 10 pounds.
  3. Approximately 2.7% of the newborns weighed over 10 pounds. Because there were 23,419 of them, about \(0.027 \times 23419 \approx 632\) weighed greater than 10 pounds.
  4. Because we have the percentile, this is the inverse problem. To get the Z-score, use the inverse normal option with 0.90 to get \(Z=1.28\text{.}\) Then solve for \(x\) in \(1.28=Z=\frac{x-7.44}{1.33}\) to get \(x=9.15\text{.}\) To be at the 90th percentile among this group, a newborn would have to weigh 9.15 pounds.

10. Auto insurance premiums.

Suppose a newspaper article states that the distribution of auto insurance premiums for residents of California is approximately normal with a mean of $1,650. The article also states that 25% of California residents pay more than $1,800.
  1. What is the \(Z\)-score that corresponds to the top 25% (or the \(75^{\text{th}}\) percentile) of the standard normal distribution?
  2. What is the mean insurance cost? What is the cutoff for the \(75^{\text{th}}\) percentile?
  3. Identify the standard deviation of insurance premiums in California.

11. Speeding on the I-5, Part I.

The distribution of passenger vehicle speeds traveling on the Interstate 5 Freeway (I-5) in California is nearly normal with a mean of 72.6 miles/hour and a standard deviation of 4.78 miles/hour.
 4 
S. Johnson and D. Murray. “Empirical Analysis of Truck and Automobile Speeds on Rural Interstates: Impact of Posted Speed Limits”. In: Transportation Research Board 89th Annual Meeting. 2010.
  1. What percent of passenger vehicles travel slower than 80 miles/hour?
  2. What percent of passenger vehicles travel between 60 and 80 miles/hour?
  3. How fast do the fastest 5% of passenger vehicles travel?
  4. The speed limit on this stretch of the I-5 is 70 miles/hour. Approximate what percentage of the passenger vehicles travel above the speed limit on this stretch of the I-5.
Solution.
  1. 93.94%.
  2. 93.53%.
  3. 80.49 miles/hour.
  4. 70.54%.

12. Heights of 10 year olds, Part I.

Heights of 10 year olds, regardless of gender, closely follow a normal distribution with mean 55 inches and standard deviation 6 inches.
  1. What is the probability that a randomly chosen 10 year old is shorter than 48 inches?
  2. What is the probability that a randomly chosen 10 year old is between 60 and 65 inches?
  3. If the tallest 10% of the class is considered “very tall”, what is the height cutoff for “very tall”?
You have attempted of activities on this page.
PrevTopNext