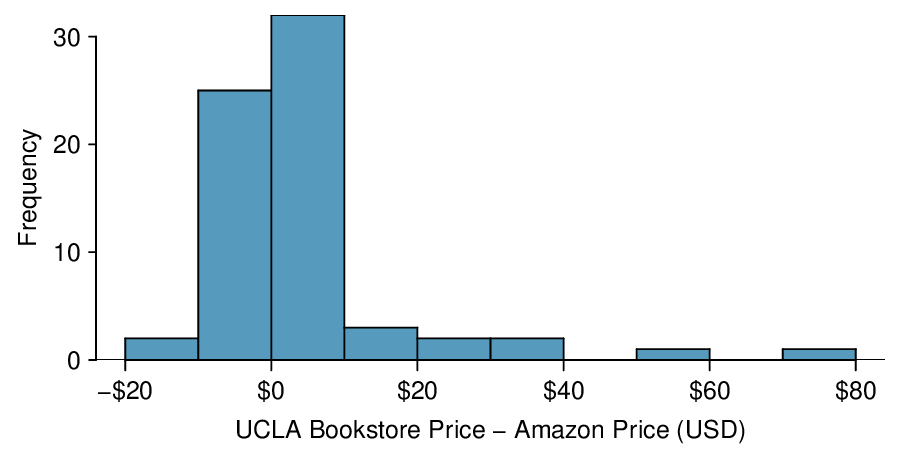
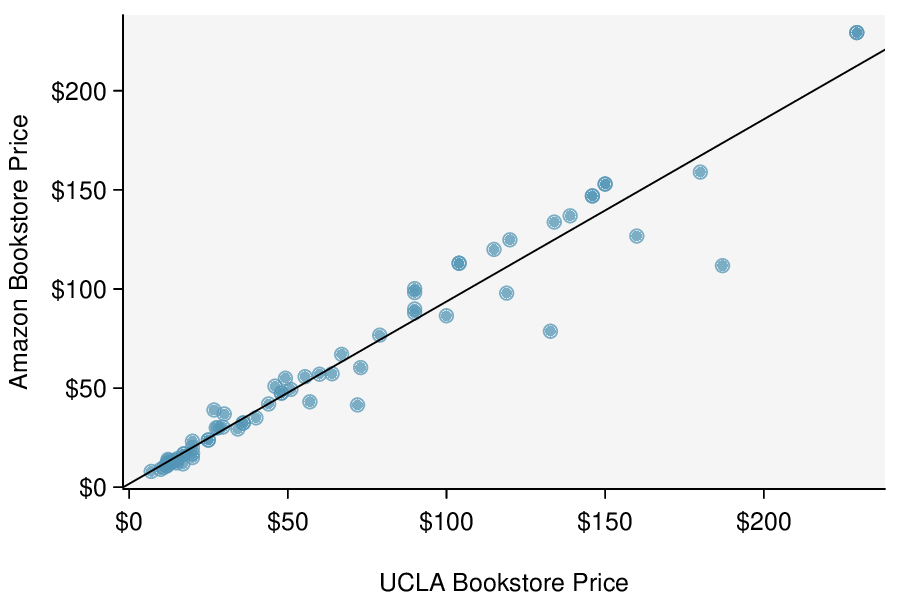
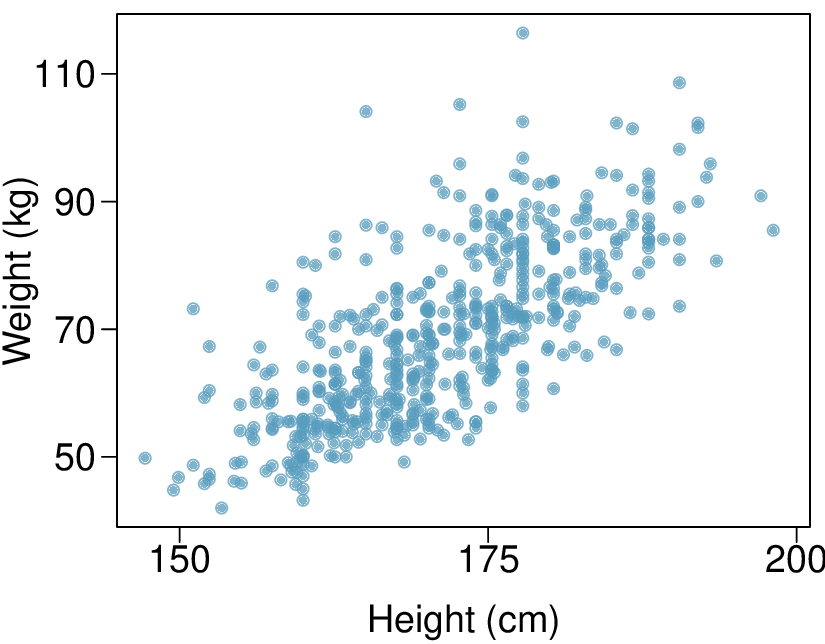
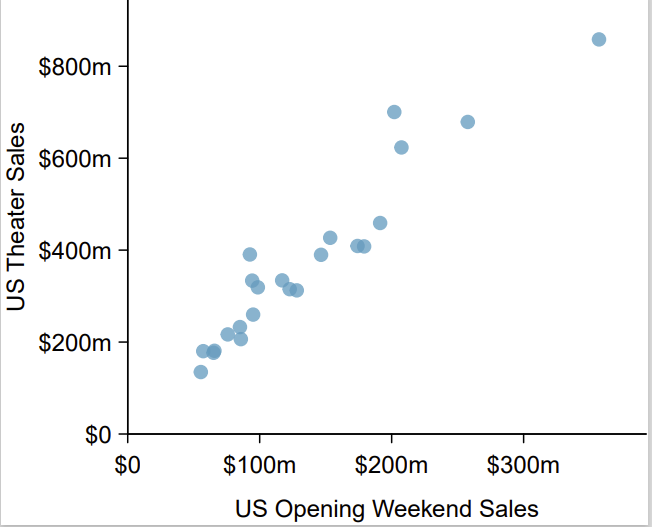
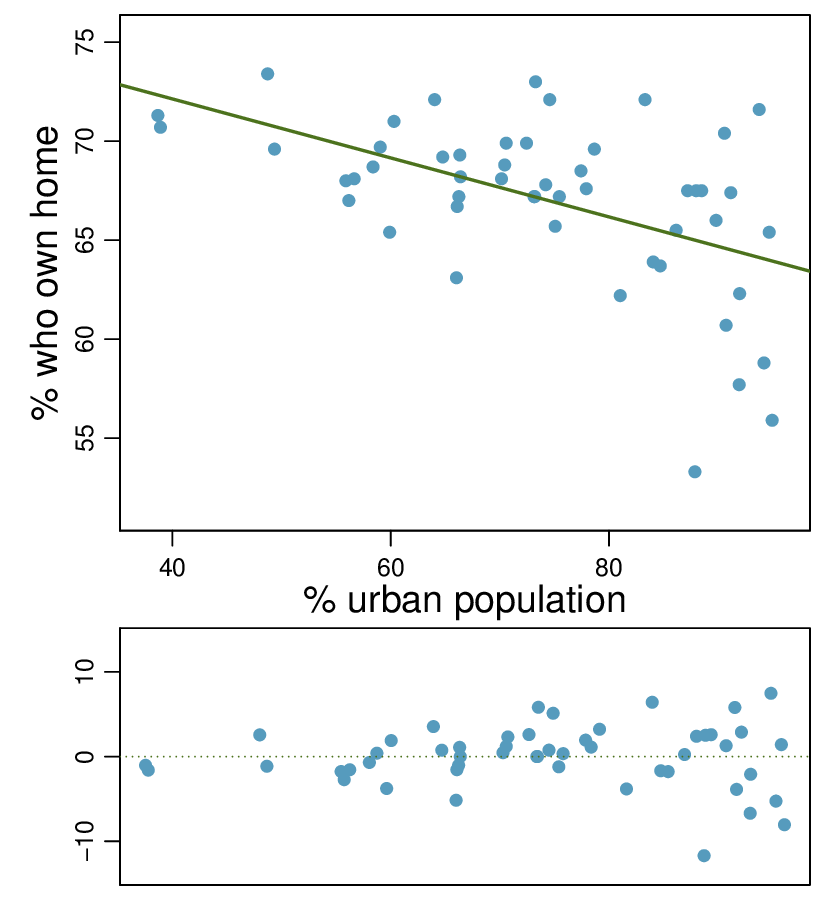
Identify: We will test the following hypotheses at the \(\alpha=0.05\) significance level.
\(H_0\text{:}\) \(\beta = 0\text{.}\) There is no linear relationship.
\(H_A\text{:}\) \(\beta \lt 0\text{.}\) There is a negative linear relationship.
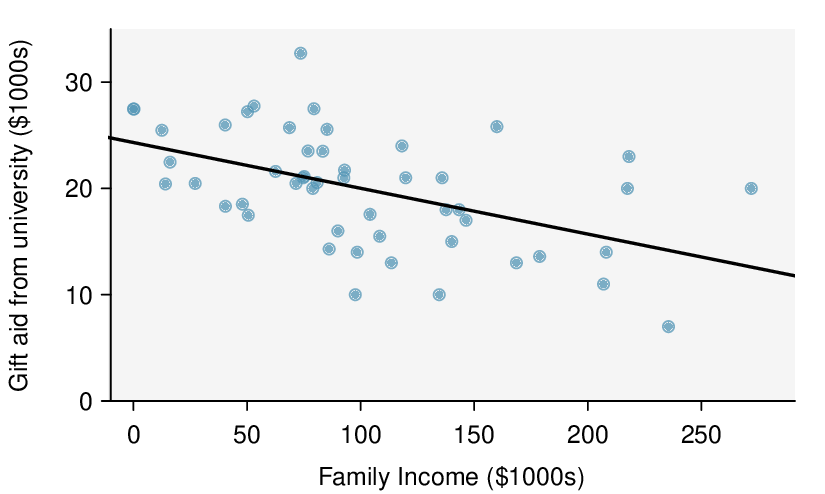
Here, \(\beta\) is the slope of the population regression line for predicting gift aid from family income at Elmhurst College.
Choose: Because the hypotheses are about the slope of a regression line, we choose the \(t\)-test for a slope.
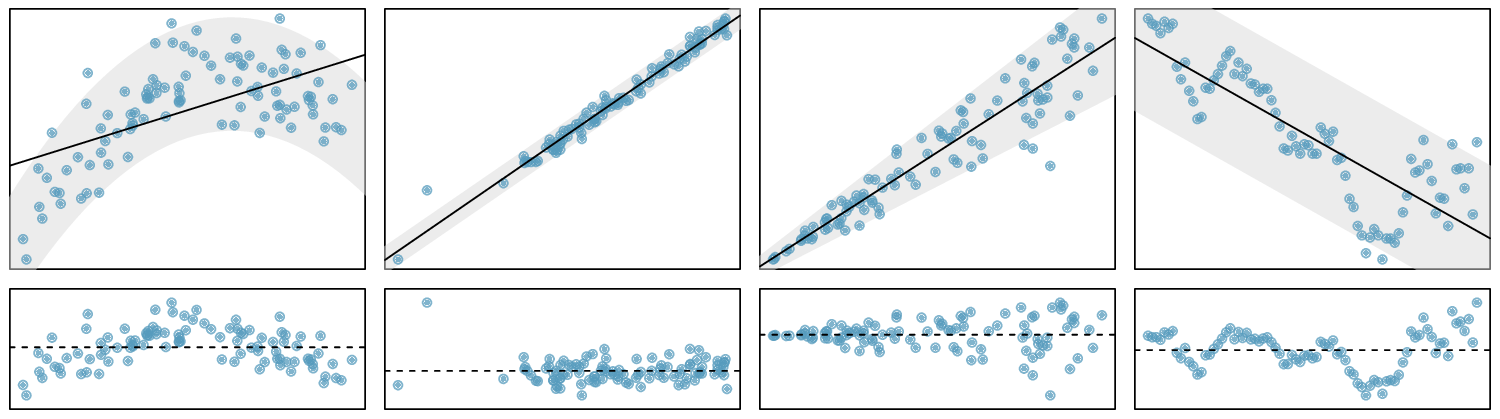
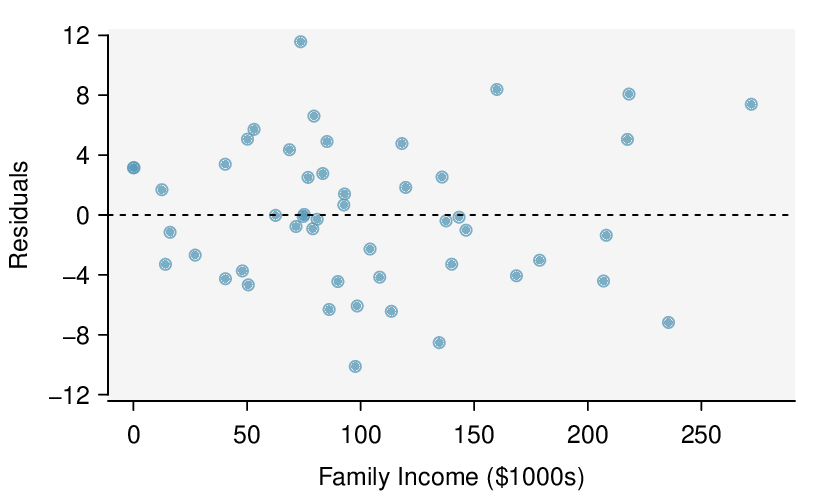
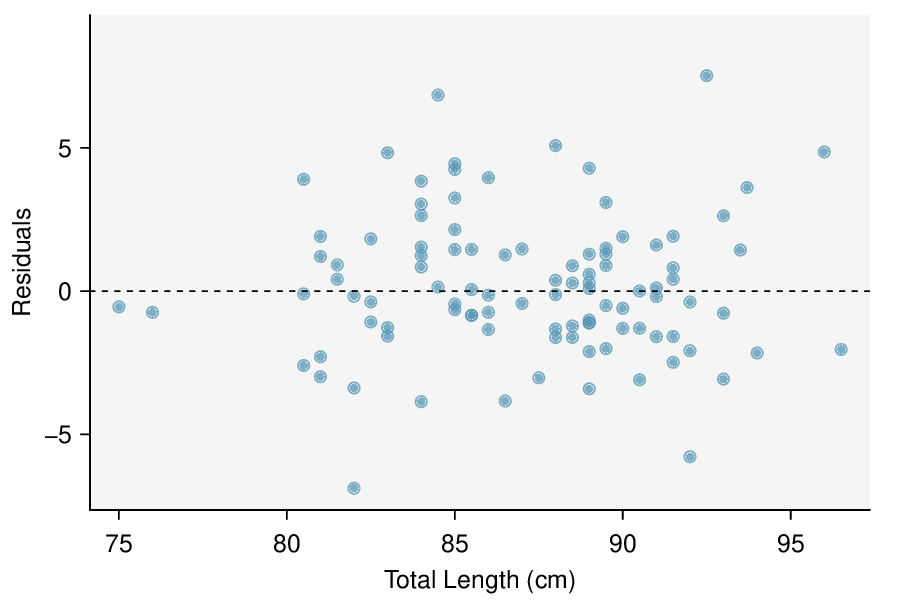
Check: The data come from a random sample of less than 10% of the total population of freshman students at Elmhurst College. The lack of any pattern in the residual plot indicates that a linear model is reasonable. Also, the residual plot shows that the residuals have constant variance. Finally, \(n=50\ge 30\)). so we do not have to worry too much about any skew in the residuals. All four conditions are met.
We read the slope of the sample regression line and the corresponding \(SE\) from the table.
The point estimate is: \(b = -0.04307\text{.}\)
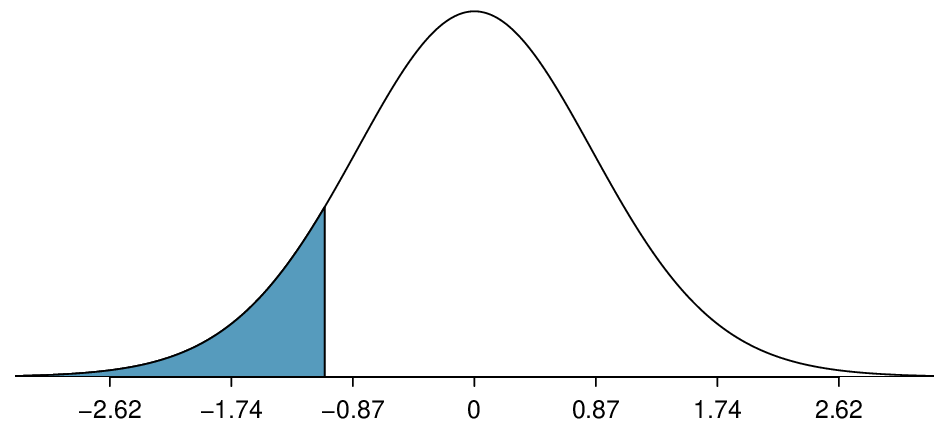
Because \(H_A\) uses a less than sign (\(\lt\)), meaning that it is a lower-tail test, the p-value is the area to the left of \(t=-3.985\) under the \(t\)-distribution with \(50-2=48\) degrees of freedom. The p-value = \(\frac{1}{2}(0.000229)\approx 0.0001\text{.}\)
Conclude: The p-value of 0.0001 is \(\lt 0.05\text{,}\) so we reject \(H_0\text{;}\) there is sufficient evidence that there is a negative linear relationship between family income and gift aid at Elmhurst College.