Skip to main content

Advanced High School Statistics Third Edition

David M Diez, Mine Çetinkaya-Rundel, Leah Dorazio, Christopher D Barr

Section 8.2 Fitting a line by least squares regression

In this section, we answer the following questions:
  • How well can we predict financial aid based on family income for a particular college?
    🔗
    🔗
  • How does one find, interpret, and apply the least squares regression line?
    🔗
    🔗
  • How do we measure the fit of a model and compare different models to each other?
    🔗
    🔗
  • Why do models sometimes make predictions that are ridiculous or impossible?
    🔗
    🔗
🔗

Subsection 8.2.1 An objective measure for finding the best line

Fitting linear models by eye is open to criticism since it is based on an individual preference. In this section, we use least squares regression as a more rigorous approach.
🔗
This section considers family income and gift aid data from a random sample of fifty students in the freshman class of Elmhurst College in Illinois.
 1 
These data were sampled from a table of data for all freshmen from the 2011 class at Elmhurst College that accompanied an article titled What Students Really Pay to Go to College published online by The Chronicle of Higher Education chronicle.com/article/What-Students-Really-Pay-to-Go/131435
Gift aid is financial aid that does not need to be paid back, as opposed to a loan. A scatterplot of the data is shown in Figure 8.2.1 along with two linear fits. The lines follow a negative trend in the data; students who have higher family incomes tended to have lower gift aid from the university.
🔗
Figure 8.2.1. Gift aid and family income for a random sample of 50 freshman students from Elmhurst College. Two lines are fit to the data, the solid line being the least squares line.
🔗
We begin by thinking about what we mean by “best”. Mathematically, we want a line that has small residuals. Perhaps our criterion could minimize the sum of the residual magnitudes:
\begin{gather} |y_1 - \hat{y}_1| + |y_2-\hat{y}_2| + \dots + |y_n-\hat{y}_n|\tag{8.2.1} \end{gather}
which we could accomplish with a computer program. The resulting dashed line shown in Figure 8.2.1 demonstrates this fit can be quite reasonable. However, a more common practice is to choose the line that minimizes the sum of the squared residuals:
\begin{gather} (y_1 - \hat{y}_1)^2 + (y_2-\hat{y}_2)^2+ \dots + (y_n-\hat{y}_n)^2\tag{8.2.2} \end{gather}
🔗
The line that minimizes the sum of the squared residuals is represented as the solid line in Figure 8.2.1. This is commonly called the least squares line.
🔗
Both lines seem reasonable, so why do data scientists prefer the least squares regression line? One reason is that it is easier to compute by hand and in most statistical software. Another, and more compelling, reason is that in many applications, a residual twice as large as another residual is more than twice as bad. For example, being off by 4 is usually more than twice as bad as being off by 2. Squaring the residuals accounts for this discrepancy.
🔗
In Figure 8.2.2, we imagine the squared error about a line as actual squares. The least squares regression line minimizes the sum of the areas of these squared errors. In the figure, the sum of the squared error is \(4+1+1=6\text{.}\) There is no other line about which the sum of the squared error will be smaller.
🔗
Figure 8.2.2. A visualization of least squares regression using Desmos. Try out this and other interactive Desmos activities at openintro.org/ahss/desmos
 2 
teacher.desmos.com/collection/5cae8f9c0924751e461dd6f7
.
🔗
🔗

Subsection 8.2.2 Finding the least squares line

For the Elmhurst College data, we could fit a least squares regression line for predicting gift aid based on a student’s family income and write the equation as:
\begin{gather*} \widehat{\text{aid}} = a + b\times \text{family income} \end{gather*}
🔗
Here \(a\) is the \(y\)-intercept of the least squares regression line and \(b\) is the slope of the least squares regression line. \(a\) and \(b\) are both statistics that can be calculated from the data. In the next section we will consider the corresponding parameters that they statistics attempt to estimate.
🔗
We can enter all of the data into a statistical software package and easily find the values of \(a\) and \(b\text{.}\) However, we can also calculate these values by hand, using only the summary statistics.
  • The slope of the least squares line is given by
    \begin{gather} b = r\frac{s_y}{s_x}\tag{8.2.3} \end{gather}
    where \(r\) is the correlation between the variables \(x\) and \(y\text{,}\) and \(s_x\) and \(s_y\) are the sample standard deviations of \(x\text{,}\) the explanatory variable, and \(y\text{,}\) the response variable.
    🔗
    🔗
  • The point of averages \((\bar{x}, \bar{y})\) is always on the least squares line. Plugging this point in for \(x\) and \(y\) in the least squares equation and solving for \(a\) gives
    \begin{align*} \bar{y} \amp = a + b\bar{x} \amp \amp a=\bar{y}-b\bar{x} \end{align*}
    🔗
    🔗
🔗

Finding the slope and intercept of the least squares regression line.

The least squares regression line for predicting \(y\) based on \(x\) can be written as: \(\hat{y}=a+bx\text{.}\)
\begin{gather*} b=r\frac{s_y}{s_x} \qquad \bar{y} = a + b\bar{x} \end{gather*}
🔗
We first find \(b\text{,}\) the slope, and then we solve for \(a\text{,}\) the \(y\)-intercept.
🔗
🔗

Guided Practice 8.2.3.

Table 8.2.4 shows the sample means for the family income and gift aid as $101,800 and $19,940, respectively. Plot the point \((101.8, 19.94)\) on Figure 8.2.1 to verify it falls on the least squares line (the solid line).
 3 
If you need help finding this location, draw a straight line up from the x-value of 100 (or thereabout). Then draw a horizontal line at 20 (or thereabout). These lines should intersect on the least squares line.
🔗
🔗
Table 8.2.4. Summary statistics for family income and gift aid.
🔗
family income, in $1000s (\(x\)) gift aid, in $1000s (\(y\))
mean \(\bar{x} = 101.8\) \(\bar{y} = 19.94\)
sd \(s_x = 63.2\) \(s_y = 5.46\)
\(r=-0.499\)

Example 8.2.5.

Using the summary statistics in Table 8.2.4, find the equation of the least squares regression line for predicting gift aid based on family income.
🔗
Solution.
\begin{align*} b \amp = r\frac{s_y}{s_x} = (-0.499)\frac{5.46}{63.2} = -0.0431\\ a \amp = \bar{y} - b\bar{x} = 19.94 - (-0.0431)(101.8) = 24.3\\ \hat{y}\amp =24.3 - 0.0431x \qquad\text{ or } \qquad \widehat{\text{aid}} = 24.3 - 0.0431\times \text{family income} \end{align*}
🔗
🔗
🔗

Example 8.2.6.

Say we wanted to predict a student’s family income based on the amount of gift aid that they received. Would this least squares regression line be the following?
\begin{gather*} \text{aid} = 24.3 - 0.0431\times \widehat{\text{family income}} \end{gather*}
🔗
Solution.
No. The equation we found was for predicting aid, not for predicting family income. We would have to calculate a new regression line, letting \(y\) be \(\text{family income}\) and \(x\) be \(\text{aid}\text{.}\) This would give us:
\begin{align*} b \amp = r\frac{s_y}{s_x} = (-0.499)\frac{63.2}{5.46} = -5.776\\ a \amp = \bar{y} - b\bar{x} = 19.94 - (-5.776)(101.8) = 607.9\\ \hat{y}\amp =607.3 - 5.776x \qquad\text{ or } \qquad \widehat{\text{family income}} = 607.3 - 5.776\times \text{aid} \end{align*}
🔗
🔗
🔗
We mentioned earlier that a computer is usually used to compute the least squares line. A summary table based on computer output is shown in Table 8.2.7 for the Elmhurst College data. The first column of numbers provides estimates for \({b}_0\) and \({b}_1\text{,}\) respectively. Compare these to the result from Example 8.2.5.
🔗
Table 8.2.7. Summary of least squares fit for the Elmhurst College data. Compare the parameter estimates in the first column to the results of Example 8.2.5.
🔗
Estimate Std. Error t value Pr\((>|t|)\)
(Intercept) 24.3193 1.2915 18.83 0.0000
family_income -0.0431 0.0108 -3.98 0.0002

Example 8.2.8.

Examine the second, third, and fourth columns in Table 8.2.7. Can you guess what they represent?
🔗
Solution.
We’ll look at the second row, which corresponds to the slope. The first column, Estimate = -0.0431, tells us our best estimate for the slope of the population regression line. We call this point estimate \(b\text{.}\) The second column, Std. Error = 0.0108, is the standard error of this point estimate. The third column, t value = -3.98, is the \(T\) test statistic for the null hypothesis that the slope of the population regression line = 0. The last column, Pr\((>|t|) = 0.0002\text{,}\) is the p-value for this two-sided \(T\)-test. We will get into more of these details in Section 8.4.
🔗
🔗
🔗

Example 8.2.9.

Suppose a high school senior is considering Elmhurst College. Can she simply use the linear equation that we have found to calculate her financial aid from the university?
🔗
Solution.
No. Using the equation will provide a prediction or estimate. However, as we see in the scatterplot, there is a lot of variability around the line. While the linear equation is good at capturing the trend in the data, there will be significant error in predicting an individual student’s aid. Additionally, the data all come from one freshman class, and the way aid is determined by the university may change from year to year.
🔗
🔗
🔗
🔗

Subsection 8.2.3 Interpreting the coefficients of a regression line

Interpreting the coefficients in a regression model is often one of the most important steps in the analysis.
🔗

Example 8.2.10.

The slope for the Elmhurst College data for predicting gift aid based on family income was calculated as -0.0431. Intepret this quantity in the context of the problem.
🔗
Solution.
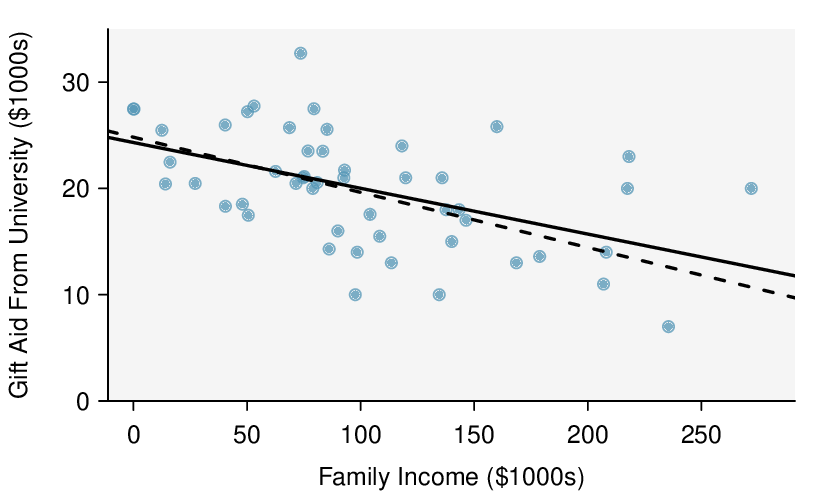
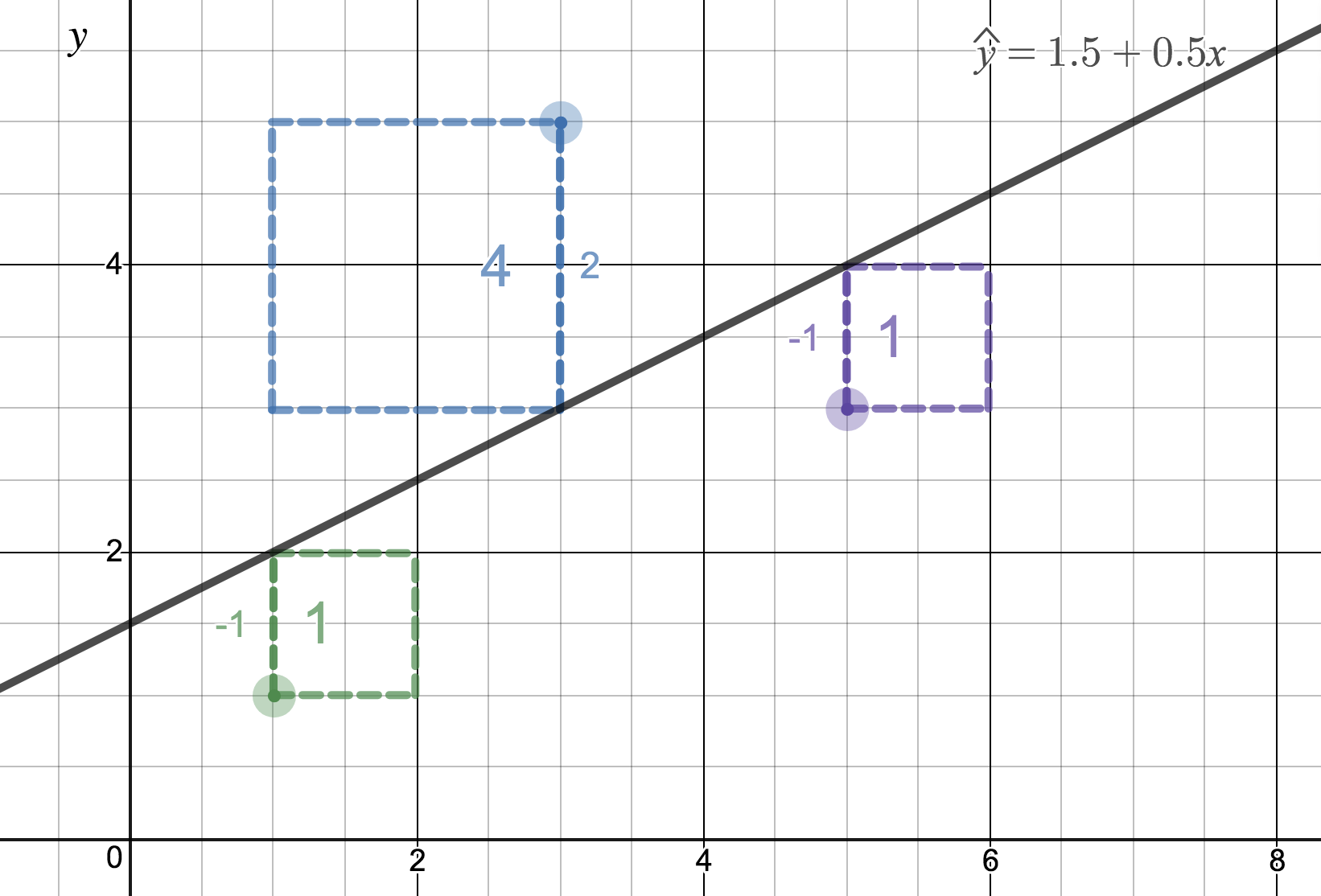
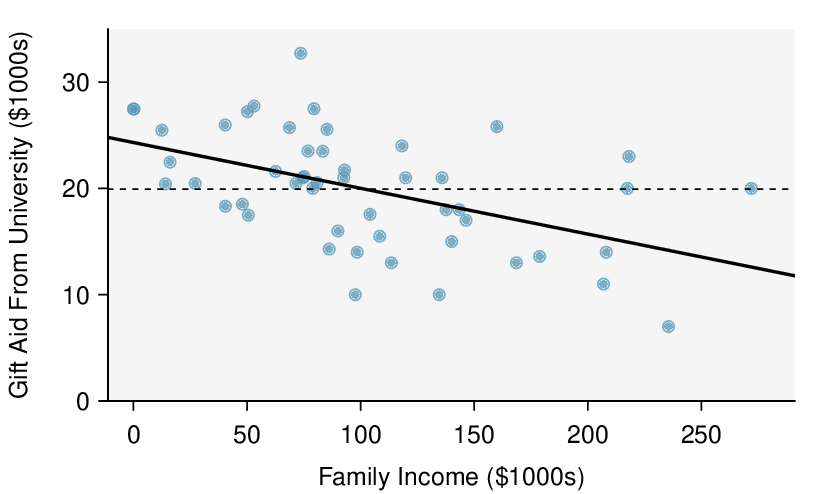
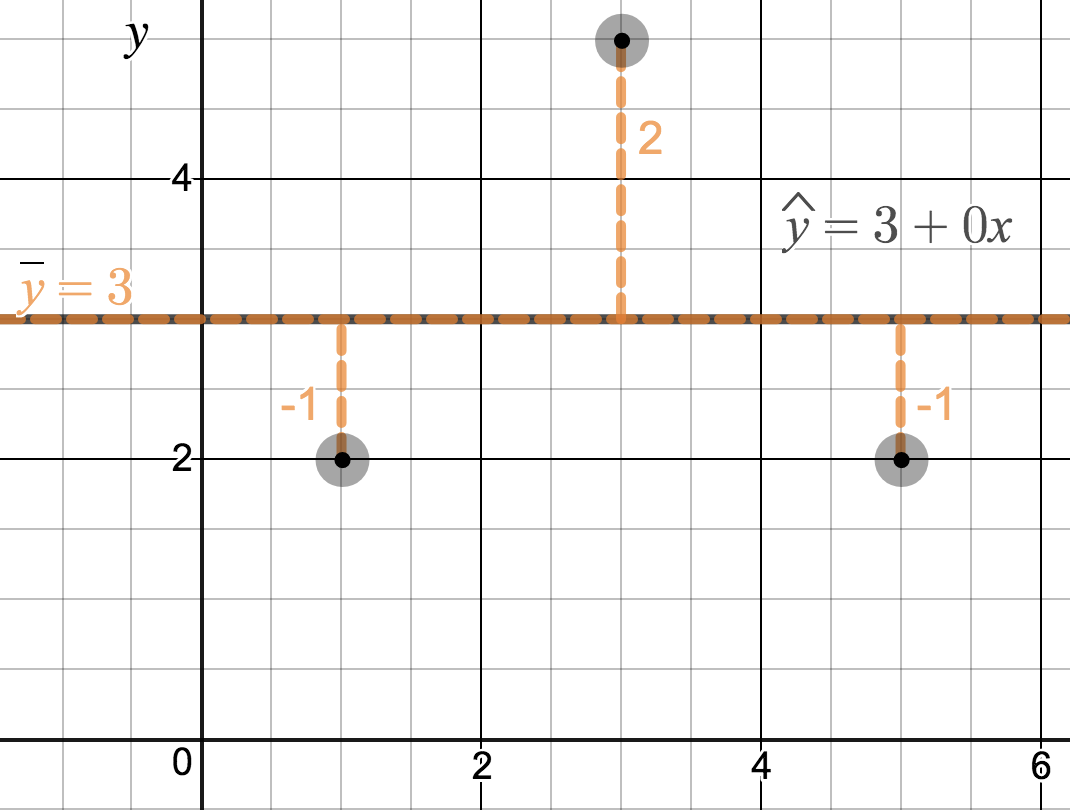
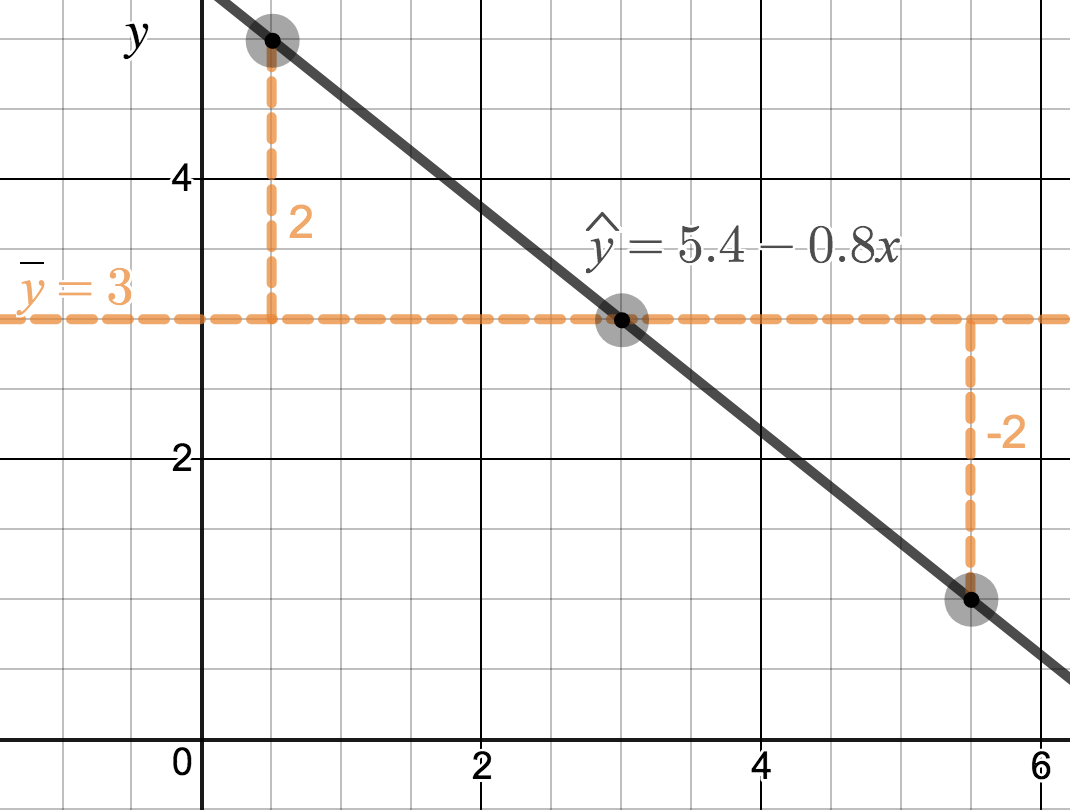
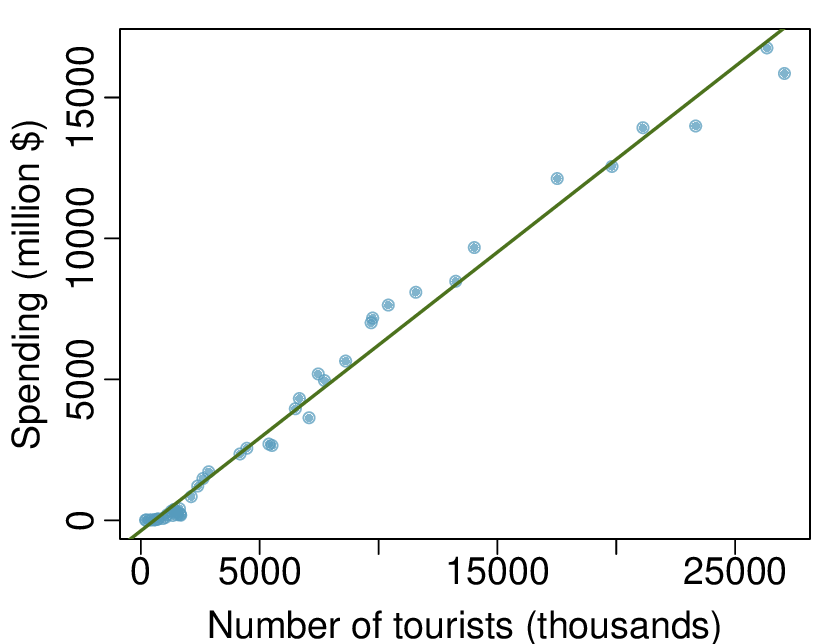
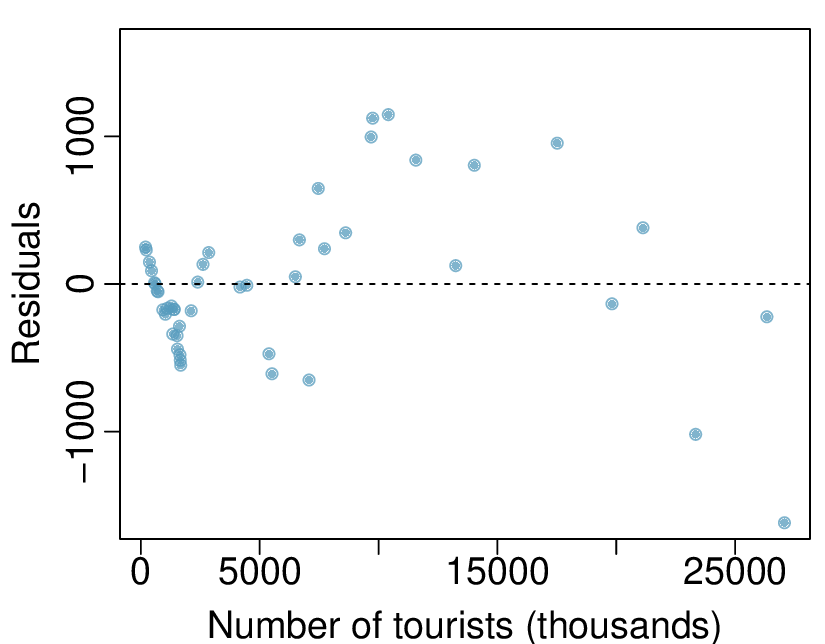
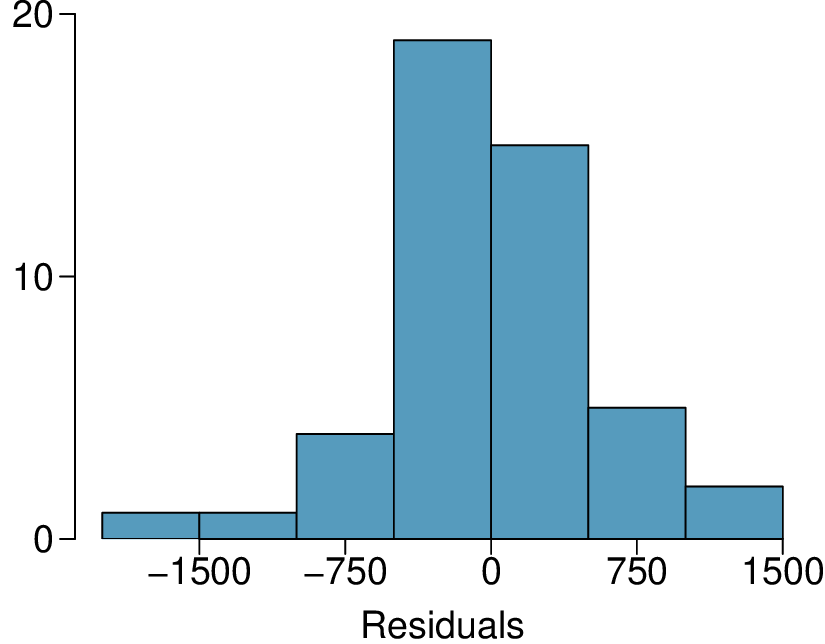
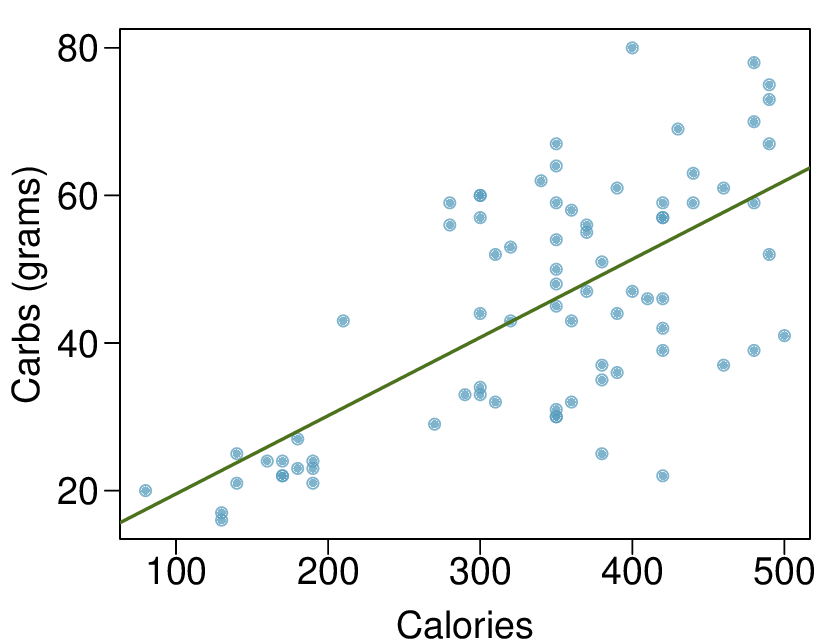
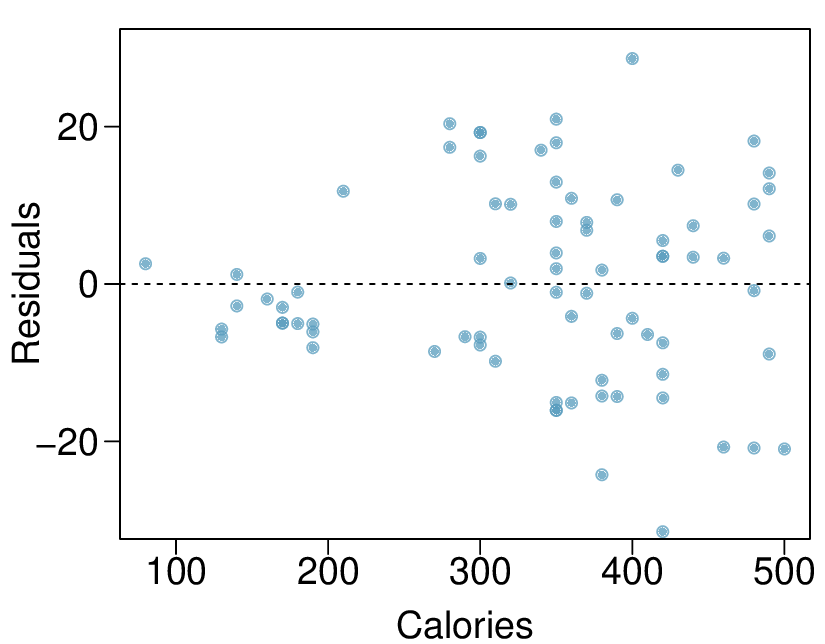
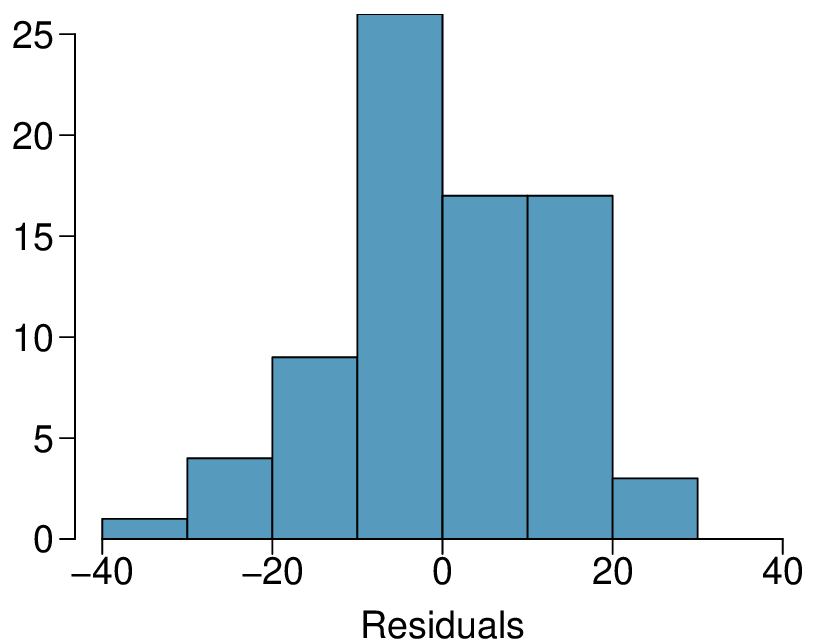
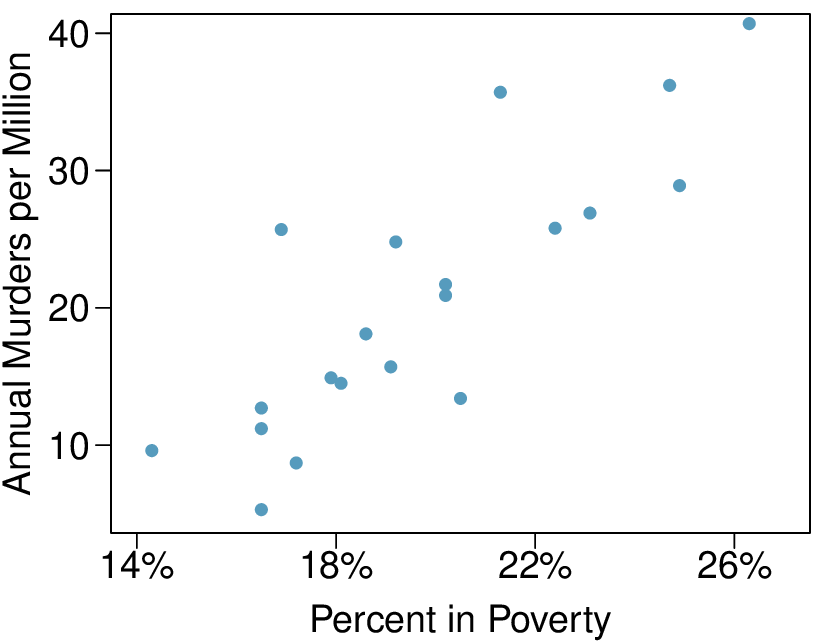
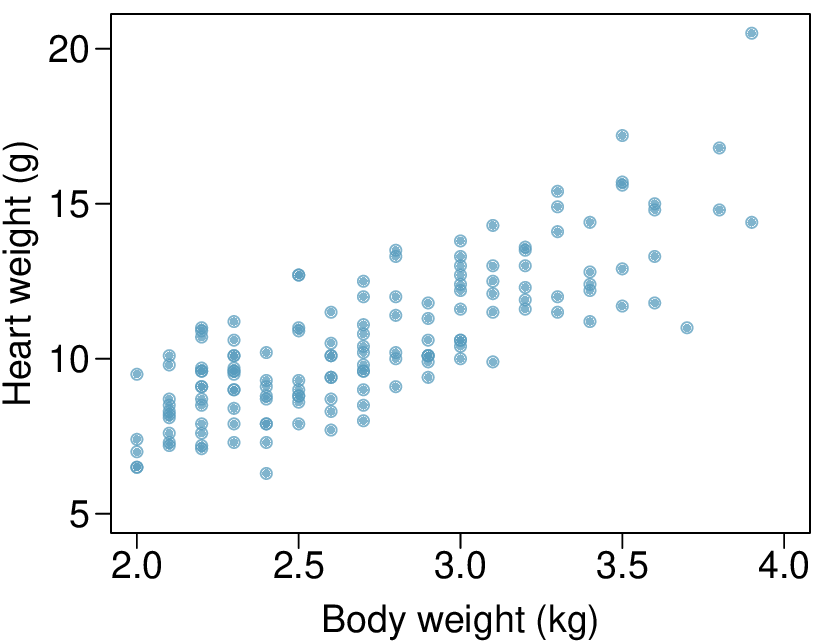
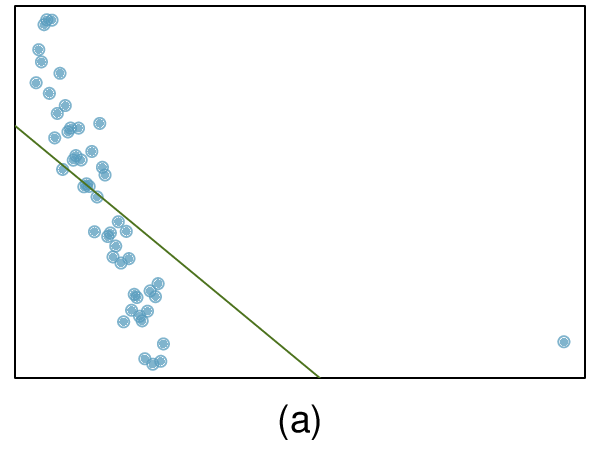
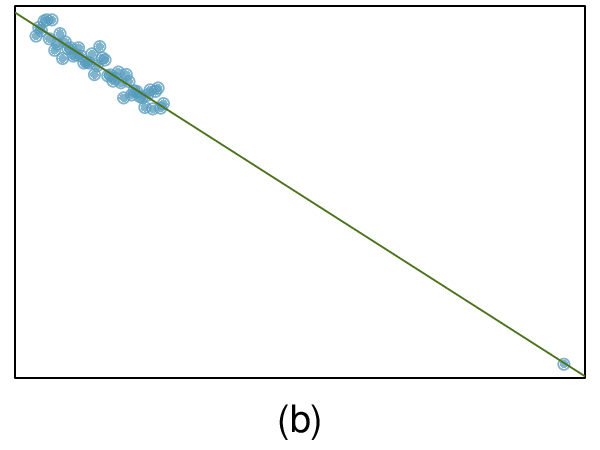
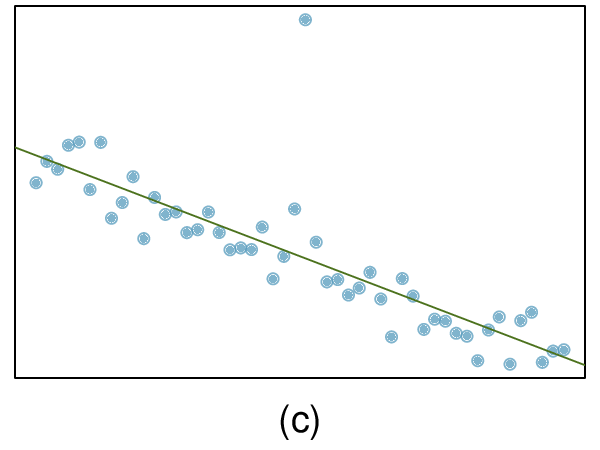
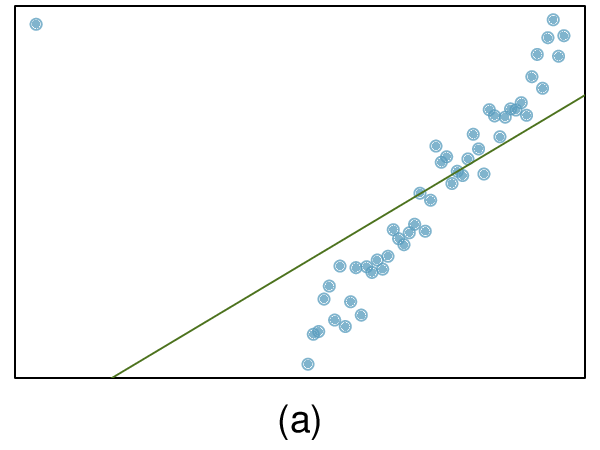
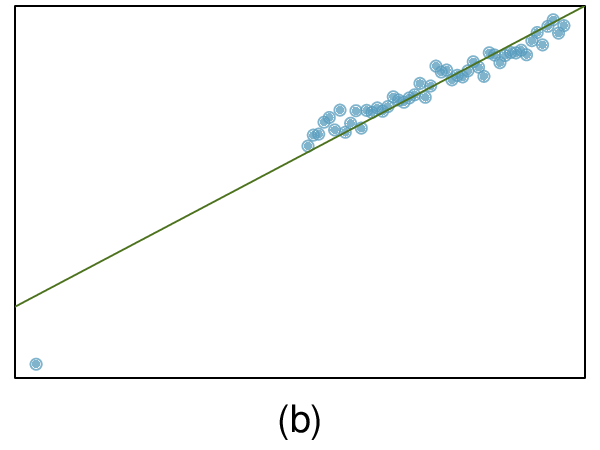
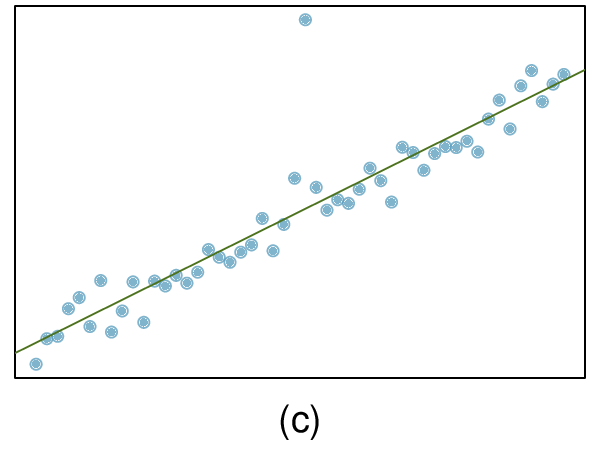
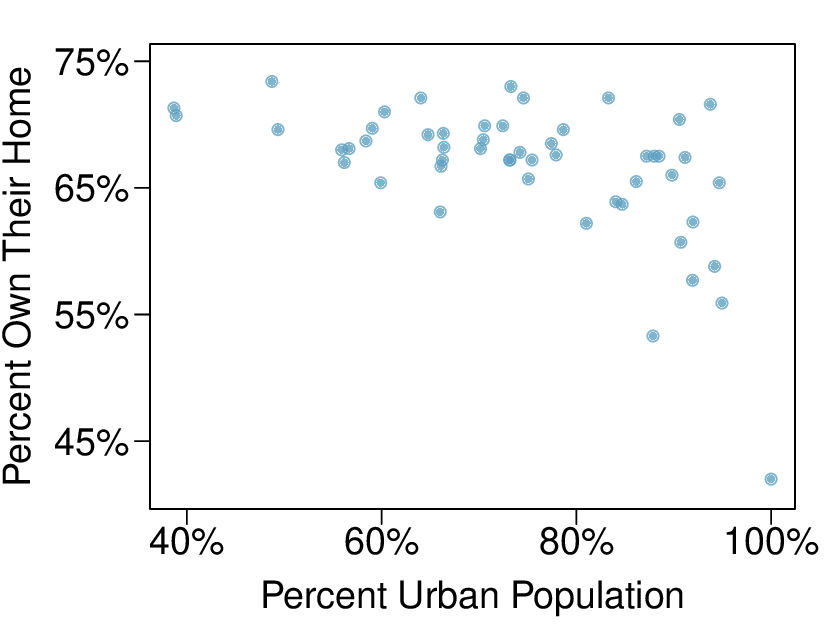
You might recall from an algebra course that slope is change in \(y\) over change in \(x\text{.}\) Here, both \(x\) and \(y\) are in thousands of dollars. So if \(x\) is one unit or one thousand dollars higher, the line will predict that \(y\) will change by 0.0431 thousand dollars. In other words, for each additional thousand dollars of family income, on average, students receive 0.0431 thousand, or $43.10 less in gift aid. Note that a higher family income corresponds to less aid because the slope is negative.
🔗
🔗
🔗

Example 8.2.11.

The \(y\)-intercept for the Elmhurst College data for predicting gift aid based on family income was calculated as 24.3. Intepret this quantity in the context of the problem.
🔗
Solution.
The intercept \(a\) describes the predicted value of \(y\) when \(x=0\text{.}\) The predicted gift aid is 24.3 thousand dollars if a student’s family has no income. The meaning of the intercept is relevant to this application since the family income for some students at Elmhurst is $0. In other applications, the intercept may have little or no practical value if there are no observations where \(x\) is near zero. Here, it would be acceptable to say that the average gift aid is 24.3 thousand dollars among students whose family have 0 dollars in income.
🔗
🔗
🔗

Interpreting coefficients in a linear model.

  • The slope, \(b\text{,}\) describes the average increase or decrease in the \(y\) variable if the explanatory variable \(x\) is one unit larger.
    🔗
    🔗
  • The y-intercept, \(a\text{,}\) describes the predicted outcome of \(y\) if \(x=0\text{.}\) The linear model must be valid all the way to \(x=0\) for this to make sense, which in many applications is not the case.
    🔗
    🔗
🔗
🔗

Guided Practice 8.2.12.

In the previous chapter, we encountered a data set that compared the price of new textbooks for UCLA courses at the UCLA Bookstore and on Amazon. We fit a linear model for predicting price at UCLA Bookstore from price on Amazon and we get:
\begin{gather*} \hat{y} = 1.86 + 1.03x \end{gather*}
where \(x\) is the price on Amazon and \(y\) is the price at the UCLA bookstore. Interpret the coefficients in this model and discuss whether the interpretations make sense in this context.
 4 
The \(y\)-intercept is 1.86 and the units of \(y\) are in dollars. This tells us that when a textbook costs 0 dollars on Amazon, the predicted price of the textbook at the UCLA Bookstore is 1.86 dollars. This does not make sense as Amazon does not sell any $0 textbooks. The slope is 1.03, with units (dollars)/(dollars). On average, for every extra dollar that a book costs on Amazon, it costs an extra 1.03 dollars at the UCLA Bookstore. This interpretation does make sense in this context.
🔗
🔗

Guided Practice 8.2.13.

Can we conclude that if Amazon raises the price of a textbook by 1 dollar, the UCLA Bookstore will raise the price of the textbook by $1.03?
 5 
No. The slope describes the overall trend. This is observational data; a causal conclusion cannot be drawn. Remember, a causal relationship can only be concluded by a well-designed randomized, controlled experiment. Additionally, there may be large variation in the points about the line. The slope does not tell us how much \(y\) might change based on a change in \(x\) for a particular textbook.
🔗
🔗

Exercise caution when interpreting coefficients of a linear model.

  • The slope tells us only the average change in \(y\) for each unit change in \(x\text{;}\) it does not tell us how much \(y\) might change based on a change in \(x\) for any particular individual. Moreover, in most cases, the slope cannot be interpreted in a causal way.
    🔗
    🔗
  • When a value of \(x=0\) doesn’t make sense in an application, then the interpretation of the \(y\)-intercept won’t have any practical meaning.
    🔗
    🔗
🔗
🔗
🔗

Subsection 8.2.4 Extrapolation is treacherous

When those blizzards hit the East Coast this winter, it proved to my satisfaction that global warming was a fraud. That snow was freezing cold. But in an alarming trend, temperatures this spring have risen. Consider this: On February \(6^{th}\) it was 10 degrees. Today it hit almost 80. At this rate, by August it will be 220 degrees. So clearly folks the climate debate rages on.
🔗
―Stephen Colbert
April 6th, 2010
Video Link: www.cc.com/video-clips/l4nkoq/
 6 
www.cc.com/video-clips/l4nkoq/the-colbert-report-science-catfight---joe-bastardi-vs--brenda-ekwurzel
🔗
Linear models can be used to approximate the relationship between two variables. However, these models have real limitations. Linear regression is simply a modeling framework. The truth is almost always much more complex than our simple line. For example, we do not know how the data outside of our limited window will behave.
🔗

Example 8.2.14.

Use the model \(\widehat{\text{aid}} = 24.3 - 0.0431\times \text{family income}\) to estimate the aid of another freshman student whose family had income of $1 million.
🔗
Solution.
Recall that the units of family income are in $1000s, so we want to calculate the aid for \(\text{family income}= 1000\text{:}\)
\begin{align*} \widehat{\text{aid}} \amp = 24.3 - 0.0431 \times \text{family income}\\ \widehat{\text{aid}}\amp =24.3 - 0.431(1000) = -18.8 \end{align*}
🔗
The model predicts this student will have -$18,800 in aid (!). Elmhurst College cannot (or at least does not) require any students to pay extra on top of tuition to attend.
🔗
🔗
🔗
Using a model to predict \(y\)-values for \(x\)-values outside the domain of the original data is called extrapolation. Generally, a linear model is only an approximation of the real relationship between two variables. If we extrapolate, we are making an unreliable bet that the approximate linear relationship will be valid in places where it has not been analyzed.
🔗
🔗

Subsection 8.2.5 Using \(R^2\) to describe the strength of a fit

We evaluated the strength of the linear relationship between two variables earlier using the correlation, \(r\text{.}\) However, it is more common to explain the fit of a model using \(R^2\text{,}\) called R-squared or the explained variance. If provided with a linear model, we might like to describe how closely the data cluster around the linear fit.
🔗
Figure 8.2.15. Gift aid and family income for a random sample of 50 freshman students from Elmhurst College, shown with the least squares regression line (\(\hat{y}\)) and the average line (\(\bar{y}\)).
🔗
We are interested in how well a model accounts for or explains the location of the \(y\) values. The \(R^2\) of a linear model describes how much smaller the variance (in the \(y\) direction) about the regression line is than the variance about the horizontal line \(\bar{y}\text{.}\) For example, consider the Elmhurst College data, shown in Figure 8.2.15. The variance of the response variable, aid received, is \(s_{aid}^2=29.8\text{.}\) However, if we apply our least squares line, then this model reduces our uncertainty in predicting aid using a student’s family income. The variability in the residuals describes how much variation remains after using the model: \(s_{_{RES}}^2 = 22.4\text{.}\) We could say that the reduction in the variance was:
\begin{equation*} \frac{s_{aid}^2 - s_{_{RES}}^2}{s_{aid}^2} = \frac{29.8 - 22.4}{29.8} = \frac{7.5}{29.8} = 0.25 \end{equation*}
🔗
If we used the simple standard deviation of the residuals, this would be exactly \(R^2\text{.}\) However, the standard way of computing the standard deviation of the residuals is slightly more sophisticated.
 7 
In computing the standard deviation of the residuals, we divide by \(n-2\) rather than by \(n-1\) to account for the \(n-2\) degrees of freedom.
To avoid any trouble, we can instead use a sum of squares method. If we call the sum of the squared errors about the regression line \(SSRes\) and the sum of the squared errors about the mean \(SSM\text{,}\) we can define \(R^2\) as follows:
\begin{gather*} R^2=\frac{SSM - SSRes}{SSM} = 1-\frac{SSRes}{SSM} \end{gather*}
🔗
(a)
🔗
(b)
🔗
Figure 8.2.16. In Figure 8.2.16.(a) the regression line is equivalent to \(\bar{y}\text{;}\) \(R^2 = 0\text{.}\) In Figure 8.2.16.(b) the regression line passes through all of the points; \(R^2=1\text{.}\) Try out this and other interactive Desmos activities at openintro.org/ahss/desmos
 8 
teacher.desmos.com/collection/5cae8f9c0924751e461dd6f7
.
🔗

Guided Practice 8.2.17.

Using the formula for \(R^2\text{,}\) confirm that in Figure 8.2.16.(a), \(R^2 = 0\) and that in Figure 8.2.16.(b), \(R^2 = 1\text{.}\)
 9 
(a) \(\text{SSRes }=\text {SSM }= (-1)^2+(2)^2+(-1)^2 = 6\text{,}\) so \(R^2 = 1 -\frac{6}{6}=0\text{.}\) (b) \(R^2= 1- \frac{0}{8}\text{.}\)
🔗
🔗

\(R^2\) is the explained variance.

\(R^2\) is always between 0 and 1, inclusive. It tells us the proportion of variation in the \(y\) values that is explained by a regression model. The higher the value of \(R^2\text{,}\) the better the model “explains” the response variable.
🔗
🔗
The value of \(R^2\) is, in fact, equal to \(r^2\text{,}\) where \(r\) is the correlation. This means that \(r = \pm \sqrt{R^2}\text{.}\) Use this fact to answer the next two practice problems.
🔗

Guided Practice 8.2.18.

If a linear model has a very strong negative relationship with a correlation of -0.97, how much of the variation in the response variable is explained by the linear model?
 10 
\(R^2 = (-0.97)^2 = 0.94\) or 94%. 94% of the variation in \(y\) is explained by the linear model.
🔗
🔗

Guided Practice 8.2.19.

If a linear model has an \(R^2\) or explained variance of 0.94, what is the correlation?
 11 
We take the square root of \(R^2\) and get 0.97, but we must be careful, because \(r\) could be 0.97 or -0.97. Without knowing the slope or seeing the scatterplot, we have no way of knowing if \(r\) is positive or negative.
🔗
🔗
🔗

Subsection 8.2.6 Technology: linear correlation and regression

Get started quickly with this Desmos LinReg Calculator
 12 
www.desmos.com/calculator/84awrx6hxa
(available at openintro.org/ahss/desmos
 13 
www.openintro.org/ahss/desmos
).
🔗
Calculator instructions
🔗

TI-84: finding \(a\text{,}\) \(b\text{,}\) \(R^2\text{,}\) and \(r\) for a linear model.

Use STAT, CALC, LinReg(a + bx).
  1. Choose STAT.
    🔗
    🔗
  2. Right arrow to CALC.
    🔗
    🔗
  3. Down arrow and choose 8:LinReg(a+bx).
    • Caution: choosing 4:LinReg(ax+b) will reverse \(a\) and \(b\text{.}\)
      🔗
      🔗
    🔗
    🔗
  4. Let Xlist be L1 and Ylist be L2 (don’t forget to enter the \(x\) and \(y\) values in L1 and L2 before doing this calculation).
    🔗
    🔗
  5. Leave FreqList blank.
    🔗
    🔗
  6. Leave Store RegEQ blank.
    🔗
    🔗
  7. Choose Calculate and hit ENTER, which returns:
    🔗
    a \(a\text{,}\) the y-intercept of the best fit line
    b \(b\text{,}\) the slope of the best fit line
    \(r^2\) \(R^2\text{,}\) the explained variance
    r \(r\text{,}\) the correlation coefficient
    🔗
🔗
TI-83: Do steps 1-3, then enter the \(x\) list and \(y\) list separated by a comma, e.g. LinReg(a+bx) L1, L2, then hit ENTER.
🔗
🔗

What to do if \(r^2\) and \(r\) do not show up on a TI-83/84.

If \(r^2\) and \(r\) do now show up when doing STAT, CALC, LinReg, the diagnostics must be turned on. This only needs to be once and the diagnostics will remain on.
  1. Hit 2ND 0 (i.e. CATALOG).
    🔗
    🔗
  2. Scroll down until the arrow points at DiagnosticOn.
    🔗
    🔗
  3. Hit ENTER and ENTER again. The screen should now say:
    🔗
    DiagnosticOn
    Done
    🔗
🔗
🔗

What to do if a TI-83/84 returns: ERR: DIM MISMATCH.

This error means that the lists, generally L1 and L2, do not have the same length.
  1. Choose 1:Quit.
    🔗
    🔗
  2. Choose STAT, Edit and make sure that the lists have the same number of entries.
    🔗
    🔗
🔗
🔗

Casio fx-9750GII: finding \(a\text{,}\) \(b\text{,}\) \(R^2\text{,}\) and \(r\) for a linear model.

  1. Navigate to STAT (MENU button, then hit the 2 button or select STAT).
    🔗
    🔗
  2. Enter the \(x\) and \(y\) data into 2 separate lists, e.g. \(x\) values in List 1 and \(y\) values in List 2. Observation ordering should be the same in the two lists. For example, if \((5, 4)\) is the second observation, then the second value in the \(x\) list should be 5 and the second value in the \(y\) list should be 4.
    🔗
    🔗
  3. Navigate to CALC (F2) and then SET (F6) to set the regression context.
    • To change the 2Var XList, navigate to it, select List (F1), and enter the proper list number. Similarly, set 2Var YList to the proper list.
      🔗
      🔗
    🔗
    🔗
  4. Hit EXIT.
    🔗
    🔗
  5. Select REG (F3), X (F1), and a+bx (F2), which returns:
    🔗
    a \(a\text{,}\) the y-intercept of the best fit line
    b \(b\text{,}\) the slope of the best fit line
    r \(r\text{,}\) the correlation coefficient
    \(r^2\) \(R^2\text{,}\) the explained variance
    MSe Mean squared error, which you can ignore
    If you select ax+b (F1), the a and b meanings will be reversed.
    🔗
    🔗
🔗
🔗

Guided Practice 8.2.20.

The data set loan50, introduced in Chapter 1, contains information on randomly sampled loans offered through Lending Club. A subset of the data matrix is shown in Table 8.2.21. Use a calculator to find the equation of the least squares regression line for predicting loan amount from total income.
 14 
a\(= 6497\) and b\(= 0.0774\text{,}\) therefore \(\hat{y}=6497+0.0774x\)
🔗
Table 8.2.21. Sample of data from loan50.
🔗
total_income loan_amount
1 59000 22000
2 60000 6000
3 75000 25000
4 75000 6000
5 254000 25000
6 67000 6400
7 28800 3000
🔗
🔗

Subsection 8.2.7 Types of outliers in linear regression

Outliers in regression are observations that fall far from the “cloud” of points. These points are especially important because they can have a strong influence on the least squares line.
🔗

Example 8.2.22.

There are six plots shown in Figure 8.2.23 along with the least squares line and residual plots. For each scatterplot and residual plot pair, identify any obvious outliers and note how they influence the least squares line. Recall that an outlier is any point that doesn’t appear to belong with the vast majority of the other points.
🔗
Solution.
  1. There is one outlier far from the other points, though it only appears to slightly influence the line.
    🔗
    🔗
  2. There is one outlier on the right, though it is quite close to the least squares line, which suggests it wasn’t very influential.
    🔗
    🔗
  3. There is one point far away from the cloud, and this outlier appears to pull the least squares line up on the right; examine how the line around the primary cloud doesn’t appear to fit very well.
    🔗
    🔗
  4. There is a primary cloud and then a small secondary cloud of four outliers. The secondary cloud appears to be influencing the line somewhat strongly, making the least squares line fit poorly almost everywhere. There might be an interesting explanation for the dual clouds, which is something that could be investigated.
    🔗
    🔗
  5. There is no obvious trend in the main cloud of points and the outlier on the right appears to largely control the slope of the least squares line.
    🔗
    🔗
  6. There is one outlier far from the cloud, however, it falls quite close to the least squares line and does not appear to be very influential.
    🔗
    🔗
🔗
🔗
🔗
Figure 8.2.23. Six plots, each with a least squares line and residual plot. All data sets have at least one outlier.
🔗
Examine the residual plots in Figure 8.2.23. You will probably find that there is some trend in the main clouds of (3) and (4). In these cases, the outliers influenced the slope of the least squares lines. In (5), data with no clear trend were assigned a line with a large trend simply due to one outlier (!).
🔗

Leverage.

Points that fall horizontally away from the center of the cloud tend to pull harder on the line, so we call them points with high leverage.
🔗
🔗
Points that fall horizontally far from the line are points of high leverage; these points can strongly influence the slope of the least squares line. If one of these high leverage points does appear to actually invoke its influence on the slope of the line — as in cases (3), (4), and (5) of Example 8.2.22 — then we call it an influential point. Usually we can say a point is influential if, had we fitted the line without it, the influential point would have been unusually far from the least squares line.
🔗
It is tempting to remove outliers. Don’t do this without a very good reason. Models that ignore exceptional (and interesting) cases often perform poorly. For instance, if a financial firm ignored the largest market swings — the “outliers” — they would soon go bankrupt by making poorly thought-out investments.
🔗

Don’t ignore outliers when fitting a final model.

If there are outliers in the data, they should not be removed or ignored without a good reason. Whatever final model is fit to the data would not be very helpful if it ignores the most exceptional cases.
🔗
🔗
🔗

Subsection 8.2.8 Categorical predictors with two levels (special topic)

Categorical variables are also useful in predicting outcomes. Here we consider a categorical predictor with two levels (recall that a level is the same as a category). We’ll consider eBay auctions for a video game, Mario Kart for the Nintendo Wii, where both the total price of the auction and the condition of the game were recorded.
 15 
These data were collected in Fall 2009 and may be found at openintro.org/stat.
Here we want to predict total price based on game condition, which takes values used and new. A plot of the auction data is shown in Figure 8.2.24.
🔗
Figure 8.2.24. Total auction prices for the game Mario Kart, divided into used (\(x=0\)) and new (\(x=1\)) condition games with the least squares regression line shown.
🔗
To incorporate the game condition variable into a regression equation, we must convert the categories into a numerical form. We will do so using an indicator variable called cond_new, which takes value 1 when the game is new and 0 when the game is used. Using this indicator variable, the linear model may be written as
\begin{gather*} \widehat{\text{price}} = \alpha + \beta \times \text{cond new} \end{gather*}
🔗
The fitted model is summarized in Table 8.2.25, and the model with its parameter estimates is given as
\begin{gather*} \widehat{\text{price}} = 42.87 + 10.90 \times \text{cond new} \end{gather*}
🔗
For categorical predictors with two levels, the linearity assumption will always be satisfied. However, we must evaluate whether the residuals in each group are approximately normal with equal variance. Based on Figure 8.2.24, both of these conditions are reasonably satisfied.
🔗
Table 8.2.25. Least squares regression summary for the Mario Kart data.
🔗
Estimate Std. Error t value Pr\((>|t|)\)
(Intercept) 42.87 0.81 52.67 0.0000
cond_new 10.90 1.26 8.66 0.0000

Example 8.2.26.

Interpret the two parameters estimated in the model for the price of Mario Kart in eBay auctions.
🔗
Solution.
The intercept is the estimated price when cond_new takes value 0, i.e. when the game is in used condition. That is, the average selling price of a used version of the game is $42.87.
🔗
The slope indicates that, on average, new games sell for about $10.90 more than used games.
🔗
🔗
🔗

Interpreting model estimates for categorical predictors..

The estimated intercept is the value of the response variable for the first category (i.e. the category corresponding to an indicator value of 0). The estimated slope is the average change in the response variable between the two categories.
🔗
🔗
🔗

Subsection 8.2.9 Section summary

  • We define the best fit line as the line that minimizes the sum of the squared residuals (errors) about the line. That is, we find the line that minimizes \((y_1 - \hat{y}_1)^2 + (y_2-\hat{y}_2)^2+ \dots + (y_n-\hat{y}_n)^2=\sum{(y_i - \hat{y}_i)^2}\text{.}\) We call this line the least squares regression line.
    🔗
    🔗
  • We write the least squares regression line in the form: \(\hat{y} = a + bx\text{,}\) and we can calculate \(a\) and \(b\) based on the summary statistics as follows:
    \begin{gather*} b=r\frac{s_y}{s_x} \qquad \text{ and } \qquad a=\bar{y} - b\bar{x}\text{.} \end{gather*}
    🔗
    🔗
  • Interpreting the slope and y-intercept of a linear model
    • The slope, \(b\text{,}\) describes the average increase or decrease in the \(y\) variable if the explanatory variable \(x\) is one unit larger.
      🔗
      🔗
    • The y-intercept, \(a\text{,}\) describes the average or predicted outcome of \(y\) if \(x=0\text{.}\) The linear model must be valid all the way to \(x=0\) for this to make sense, which in many applications is not the case.
      🔗
      🔗
    🔗
    🔗
  • Two important considerations about the regression line
    • The regression line provides estimates or predictions, not actual values. It is important to know how large \(s\text{,}\) the standard deviation of the residuals, is in order to know about how much error to expect in these predictions.
      🔗
      🔗
    • The regression line estimates are only reasonable within the domain of the data. Predicting \(y\) for \(x\) values that are outside the domain, known as extrapolation, is unreliable and may produce ridiculous results.
      🔗
      🔗
    🔗
    🔗
  • Using \(R^2\) to assess the fit of the model
    • \(R^2\text{,}\) called R-squared or the explained variance, is a measure of how well the model explains or fits the data. \(R^2\) is always between 0 and 1, inclusive, or between 0% and 100%, inclusive. The higher the value of \(R^2\text{,}\) the better the model “fits” the data.
      🔗
      🔗
    • The \(R^2\) for a linear model describes the proportion of variation in the \(y\) variable that is explained by the regression line.
      🔗
      🔗
    • \(R^2\) applies to any type of model, not just a linear model, and can be used to compare the fit among various models.
      🔗
      🔗
    • The correlation \(r = - \sqrt{R^2}\) or \(r = \sqrt{R^2}\text{.}\) The value of \(R^2\) is always positive and cannot tell us the direction of the association. If finding \(r\) based on \(R^2\text{,}\) make sure to use either the scatterplot or the slope of the regression line to determine the sign of \(r\text{.}\)
      🔗
      🔗
    🔗
    🔗
  • When a residual plot of the data appears as a random cloud of points, a linear model is generally appropriate. If a residual plot of the data has any type of pattern or curvature, such as a \(\cup\)-shape, a linear model is not appropriate.
    🔗
    🔗
  • Outliers in regression are observations that fall far from the “cloud” of points.
    🔗
    🔗
  • An influential point is a point that has a big effect or pull on the slope of the regression line. Points that are outliers in the \(x\) direction will have more pull on the slope of the regression line and are more likely to be influential points.
    🔗
    🔗
🔗
🔗

Exercises 8.2.10 Exercises

1. Units of regression.

Consider a regression predicting weight (kg) from height (cm) for a sample of adult males. What are the units of the correlation coefficient, the intercept, and the slope?
🔗
Solution.
Correlation: no units. Intercept: kg. Slope: kg/cm.
🔗
🔗
🔗

2. Which is higher?

Determine if I or II is higher or if they are equal. Explain your reasoning. For a regression line, the uncertainty associated with the slope estimate, \(b_1\text{,}\) is higher when
  1. there is a lot of scatter around the regression line or
    🔗
    🔗
  2. there is very little scatter around the regression line
    🔗
    🔗
🔗
🔗

3. Over-under, Part I.

Suppose we fit a regression line to predict the shelf life of an apple based on its weight. For a particular apple, we predict the shelf life to be 4.6 days. The apple’s residual is -0.6 days. Did we over or under estimate the shelf-life of the apple? Explain your reasoning.
🔗
Solution.
Over-estimate. Since the residual is calculated as \(observed - predicted\text{,}\) a negative residual means that the predicted value is higher than the observed value.
🔗
🔗
🔗

4. Over-under, Part II.

Suppose we fit a regression line to predict the number of incidents of skin cancer per 1,000 people from the number of sunny days in a year. For a particular year, we predict the incidence of skin cancer to be 1.5 per 1,000 people, and the residual for this year is 0.5. Did we over or under estimate the incidence of skin cancer? Explain your reasoning.
🔗
🔗

5. Tourism spending.

The Association of Turkish Travel Agencies reports the number of foreign tourists visiting Turkey and tourist spending by year.
 16 
Association of Turkish Travel Agencies, Foreign Visitors Figure & Tourist Spendings By Years.
Three plots are provided: scatterplot showing the relationship between these two variables along with the least squares fit, residuals plot, and histogram of residuals.
🔗
  1. Describe the relationship between number of tourists and spending.
    🔗
    🔗
  2. What are the explanatory and response variables?
    🔗
    🔗
  3. Why might we want to fit a regression line to these data?
    🔗
    🔗
  4. Do the data meet the conditions required for fitting a least squares line? In addition to the scatterplot, use the residual plot and histogram to answer this question.
    🔗
    🔗
🔗
Solution.
  1. There is a positive, very strong, linear association between the number of tourists and spending.
    🔗
    🔗
  2. Explanatory: number of tourists (in thousands). Response: spending (in millions of US dollars).
    🔗
    🔗
  3. We can predict spending for a given number of tourists using a regression line. This may be useful information for determining how much the country may want to spend in advertising abroad, or to forecast expected revenues from tourism.
    🔗
    🔗
  4. Even though the relationship appears linear in the scatterplot, the residual plot actually shows a nonlinear relationship. This is not a contradiction: residual plots can show divergences from linearity that can be difficult to see in a scatterplot. A simple linear model is inadequate for modeling these data. It is also important to consider that these data are observed sequentially, which means there may be a hidden structure not evident in the current plots but that is important to consider.
    🔗
    🔗
🔗
🔗
🔗

6. Nutrition at Starbucks, Part I.

The scatterplot below shows the relationship between the number of calories and amount of carbohydrates (in grams) Starbucks food menu items contain.
 17 
Source: Starbucks.com, collected on March 10, 2011, www.starbucks.com/menu/nutrition.
Since Starbucks only lists the number of calories on the display items, we are interested in predicting the amount of carbs a menu item has based on its calorie content.
🔗
  1. Describe the relationship between number of calories and amount of carbohydrates (in grams) that Starbucks food menu items contain.
    🔗
    🔗
  2. In this scenario, what are the explanatory and response variables?
    🔗
    🔗
  3. Why might we want to fit a regression line to these data?
    🔗
    🔗
  4. Do these data meet the conditions required for fitting a least squares line?
    🔗
    🔗
🔗
🔗

7. The Coast Starlight, Part II.

Exercise 8.1.6.11 introduces data on the Coast Starlight Amtrak train that runs from Seattle to Los Angeles. The mean travel time from one stop to the next on the Coast Starlight is 129 mins, with a standard deviation of 113 minutes. The mean distance traveled from one stop to the next is 108 miles with a standard deviation of 99 miles. The correlation between travel time and distance is 0.636.
  1. Write the equation of the regression line for predicting travel time.
    🔗
    🔗
  2. Interpret the slope and the intercept in this context.
    🔗
    🔗
  3. Calculate \(R^2\) of the regression line for predicting travel time from distance traveled for the Coast Starlight, and interpret \(R^2\) in the context of the application.
    🔗
    🔗
  4. The distance between Santa Barbara and Los Angeles is 103 miles. Use the model to estimate the time it takes for the Starlight to travel between these two cities.
    🔗
    🔗
  5. It actually takes the Coast Starlight about 168 mins to travel from Santa Barbara to Los Angeles. Calculate the residual and explain the meaning of this residual value.
    🔗
    🔗
  6. Suppose Amtrak is considering adding a stop to the Coast Starlight 500 miles away from Los Angeles. Would it be appropriate to use this linear model to predict the travel time from Los Angeles to this point?
    🔗
    🔗
🔗
Solution.
  1. First calculate the slope: \(b_{1} = r \times s_{y} / s_{x} = 0.636 \times 113/99 = 0.726\text{.}\) Next, make use of the fact that the regression line passes through the point \((\bar{x}, \bar{y}): \bar{y} = a + b \times \bar{x}\text{.}\) Plug in \(\bar{x}\text{,}\) \(\bar{y}\) and \(b\text{,}\) and solve for \(a: 51\text{.}\) Solution: \(\widehat{\text{travel time}} = 51 + 0.726 \times \text {distance}\text{.}\)
    🔗
    🔗
  2. \(b:\) For each additional mile in distance, the model predicts an additional 0.726 minutes in travel time. \(a:\) When the distance traveled is 0 miles, the travel time is expected to be 51 minutes. It does not make sense to have a travel distance of 0 miles in this context. Here, the y-intercept serves only to adjust the height of the line and is meaningless by itself.
    🔗
    🔗
  3. \(R^2 = 0.6362^2 = 0.40\text{.}\) About 40% of the variability in travel time is accounted for by the model, i.e. explained by the distance traveled.
    🔗
    🔗
  4. \(\widehat{\text{travel time}} = 51 + 0.726 \times \text {distance} = 51 + 0.726 \times 103 \approx 126\) minutes. (Note: we should be cautious in our predictions with this model since we have not yet evaluated whether it is a well-fit model.)
    🔗
    🔗
  5. \(e_{i} = y_{i} -\hat{y}_{i} = 168 - 126 = 42\) minutes. A positive residual means that the model underestimates the travel time.
    🔗
    🔗
  6. No, this calculation would require extrapolation.
    🔗
    🔗
🔗
🔗
🔗

8. Body measurements, Part III.

Exercise 8.1.6.13 introduces data on shoulder girth and height of a group of individuals. The mean shoulder girth is 107.20 cm with a standard deviation of 10.37 cm. The mean height is 171.14 cm with a standard deviation of 9.41 cm. The correlation between height and shoulder girth is 0.67.
  1. Write the equation of the regression line for predicting height.
    🔗
    🔗
  2. Interpret the slope and the intercept in this context.
    🔗
    🔗
  3. Calculate \(R^2\) of the regression line for predicting height from shoulder girth, and interpret it in the context of the application.
    🔗
    🔗
  4. A randomly selected student from your class has a shoulder girth of 100 cm. Predict the height of this student using the model.
    🔗
    🔗
  5. The student from part (d) is 160 cm tall. Calculate the residual, and explain what this residual means.
    🔗
    🔗
  6. A one year old has a shoulder girth of 56 cm. Would it be appropriate to use this linear model to predict the height of this child?
    🔗
    🔗
🔗
🔗

9. Murders and poverty, Part I.

The following regression output is for predicting annual murders per million from percentage living in poverty in a random sample of 20 metropolitan areas.
🔗
Estimate Std. Error t value Pr\((\gt|t|)\)
(Intercept) -29.901 7.789 -3.839 0.001
poverty% 2.559 0.390 6.562 0.000
\(s = 5.512\) \(R^2 = 70.52\%\) \(R^2_{adj} = 68.89\%\)
  1. Write out the linear model.
    🔗
    🔗
  2. Interpret the intercept.
    🔗
    🔗
  3. Interpret the slope.
    🔗
    🔗
  4. Interpret \(R^2\text{.}\)
    🔗
    🔗
  5. Calculate the correlation coefficient.
    🔗
    🔗
🔗
Solution.
  1. \(\widehat{murder} = -29.901 + 2.559 \times \text{poverty}\%\text{.}\)
    🔗
    🔗
  2. Expected murder rate in metropolitan areas with no poverty is \(-29.901\) per million. This is obviously not a meaningful value, it just serves to adjust the height of the regression line.
    🔗
    🔗
  3. For each additional percentage increase in poverty, we expect murders per million to be higher on average by 2.559.
    🔗
    🔗
  4. Poverty level explains 70.52% of the variability in murder rates in metropolitan areas.
    🔗
    🔗
  5. \(\sqrt{0.7052} = 0.8398\text{.}\)
    🔗
    🔗
🔗
🔗
🔗

10. Cats, Part I.

The following regression output is for predicting the heart weight (in g) of cats from their body weight (in kg). The coefficients are estimated using a dataset of 144 domestic cats.
🔗
Estimate Std. Error t value Pr\((\gt|t|)\)
(Intercept) -0.357 0.692 -0.515 0.607
body wt 4.034 0.250 16.119 0.000
\(s = 1.452\) \(R^2 = 64.66\%\) \(R^2_{adj} = 64.41\%\)
  1. Write out the linear model.
    🔗
    🔗
  2. Interpret the intercept.
    🔗
    🔗
  3. Interpret the slope.
    🔗
    🔗
  4. Interpret \(R^2\text{.}\)
    🔗
    🔗
  5. Calculate the correlation coefficient.
    🔗
    🔗
🔗
🔗

11. Outliers, Part I.

Identify the outliers in the scatterplots shown below, and determine what type of outliers they are. Explain your reasoning.
🔗
Solution.
  1. There is an outlier in the bottom right. Since it is far from the center of the data, it is a point with high leverage. It is also an infuential point since, without that observation, the regression line would have a very different slope.
    🔗
    🔗
  2. There is an outlier in the bottom right. Since it is far from the center of the data, it is a point with high leverage. However, it does not appear to be affecting the line much, so it is not an infuential point.
    🔗
    🔗
  3. The observation is in the center of the data (in the x-axis direction), so this point does not have high leverage. This means the point won’t have much effect on the slope of the line and so is not an infuential point.
    🔗
    🔗
🔗
🔗
🔗

12. Outliers, Part II.

Identify the outliers in the scatterplots shown below and determine what type of outliers they are. Explain your reasoning.
🔗
🔗

13. Urban homeowners, Part I.

The scatterplot below shows the percent of families who own their home vs. the percent of the population living in urban areas.
 18 
United States Census Bureau, 2010 Census Urban and Rural Cassification and Urban Area Criteria and Housing Characteristics: 2010.
There are 52 observations, each corresponding to a state in the US. Puerto Rico and District of Columbia are also included.
🔗
  1. Describe the relationship between the percent of families who own their home and the percent of the population living in urban areas.
    🔗
    🔗
  2. The outlier at the bottom right corner is District of Columbia, where 100% of the population is considered urban. What type of an outlier is this observation?
    🔗
    🔗
🔗
Solution.
  1. There is a negative, moderate-to-strong, somewhat linear relationship between percent of families who own their home and the percent of the population living in urban areas in 2010. There is one outlier: a state where 100% of the population is urban. The variability in the percent of homeownership also increases as we move from left to right in the plot.
    🔗
    🔗
  2. The outlier is located in the bottom right corner, horizontally far from the center of the other points, so it is a point with high leverage. It is an infuential point since excluding this point from the analysis would greatly affect the slope of the regression line.
    🔗
    🔗
🔗
🔗
🔗

14. Crawling babies, Part II.

Exercise 8.1.6.12 introduces data on the average monthly temperature during the month babies first try to crawl (about 6 months after birth) and the average first crawling age for babies born in a given month. A scatterplot of these two variables reveals a potential outlying month when the average temperature is about 53°F and average crawling age is about 28.5 weeks. Does this point have high leverage? Is it an influential point?
🔗
🔗
🔗
You have attempted of activities on this page.
🔗
PrevTopNext