Principle 12.3.2. EFFECTIVE DESIGN: Recursive Progress.
In a recursive algorithm, each recursive call must make progress toward the bound, or base case.
println() method for printing strings. But pretend for a moment that you only have a version of println() that works for characters, and your task is to write a version that can be used to print an entire string of characters./**
* printString() prints each character of the string s
* Pre: s is initialized (non-null)
* Post: none
*/
public void printString(String s) {
if (s.length() == 0)
return; // Base case: do nothing
else { // Recursive case:
System.out.print(s.charAt(0)); // Print head
printString(s.substring(1)); // Print tail
}
} // printString()
printString() method.printString()’s internal state completely in terms of its recursion parameter, s, which is the string that’s being printed. A recursion parameter is a parameter whose value is used to control the progress of the recursion. In this case, if s differs in each copy, then so will s.substring(1) and s.charAt(0).printString("hello") is invoked.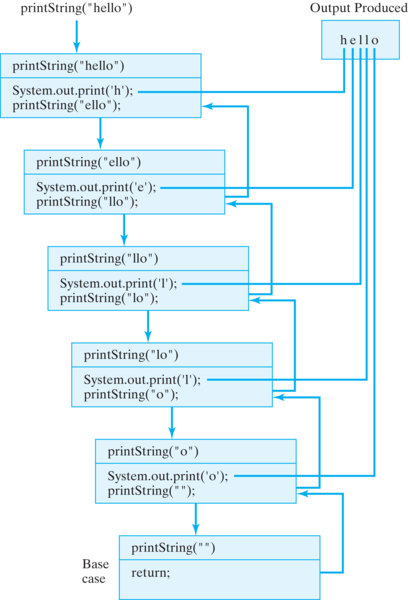
printString() method, with its own internal state. In this illustration, its state is represented by its parameter, s. Because each instance has a different parameter, behaviors differ slightly. Each box shows the character that will be printed by that instance (s.charAt(0)), and the string that will be passed on to the next instance (s.substring(1)).s.charAt(0) and s.substring(1) will generate exceptions if s is the empty string.return executed is the one in the base case. Each instance of the method must wait for the instance it called to return before it can return. That’s why the instances “pile up” in a cascade-like structure. The arrowless lines trace the order in which the output is produced.printString() is similar to the next in that each will print one character and then pass on a substring, but each performs its duties on a different string. Note how the string, the recursion parameter in this case, gets smaller in each instance of printString(). This represents progress toward the method’s base case s.length() == 0. When the empty string is passed as an argument, the recursion will stop. If the method does not make progress toward its bound in this way, the result will be an infinite recursion.s.charAt(0) is printed, and then s.substring(1) is passed to printString() in the recursion. This is a typical structure for a head-and-tail algorithm. What makes this work is that the tail is a smaller, self-similar version of the original structure.printString2() method, if it is called with printString2("hello")?
public void printString2(String s) {
if (s.length() == 1)
System.out.print(s.charAt(0)); // Base case:
else { // Recursive case
System.out.print(s.charAt(s.length() - 1));
printString2(s.substring(0, s.length() - 1));
}
} // printString2()
printString() method? That is, what if the recursive call came before s.charAt(0) is printed, as in the following method:/**
* printReverse() prints each character s in reverse order
* Pre: s is initialized (non-null)
* Post: none
*/
public void printReverse(String s) {
if (s.length() > 0) { // Recursive case:
printReverse(s.substring(1)); // Print tail
System.out.print(s.charAt(0)); // Print first char
}
} // printReverse()
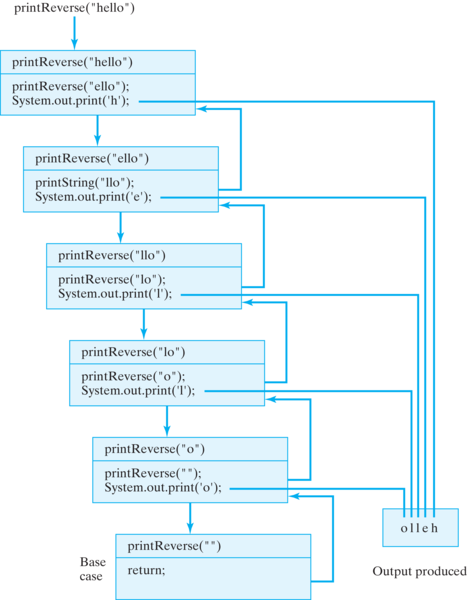
printReverse(s), which prints its string argument in reverse order.printReverse("hello") can print h, it calls printReverse("ello") and must wait for that call to complete its execution and return. But printReverse("ello") calls printReverse("llo") and so must wait for that call to complete its execution and return.printReverse("") is called. While the base case is executing, the other five instances of printReverse() must each wait for the instance that they called to complete its execution. It is only after the base case returns, that printReverse("o") can print its first character and return.printReverse("o") has returned, then printReverse("lo") can print its first character. So the letter l will be printed next, and so on, until the original call to printReverse("hello") is completed and returns. Thus, the string will be printed in reverse order.countDown() that takes a single int parameter, \(N \geq 0\text{,}\) and prints a countdown, such as “5, 4, 3, 2, 1, blastoff.” The main program is completed for you.countDown(10), it will print “10 8 6 4 2 blastoff”; if it’s called with countDown(9), it prints “9 7 5 3 1 blastoff.” The main program is completed for you.String to store the string that will be processed and a char to store the target character—the one we want to count. The method should return an int, representing the number of occurrences of the target character in the string:// Goal: count the occurrences of ch in s
public int countChar(String s, char ch) {
...
}
countChar() should just return 0 as its result./**
* Pre: s is a non-null String, ch is any character
* Post: countChar() == the number of occurrences of ch in str
*/
public int countChar(String s, char ch) {
if (s.length() == 0) // Base case: empty string
return 0;
else if (s.charAt(0) == ch) // Recursive case 1
return 1 + countChar(s.substring(1), ch); // Head = ch
else // Recursive case 2
return 0 + countChar(s.substring(1), ch); // Head != ch
} // countChar()
countChar() method.return 1 + countChar(s.substring(1),ch); // Head = ch
countChar(s.substring(1),ch) and add it to 1. Only then can a result be returned to the calling method. This leads to the following evaluation sequence for countChar("dad",'d'):countChar("dad",'d');
1 + countChar("ad",'d');
1 + 0 + countChar("d",'d');
1 + 0 + 1 + countChar("",'d');
1 + 0 + 1 + 0 = 2 // Final result
countChar("dad",'d') is built up recursively by adding together the partial results from each separate instance of countChar(). The evaluation process is shown graphically in Figure 12.3.11.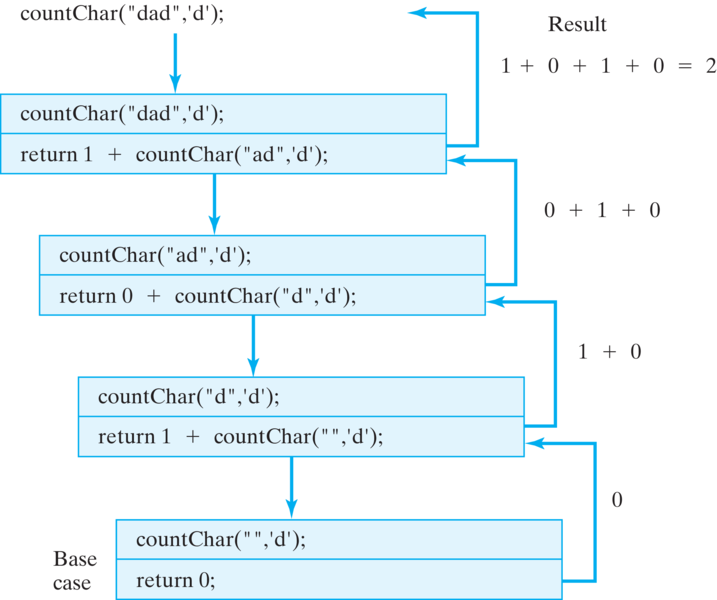
countChar("dad",'d'), which returns the value 2./unix_system/myfolder/java
\Windows_system\myfolder\java
String, on which the conversion will be performed, and two char variables, the first being the original character in the string and the second being its substitute. The precondition for this method is simply that each of these three parameters has been properly initialized with a value. The postcondition is that all occurrences of the first character have been replaced by the second character./**
* Pre: str, ch1, ch2 have been initialized
* Post: the result contains a ch2 everywhere that ch1
* had occurred in str
*/
public static String convert(String str, char ch1, char ch2) {
if (str.length() == 0) // Base case: empty string
return str;
else if (str.charAt(0) == ch1) // Recursive 1: ch1 at head
// Replace ch1 with ch2
return ch2 + convert(str.substring(1), ch1, ch2);
else // Recursive 2: ch1 not at head
return str.charAt(0) + convert(str.substring(1), ch1, ch2);
} // convert()
convert() method replaces one character with another in a string.str is the empty string. The first recursive case occurs when the character being replaced is the head of str. In that case, its substitute (ch2) is concatenated with the result of converting the rest of the string and returned as the result. The second recursive case occurs when the head of the string is not the character being replaced. In this case, the head of the string is simply concatenated with the result of converting the rest of the string. Figure 12.3.14 shows an example of its execution.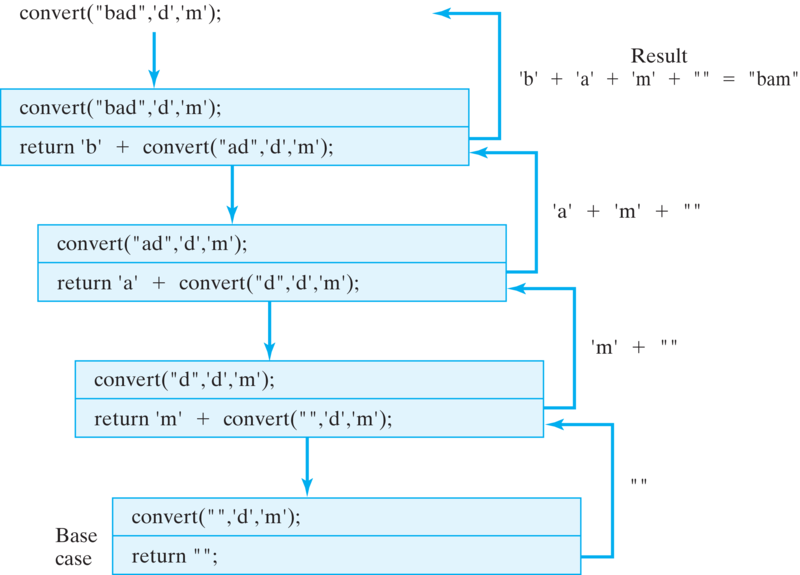
convert("bad",'d','m'), which returns “bam.”convert() method, taking care to notice the different state of the method on each recursive call. It should match Figure 12.3.14. addBlanks() that changes each blank in a string into two consecutive blanks, leaving the rest of the string unchanged.H’s and T’s corresponding to heads and tails.HT represents a head on the first coin and a tail on the second coin. What we need is a method which, when given the number of coins, will print out all strings of this type. In case of two coins the output should be:HH
HT
TH
TT
H on one line and a T on the next line.H and those that start with a T. The strings that start with H can be generated by inserting an H in front of each of the outcomes that occur when \(N-1\) coins are tossed. The strings beginning with T can be generated in a similar manner. Thus, using the outcomes for two coins above, we know that the outcomes for three coins for which the first coin is H are:HHH
HHT
HTH
HTT
STR representing one particular outcome for all but the last \(K\) coins where \(0 \lt K \lt = N\text{.}\)
STR + "H" for all but the last \(K - 1\) coins and then print all outcomes with the fixed outcome STR + "T" for all but the last \(K - 1\) coins. The base case is the special case \(K = 1\) when you just need STR
+ "H" on one line and STR + "T" on the next. If you start the algorithm with STR = "" and \(K = N\text{,}\) this algorithm will print out all the outcomes for tossing \(N\) coins.printOutcomes(String str,int N). The above recursive description easily translates into code for the method in Listing 12.3.15./**
* printOutcomes(str, N) prints out all possible outcomes
* beginning with str when N more coins are tossed.
* Pre: str is a string of Hs and Ts.
* Pre: N is a positive integer.
* Post: none
*/
public static void printOutcomes(String str,int N){
if (N == 1) { // The base case
System.out.println(str + "H");
System.out.println(str + "T");
} else { // The recursive case
printOutcomes(str + "H", N - 1);
printOutcomes(str + "T", N - 1);
} //else
}// printOutcomes()
printOutcomes() prints all outcomes given the results on some initial coins.CoinToss.printOutcomes("",7). This particular call would generate the desired output:HHHHHHH
HHHHHHT
.......
TTTTTTH
TTTTTTT
System.out that occurs when executing printOutcomes("",3) as shown in Figure 12.3.16.
printOutcomes> method, taking care to notice the different state of the method on each recursive call. Note that in this algorithm there are two recursive calls in the recursive case. It should match Figure 12.3.16.printOutcomes() method so that it will print out all possible outcomes when a chess player plays a series of \(N\) games. The outcome of each game is to be represented by a W, L, or D corresponding to the player winning, losing, or drawing the game.