Section6.5Graphics Example: Drawing a Checkerboard
In this section we will combine some of the graphics methods we have learned ith the nested for-loop structure to draw a checkerboard with checkers on it (Figure 6.5.1).
Figure6.5.1.Checkerboard For this example, we will just concentrate on drawing the checkerboard. We will not worry about providing a full checkerboard representation, of the sort we would need if we were writing a program to play the game of checkers. So, our design will not involve instance variables for whose turn it is, how many checkers each player has, where the checkers are located on the board, and other elements of the game’s state. Still, our visible representation of the board should be designed so that it will eventually be useful when we do develop a checkers game in Chapter 8.
Subsection6.5.1Problem Description and Specification
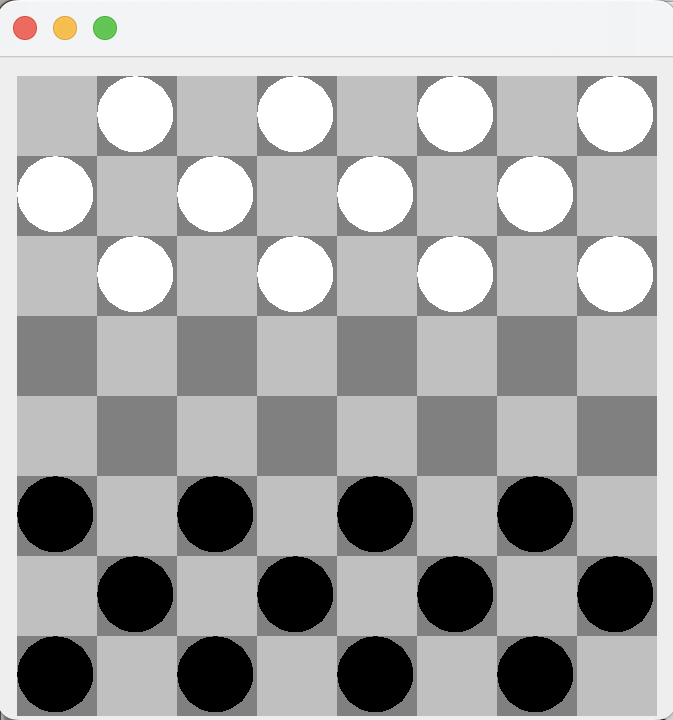
The specification for this problem is to develop a program that will draw a checkerboard and place the checkers on it in their appropriate starting positions. As with many of our programs, our design will involve two classes, one which defines the user interface and the other which represents the computational object. For this problem, the computational object will be defined in the CheckerBoard class. The details of its design are described in the next section.
Because the purpose of this example is to focus on how we use loops and drawing methods, we will employ a very simple JFrame interface, whose implementation is given in Figure 6.5.2.
import java.awt.*;
import javax.swing.*;
public class CheckerBoardFrame extends JFrame {
private CheckerBoard theBoard;
public CheckerBoardFrame() {
theBoard = new CheckerBoard();
}
public void paint(Graphics g) {
super.paint(g);
theBoard.draw(g);
} // paint()
public static void main(String[] args){
CheckerBoardFrame c = new CheckerBoardFrame();
c.setSize(500,500);
c.setVisible(true);
}
} // CheckerBoardFrame
Figure6.5.2.The CheckerBoardFrame class.
As shown there, the program simply creates a CheckerBoard instance in its CheckerBoardFrame() constructor, and then invokes the CheckerBoard’s draw method in its paint() method. The reason we invoke the draw() method in paint() is because we need to have access to the JFrame’s Graphics context, which is passed as an argument to the draw() method. Recall that the main() method is invoked when CheckerBoardFrame is run,and then the paint() methods are invoked automatically by calling the setVisible(true) method in main(). Thus, the action taken by this program is simply to draw a visual representation of the checkerboard.
Subsection6.5.2Class Design: CheckerBoard
Figure6.5.3.The CheckerBoard class The draw() method must be public and a part of the CheckerBoard’s interface. The task of drawing a checkerboard involves two distinct subtasks: (1) drawing the board itself, which will involve drawing a square with smaller squares of alternating colors; and, (2) drawing the checkers on the checkerboard. A good design for the draw() method would be simply to invoke helper methods that encapsulate these two subtasks. This is good method design because it results in relatively small methods, each of which performs a very well-defined task. Let’s call these methods drawBoard() and drawCheckers(), respectively. Their signatures are shown in Figure 6.5.3, which summarizes the design of the CheckerBoard class.
Before getting into the details of the drawBoard and drawCheckers() methods, we must first discuss CheckerBoard’s several instance variables. The first two variables LEFT_X and UPPER_Y, give the absolute position of the upper left corner of the checkerboard on the JFrame’s drawing panel. The SQ_SIDE variable gives the size of the checkerboard’s individual squares. N_ROWS and N_COLS give the number of rows and columns in the checkerboard (typically, 8 by 8). All of these variables are integers. The final four variables, SQ_COLOR1, SQ_COLOR2, CHECKER_COLOR1, and CHECKER_COLOR2, specify the colors of the checkerboard and the checkers.
Note that the names of all the instance variables are written in uppercase letters. This is to identify them as symbolic constants—that is, as final variables whose values do not chage once they are initialized. Because their actual values are not important, we do not show them in the UML diagram and we won’t discuss them here. Recall that the advantage of defining class constants, rather than sprinkling literal values throughout the program, is that they make it easy to modify the program if we decide to change the size, location, or color of the checkerboard.
Subsection6.5.3Method Design
Returning now to the design of CheckerBoard’s instance methods, the complete definition of the CheckerBoard class is given in Figure 6.5.4. Note how simple its draw() method is.
public void draw(Graphics g) { // Draw board and checkers
drawBoard(g);
drawCheckers(g);
}
As we noted earlier, in order to using Java’s drawing commands, it is necessary to have a reference to a Graphics object. This is passed to the draw() method when the draw() method is invoked in the program. Because the draw() method delegates the details of the drawing algorithm to its helper methods, drawBoard() and drawCheckers(), it has to pass them a reference to the Graphics object.
import java.awt.*;
public class CheckerBoard {
// Default values for a standard checkerboard
private final int LEFT_X = 10; // Position of left
private final int UPPER_Y = 10; // upper corner
private final int SQ_SIDE = 40; //Size of each square
private final int N_ROWS = 8; // Checkerboard rows
private final int N_COLS = 8; // Checkerboard columns
private final Color SQ_COLOR1 = Color.lightGray; //Colors
private final Color SQ_COLOR2 = Color.gray; //of squares
private final Color CHECKER_COLOR1 = Color.white; // and
private final Color CHECKER_COLOR2 = Color.black; //checkers
private void drawBoard(Graphics g) {
for(int row = 0; row < N_ROWS; row++) // For each row
for(int col = 0; col < N_COLS; col++) { // For each square
if ((row + col) % 2 == 0) // Alternate colors
g.setColor(SQ_COLOR1); // Light
else
g.setColor(SQ_COLOR2); // or dark
g.fillRect(LEFT_X+col*SQ_SIDE,
UPPER_Y+row*SQ_SIDE,SQ_SIDE,SQ_SIDE);
} //for
} //drawBoard()
private void drawCheckers(Graphics g) { // Place checkers
for(int row = 0; row < N_ROWS; row++) // For each row
for(int col = 0; col < N_COLS; col++)// For each square
if ((row + col)%2 == 1) {// One player has top 3 rows
if (row < 3) {
g.setColor(CHECKER_COLOR1);
g.fillOval(LEFT_X+col*SQ_SIDE,
UPPER_Y+row*SQ_SIDE,SQ_SIDE-2,SQ_SIDE-2);
}//if
if (row >= N_ROWS - 3) { // Other has bottom 3 rows
g.setColor(CHECKER_COLOR2);
g.fillOval(LEFT_X+col*SQ_SIDE,
UPPER_Y+row*SQ_SIDE,SQ_SIDE-2,SQ_SIDE-2);
}//if
}//if
}//drawCheckers()
public void draw(Graphics g) { // Draw board and checkers
drawBoard(g);
drawCheckers(g);
}//draw()
} //CheckerBoard
Figure6.5.4.The CheckerBoard class.
The drawBoard() method uses a nested for loop to draw an \(8 \times 8\) array of rectangles of alternating colors. The loop variables, row and col, both range from 0 to 7. The expression used to determine alternating colors tests whether the sum of the row and column subscripts is even: \(((row + col) \% 2 == 0)\text{.}\) If their sum is even, we use one color; if odd, we use the other color.
As the table below shows for a \(4 \times 4\) board, the sum of a board’s row and column subscripts alternates between even and odd values. Thus, in row 2 column 3, the sum of the subscripts is 5.
To switch from one color to the other, we use the GraphicssetColor() method to alternate between the two colors designated for the checkerboard, SQ_COLOR1 and SQ_COLOR2. We then use the following method call to draw the colored squares:
Note how we use the loop variables, rowcol, together with the constants specifying the top left corner of the board (UPPER_Y and LEFT_X) and the size of the squares (SQ_SIDE) to calculate the location and size of each square. The calculation here is illustrated in Figure 6.5.5. The first two parameters in fillRect(left,top,width,height) specify the coordinates for the rectangle’s top-left corner. These are calculated as a function of the rectangle’s row and column position within the checkerboard and the rectangle’s width and height, which are equal for the squares of a checkerboard.
Figure6.5.5.Calculating the locations of the checkerboard squares.
The drawCheckers() method also uses a nested for loop to trace through the checkerboard’s rows and columns. In this case, however, we draw checkers on just the dark-colored squares—that is, those that satisfy the expression \((row+col) \% 2 == 1)\)—on the first three rows of each player’s side of the board. So, each player’s checkers initially are located in the first three rows and last three rows of the checker board:
if ((row + col)%2 == 1) {// One player has top 3 rows
if (row < 3){
g.setColor(CHECKER_COLOR1);
g.fillOval(LEFT_X+col*SQ_SIDE,
UPPER_Y+row*SQ_SIDE,SQ_SIDE-2,SQ_SIDE-2);
}//if
if (row >= N_ROWS - 3) { // Other has bottom 3 rows
g.setColor(CHECKER_COLOR2);
g.fillOval(LEFT_X+col*SQ_SIDE,
UPPER_Y+row*SQ_SIDE,SQ_SIDE-2,SQ_SIDE-2);
}//if
}//if
Because the checkers are circles, we use the fillOval() method to draw them. Note that the parameters for fillOval(left, top, width, height) are identical to those for fillRect(). The parameters specify an enclosing rectangle in which the oval is inscribed. In this case, of course, the enclosing rectangle is a square, which causes fillOval() to draw a circle.
Our design of the CheckerBoard class illustrates an important principle of method design. First, rather than placing all of the commands for drawing the checkerboard and the checkers into one method, we broke up this larger task into distinct subtasks. This resulted in small methods, each of which has a well defined purpose.
Methods should be designed to have a clear focus. If you find a method becoming too long, you should break its algorithm into subtasks and define a separate method for each subtask.
