Section 1.9 Exercises
-
Fill in the blanks in each of the following statements.
- A Java class definition contains an object’s
__________and__________. - A method definition contains two parts, a
__________and a__________.
- Explain the difference between each of the following pairs of concepts.
- Single-line and multiline comment.
- Compiling and running a program.
- Source code file and bytecode file.
- Syntax and semantics.
- Syntax error and semantic error.
- Data and methods.
- Variable and method.
- Algorithm and method.
- Pseudocode and Java code.
- Method definition and method invocation.
- For each of the following, identify it as either a syntax error or a semantic error. Justify your answers.
- Write a class header as
public Class MyClass. - Define the
init()header aspublic vid init(). - Print a string of five asterisks by
System.out.println("***");. - Forget the semicolon at the end of a
println()statement. - Calculate the sum of two numbers as
N - M.
- Suppose you have a Java program stored in a file named
Test.java. Describe the compilation and execution process for this program, naming any other files that would be created. - Suppose N is 15. What numbers would be output by the following pseudocode algorithm? Suppose N is 6. What would be output by the algorithm in that case?
0. Print N. 1. If N equals 1, stop. 2. If N is even, divide it by 2. 3. If N is odd, triple it and add 1. 4. Go to step 0. -
Suppose N is 5 and M is 3. What value would be reported by the following pseudocode algorithm? In general, what quantity does this algorithm calculate?
0. Write 0 on a piece of paper. 1. If M equals 0, report what's on the paper and stop. 2. Add N to the quantity written on the paper. 3. Subtract 1 from M. 4. Go to step 1. - Puzzle Problem: You are given two different length ropes that have the characteristic that they both take exactly one hour to burn. However, neither rope burns at a constant rate. Some sections of the ropes burn very fast; other sections burn very slowly. All you have to work with is a box of matches and the two ropes. Describe an algorithm that uses the ropes and the matches to calculate when exactly 45 minutes have elapsed.
- Puzzle Problem: A polar bear that lives right at the North Pole can walk due south for one hour, due east for one hour, and due north for one hour, and end up right back where it started. Is it possible to do this anywhere else on earth? Explain.
- Puzzle Problem: Lewis Carroll, the author of Alice in Wonderland, used the following puzzle to entertain his guests: A captive queen weighing 195 pounds, her son weighing 90 pounds, and her daughter weighing 165 pounds, were trapped in a very high tower. Outside their window was a pulley and rope with a basket fastened on each end. They managed to escape by using the baskets and a 75-pound weight they found in the tower. How did they do it? The problem is that anytime the difference in weight between the two baskets is more than 15 pounds, someone might get hurt. Describe an algorithm that gets them down safely.
- Puzzle Problem: Here’s another Carroll favorite: A farmer needs to cross a river with his fox, goose, and a bag of corn. There’s a rowboat that will hold the farmer and one other passenger. The problem is that the fox will eat the goose if they are left alone on the river bank, and the goose will eat the corn if they are left alone on the river bank. Write an algorithm that describes how he got across without losing any of his possessions.
- Puzzle Problem: Have you heard this one? A farmer lent the mechanic next door a 40-pound weight. Unfortunately, the mechanic dropped the weight and it broke into four pieces. The good news is that, according to the mechanic, it is still possible to use the four pieces to weigh any quantity between one 40 pounds on a balance scale. How much did each of the four pieces weigh? (Hint: You can weigh a 4-pound object on a balance by putting a 5-pound weight on one side and a 1-pound weight on the other.)
- Suppose your little sister asks you to show her how to use a pocket calculator so that she can calculate her homework average in her science course. Describe an algorithm that she can use to find the average of 10 homework grades.
- A Caesar cipher is a secret code in which each letter of the alphabet is shifted by N letters to the right, with the letters at the end of the alphabet wrapping around to the beginning. For example, if N is 1, when we shift each letter to the right, the word daze would be written as ebaf. Note that the z has wrapped around to the beginning of the alphabet. Describe an algorithm that can be used to create a Caesar encoded message with a shift of 5.
- Suppose you received the message, “sxccohv duh ixq,” which you know to be a Caesar cipher. Figure out what it says and then describe an algorithm that will always find what the message said regardless of the size of the shift that was used.
- Suppose you’re talking to your little brother on the phone and he wants you to calculate his homework average. All you have to work with is a piece of chalk and a very small chalkboard—big enough to write one four-digit number. What’s more, although your little brother knows how to read numbers, he doesn’t know how to count very well so he can’t tell you how many grades there are. All he can do is read the numbers to you. Describe an algorithm that will calculate the correct average under these conditions.
- Write a header for a public applet named
SampleApplet. - Write a header for a public method named
getName. - Design a class to represent a geometric rectangle with a given length and width, such that it is capable of calculating the area and the perimeter of the rectangle.
- Modify the
OldMacDonaldclass to “sing” either “Mary Had a Little Lamb” or your favorite nursery rhyme. - Define a Java class, called
Patterns, modeled afterOldMacDonald, that will print the following patterns of asterisks, one after the other heading down the page:***** ***** ***** **** * * * * * *** * * * * ** * * * * * * ***** ***** -
Write a Java class that prints your initials as block letters, as shown here:
****** * * * * ** ** * * * * * * ****** * * * * ** * * * * * * * * * * * * * * * - Challenge: Define a class that represents a
Temperatureobject. It should store the current temperature in an instance variable of typedouble, and it should have twopublicmethods,setTemp(double t), which assignstto the instance variable, andgetTemp(), whichreturns the value of the instance variable. Use theRiddleclass as a model. - Challenge: Define a class named
TaxWhizthat computes the sales tax for a purchase. It should store the current tax rate as an instance variable. Following the model of theRiddleclass, you can initialize the rate using aTaxWhiz()constructor. This class should have onepublicmethod,calcTax(double purchase), which willreturnadouble, whose value ispurchasestimes the tax rate. For example, if the tax rate is 4 percent, 0.04, and the purchase is $100, thencalcTax()should return 4.0. - What is stored in the variables
num1andnum2after the following statements are executed?int num1 = 5; int num2 = 8; num1 = num1 + num2; num2 = nmm1 + num2; - Write a series of statements that will declare a variable of type
intcallednumand store in it the difference between 61 and 51. - Modify the UML diagram of the
Riddleclass to contain a method namedgetRiddle()that would return both the riddle’s question and answer. - Draw a UML class diagram representing the following class: The name of the class is
Circle. It has one attribute, aradiusthat is represented by adoublevalue. It has one operation,calculateArea(), which returns adouble. Its attributes should be designated as private and its method as public. - To represent a triangle we need attributes for each of its three sides and operations to create a triangle, calculate its area, and calculate its perimeter. Draw a UML diagram to represent this triangle.
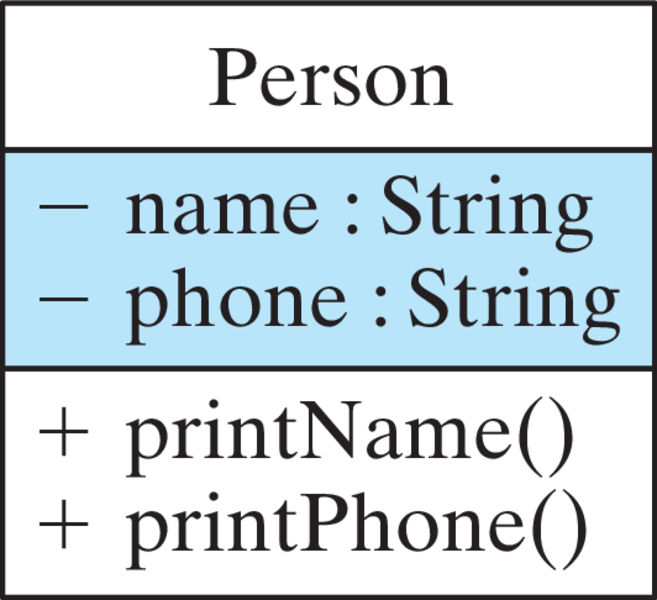
- Try to give the Java class definition for the class described in UML diagram shown here.
You have attempted of activities on this page.

