Skip to main content
Logo image

Java, Java, Java: Object-Oriented Problem Solving, 2022E

Ralph Morelli, Ralph Walde, Beryl Hoffman

Section 5.7 Numeric Processing Examples

In this section we consider several numeric programming examples. They are carefully chosen to illustrate different issues and concepts associated with processing numeric data.

Subsection 5.7.1 Example: Rounding to Two Decimal Places

As an example of how to use Math class methods, let’s consider the problem of rounding numbers. When dealing with applications that involve monetary values—dollars and cents—it is often necessary to round a calculated result to two decimal places.
For example, suppose a program computes the value of a certificate of deposit (CD) to be 75.19999. Before we output this result, we would want to round it to two decimal places—to 75.20. The following algorithm can be used to accomplish this:
Step 3 of this algorithm can be done using the Math.floor(R) method, which rounds its real argument, R, to the largest integer not less than R (from Table 5.6.1). If the number to be rounded is stored in the double variable R, then the following expression will round R to two decimal places:
R = Math.floor(R * 100.0 + 0.5) / 100.0;
Alternatively, we could use the Math.round() method ( Table 5.6.1). This method rounds a floating-point value to the nearest integer. For example, Math.round(65.3333) rounds to 65 and Math.round(65.6666) rounds to 66. The following expression uses it to round to two decimal places:
R = Math.round(100.0 * R) / 100.0;
Note that it is important here to divide by \(100.0\) and not by \(100\text{.}\) Otherwise, the division will give an integer result and we’ll lose the decimal places.

Activity 5.7.1.

Try the following demo of these math operations to round a decimal value. Try changing the value of r and try again.

Subsection 5.7.2 Example: Converting Fahrenheit to Celsius

To illustrate some of the issues that arise in using numeric data, let’s design a program that performs temperature conversions from Fahrenheit to Celsius and vice versa.

Problem Decomposition.

This problem requires two classes, a Temperature class and a TemperatureUI class. The Temperature class will perform the temperature conversions, and TemperatureUI will serve as the user interface (Figure 5.7.3).
Figure 5.7.3. Interacting objects: The user interacts with the user interface (TemperatureUI), which interacts with the Temperature object.

Class Design: Temperature.

The purpose of the Temperature class is to perform the temperature conversions. To convert a Celsius temperature to Fahrenheit or vice versa, it is not necessary to store the temperature value. Rather, a conversion method could take the Celsius (or Fahrenheit) temperature as a parameter, perform the conversion, and return the result. Therefore, the Temperature class does not need any instance variables.
Note that in this respect the Temperature class resembles the Math class. Unlike OneRowNim, which stores the game’s state — the number of sticks remaining and whose turn it is — the Math and Temperature classes are stateless. They just perform certain calculations for us.
Thus, following the design of the Math class, the Temperature class will have two public static methods: one to convert from Fahrenheit to Celsius and one to convert from Celsius to Fahrenheit. Recall that static methods are associated with the class rather than with its instances. Therefore, we needn’t instantiate a Temperature object to use these methods. Instead, we can invoke the methods through the class itself.
The methods will use the standard conversion formulas: \(F = \frac{9}{5}C + 32\) and \(C = \frac{5}{9}(F - 32)\text{.}\) Each of these methods should have a single parameter to store the temperature value that is being converted.
Because we want to be able to handle temperatures such as 98.6, we should use real-number data for the methods’ parameters. Generally speaking, because Java represents real literals such as 98.6 as double, the double type is more widely used than float. Moreover, using double wherever a floating point value is needed will cut down on the number of implicit data conversions that a program would have to perform. Therefore, each of our conversion methods should take a double parameter and return a double result.
These considerations lead to the design shown in Figure 5.7.5.
Figure 5.7.5. The Temperature class.

Implementation: Temperature.

The implementation of the Temperature class is shown in Figure 5.7.6.
public class Temperature
{
    public static double fahrToCels(double temp)
    {
        return (5.0 * (temp - 32.0) / 9.0);
    }
    public static double celsToFahr(double temp)
    {
        return (9.0 * temp / 5.0 + 32.0);
    }
} // Temperature
Figure 5.7.6. The Temperature class.
Note that because celsToFahr() uses the double value temp in its calculation, it uses floating-point literals (9.0, 5.0, and 32.0) in its conversion expression. This helps to reduce the reliance on Java’s built-in promotion rules, which can lead to subtle errors. For example, suppose we had written the celsToFahr() method using this calculation:
return (9 / 5 * temp + 32);    // Error: equals (temp + 32)
Because 9 divided by 5 gives the integer result 1, this expression is always equivalent to temp + 32, which is not the correct conversion formula. This kind of subtle semantic error can be avoided if you avoid mixing types wherever possible.

Testing and Debugging.

The next question to be addressed is how should this program be tested? As always, you should test the program in a stepwise fashion. As each method is coded, you should test it both in isolation and in combination with the other methods, if possible.
Also, you should develop appropriate test data. It is not enough to just plug in any values. The values you use should test for certain potential problems. For this program, the following tests are appropriate:
  • Test converting 0 degrees C to 32 degrees F.
  • Test converting 100 degrees C to 212 degrees F.
  • Test converting 212 degrees F to 100 degrees C.
  • Test converting 32 degrees F to 0 degrees C.
The first two tests use the celsToFahr() method to test the freezing point and boiling point temperatures, two boundary values for this problem. A boundary value is a value at the beginning or end of the range of values that a variable or calculation is meant to represent. The second pair of tests performs similar checks with the fahrToCels() method. One advantage of using these particular values is that we know what results the methods should return.

Activity 5.7.2.

Try the following demo of the Temperature converter. Try each of the tests mentioned above.

The TemperatureUI Class.

The purpose of the TemperatureUI class is to serve as a user interface—that is, as an interface between the user and a Temperature object. It will accept a Fahrenheit or Celsius temperature from the user, pass it to one of the public methods of the Temperature object for conversion, and display the result that is returned.
As we discussed in Chapter 4, the user interface can take various forms, ranging from a command-line interface to a graphical interface. Figure 5.7.10 shows a design for the user interface based on the command-line interface developed in Chapter 4. The TemperatureUI uses a KeyboardReader to handle interaction with the user and uses static methods in the Temperature class to perform the temperature conversions.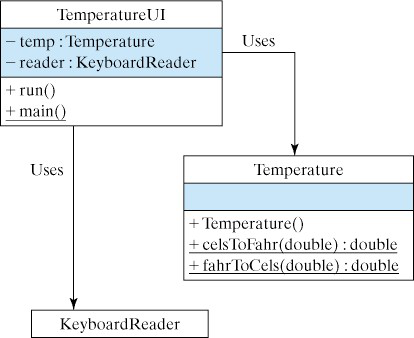
Figure 5.7.10. A command-line user interface.

Exercises Self-Study Exercises

1. TemperatureUI.
Using a development environment that allows user input and following the design in Figure 5.7.10, implement the TemperatureUI class and use it to test the methods in Temperature class. The run() method should use an input-process-output algorithm: Prompt the user for input, perform the necessary processing, and output the result.
Remember, because Temperature’s conversion methods are class methods, you do not need to instantiate a Temperature object in this project. You can invoke the conversion methods directly through the Temperature class:
double fahr = Temperature.celsToFahr(98.6);
2. Temperature GUI.
Using a development environment that allows GUI development, and following the design for the GUI developed in Chapter 4, implement a GUI to use for testing the Temperature class. The GUI should have the layout shown in Figure 5.7.11.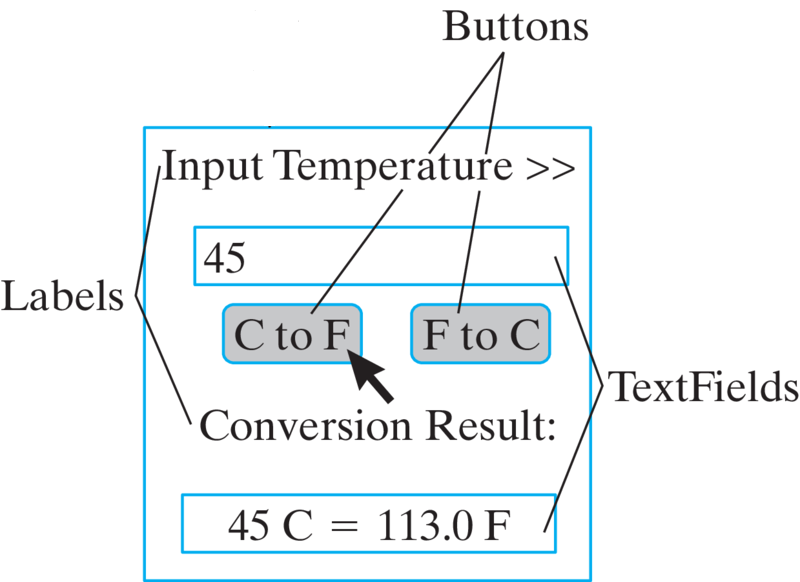
Figure 5.7.11. Temperature GUI.

Subsection 5.7.3 Example: Using Class Constants

In addition to instance variables, which are associated with instances (objects) of a class, Java also allows class variables, which are associated with the class itself. One of the most common uses of such variables is to define named constants to replace literal values. A named constant is a variable that cannot be changed once it has been given an initial value. In this section, we use our running example, OneRowNim, to illustrate using class constants.
Methods and variables that are associated with a class are declared with the static modifier. If a variable is declared static, there is exactly one copy of that variable created no matter how many times its class is instantiated. To turn a variable into a constant, it must be declared with the final modifier. Thus, the following would be examples of a class constants, constant values that are associated with the class rather than with its instances:
public static final int PLAYER_ONE = 1;
public static final int PLAYER_TWO = 2;
public static final int MAX_PICKUP = 3;
public static final int MAX_STICKS = 7;
The final modifier indicates that the value of a variable cannot be changed. When final is used in a variable declaration, the variable must be assigned an initial value. After a final variable is properly declared, it is a syntax error to attempt to try to change its value. For example, given the preceding declarations, the following assignment statement would cause a compiler error:
PLAYER_ONE = 5;  // Syntax error; PLAYER_ONE is a constant
Note how we use uppercase letters and underscore characters (_) in the names of constants. This is a convention that professional Java programmers follow, and its purpose is to make it easy to distinguish the constants from the variables in a program. This makes the program easier to read and understand.
Another way that named constants improve the readability of a program is by replacing the reliance on literal values. For example, for the OneRowNim class, compare the following two if conditions:
if (num < 1 || num > 3 || num > nSticks) ...
if (num < 1 || num > MAX_PICKUP || num > nSticks) ...
Clearly, the second condition is easier to read and understand. In the first condition, we have no good idea what the literal value 3 represents. In the second, we know that MAX_PICKUP represents the most sticks a player can pick up.
Thus, to make OneRowNim more readable, we should replace all occurrences of the literal value 3 with the constant MAX_PICKUP. This same principle would apply to some of the other literal values in the program. Thus, instead of using 1 and 2 to represent the two players, we could use PLAYER_ONE and PLAYER_TWO to make methods such as the following easier to read and understand:
public int getPlayer()
{   if (onePlaysNext)
        return PLAYER_ONE;
    else return PLAYER_TWO;
} // getPlayer()
Another advantage of named constants (over literals) is that their use makes the program easier to modify and maintain. For example, suppose that we decide to change OneRowNim so that the maximum number of sticks that can be picked up is 4 instead of 3. If we used literal values, we would have to change all occurrences of 4 that were used to represent the maximum pick up. If we used a named constant, we need only change its declaration to:
public static final int MAX_PICKUP = 4;
So far, all of the examples we have presented show why named constants (but not necessarily class constants) are useful. Not all constants are class constants. That is, not all constants are declared static. However, the idea of associating constants with a class makes good sense. In addition to saving memory resources, by creating just a single copy of the constant, constants such as MAX_STICKS and PLAYER_ONE make more conceptual sense to associate with the class itself rather than with any particular OneRowNim instance.
Class constants are used extensively in the Java class library. For example, Java’s various built-in colors are represented as constants of the java.awt.Color class —Color.blue and Color.red. Similarly, java.awt.Label uses int constants to specify how a label’s text should be aligned: Label.CENTER.
Another advantage of class constants is that they can be used before instances of the class exist. For example, a class constant (as opposed to an instance constant) may be used during object instantiation:
OneRowNim game = new OneRowNim(OneRowNim.MAX_STICKS);
Note how we use the name of the class to refer to the class constant. Of course, MAX_STICKS has to be a public variable in order to be accessible outside the class. To use MAX_STICKS as a constructor argument it has to be a class constant because at this point in the program there are no OneRowNim instances. A new version of OneRowNim that uses class constants is shown in Listing 5.7.15.
It is important to note that Java also allows class constants to be referenced through an instance of the class. Thus, once we have instantiated game, we can refer to MAX_STICKS with either OneRowNim.MAX_STICKS or game.MAX_STICKS.
public class OneRowNim
{   public static final int PLAYER_ONE = 1;
    public static final int PLAYER_TWO = 2;
    public static final int MAX_PICKUP = 3;
    public static final int MAX_STICKS = 11;
    public static final boolean GAME_OVER = false;
    private int nSticks = MAX_STICKS;
    private boolean onePlaysNext = true;
    public OneRowNim()
    {
    } //OneRowNim() constructor1
    public OneRowNim(int sticks)
    {   nSticks = sticks;
    }  // OneRowNim() constructor2
    public OneRowNim(int sticks, int starter)
    {   nSticks = sticks;
        onePlaysNext = (starter == PLAYER_ONE);
    }  // OneRowNim() constructor3
    public boolean takeSticks(int num)
    {   if (num < 1 || num > MAX_PICKUP || num > nSticks)
            return false;                // Error
        else                             // Valid move
        {   nSticks = nSticks - num;
            onePlaysNext = !onePlaysNext;
            return true;
        } //else
    }//takeSticks()
    public int getSticks()
    {   return nSticks;
    } //getSticks()
    public int getPlayer()
    {   if (onePlaysNext)
            return PLAYER_ONE;
        else return PLAYER_TWO;
    } //getPlayer()
    public boolean gameOver()
    {   return (nSticks <= 0);
    } // gameOver()
    public int getWinner()
    {   if (nSticks < 1)
            return getPlayer();
        else return 0;         // Game is not over
    } // getWinner()
    public String report()
    {   return ("Number of sticks left: " + getSticks()
          + "\nNext turn by player " + getPlayer() + "\n");
    }   // report()
  } // OneRowNim class
Listing 5.7.15. This version of OneRowNim uses named constants.

Exercises Self-Study Exercises

1. OneRowNim with Constants.
Complete the main method below to implement a command-line interface that uses the new version of OneRowNim making use of the MAX_STICKS and MAX_PICKUP in the main method.

Subsection 5.7.4 OBJECT-ORIENTED DESIGN: Information Hiding

The fact that our new versions of OneRowNim — we’ve developed two new versions in this chapter— are backward compatible with the previous version is due in large part to the way we have divided up its public and private elements. Because the new versions still present the same public interface, programs that use the OneRowNim class, such as the OneRowNimApp from Chapter  4 (Figure 4.5.2), can continue to use the class without changing a single line of their own code. To confirm this, see the Self-Study Exercise at the end of this section.
Although we have made significant changes to the underlying representation of OneRowNim, the implementation details — its data and algorithms — are hidden from other objects. As long as OneRowNim’s public interface remains compatible with the old version, changes to its private elements won’t cause any inconvenience to those objects that were dependent on the old version. This ability to change the underlying implementation without affecting the outward functionality of a class is one of the great benefits of the information hiding principle.
The lesson to be learned here is that the public parts of a class should be restricted to just those parts that must be accessible to other objects. Everything else should be private. Things work better, in Java programming and in the real world, when objects are designed with the principle of information hiding in mind.

Exercises Self-Study Exercise

1. OneRowNim UI.
To confirm that our new version of OneRowNim still works correctly with the user interfaces we developed in Chapter 4, compile and run it with OneRowNimApp in a development environment that allows user input. (Figure 4.5.2).

Subsection 5.7.5 Example: A Winning Algorithm for One Row Nim

Now that we have access to numeric data types and operators, lets develop an algorithm that can win the One Row Nim game. Recall that in Chapter 4 we left things such that when the computer moves, it always takes 1 stick. Let’s replace that strategy with a more sophisticated approach.
If you have played One Row Nim, you have probably noticed that in a game with 21 sticks, you can always win the game if you leave your opponent with 1, 5, 9, 13, 17, or 21 sticks.
This is obvious for the case of 1 stick. For the case where you leave your opponent 5 sticks, no matter what the opponent does, you can make a move that leaves the other player with 1 stick. For example, if your opponent takes 1 stick, you can take 3; if your opponent takes 2, you can take 2; and, if your opponent takes 3, you can take 1. In any case, you can win the game by making the right move, if you have left your opponent with 5 sticks. The same arguments apply for the other values: 9, 13, 17, and 21.
What relationship is common to the numbers in this set? Notice that if you take the remainder after dividing each of these numbers by 4 you always get 1:
1 % 4  == 1
5 % 4  == 1
9 % 4  == 1
13 % 4  == 1
17 % 4  == 1
21 % 4  == 1
Thus, we can base our winning strategy on the goal of leaving the opponent with a number of sticks, N, such that N % 4 equals 1.
To determine how many sticks to take in order to leave the opponent with N, we need to use a little algebra. Let’s suppose that sticksLeft represents the number of sticks left before our turn. The first thing we have to acknowledge is that if sticksLeft % 4 == 1, then we have been left with 1, 5, 9, 13, and so on, sticks, so we cannot force a win. In that case, it doesn’t matter how many sticks we pick up. Our opponent should win the game.
So, let’s suppose that sticksLeft % 4 != 1, and let M be the number of sticks to pickup in order to leave our opponent with N, such that N % 4 == 1. Then we have the following two equations:
sticksLeft - M == N
N % 4 == 1
We can combine these into a single equation, which can be simplified as follows:
(sticksLeft - M)  % 4 == 1
If sticksLeft - M leaves a remainder of 1 when divided by 4, that means that sticksLeft - M is equal to some integer quotient, Q times 4 plus 1:
(sticksLeft - M)   ==  (Q * 4) + 1
By adding M to both sides and subtracting 1 from both sides of this equation, we get:
(sticksLeft - 1)   ==  (Q * 4) + M
This equation is saying that (sticksLeft - 1) % 4 == M. That is, that when you divide sticksLeft-1 by 4, you will get a remainder of M, which is the number of sticks you should pick up. Thus, to decide how many sticks to take, we want to compute:
M == (sticksLeft -1) % 4
To verify this, let’s look at some examples:
sticksLeft     (sticksLeft -1) % 4     sticksLeft
  Before                                  After
  ----------------------------------------------------
    9            (9-1) % 4 == 0         Illegal Move
    8            (8-1) % 4 == 3         5
    7            (7-1) % 4 == 2         5
    6            (6-1) % 4 == 1         5
    5            (5-1) % 4 == 0         Illegal Move
The examples in this table show that when we use (sticksLeft-1 % 4) to calculate our move, we always leave our opponent with a losing situation. Note that when sticksLeft equals 9 or 5, we can’t apply this strategy because it would lead to an illegal move.
Let’s now convert this algorithm into Java code. In addition to incorporating our winning strategy, this move() method makes use of two important Math class methods:
public int move()
{ int sticksLeft = nim.getSticks();   // Get number of sticks
  if (sticksLeft % (nim.MAX_PICKUP + 1) != 1)   // If winnable
    return (sticksLeft - 1) % (nim.MAX_PICKUP +1);
  else {                                // Else pick random
    int maxPickup = Math.min(nim.MAX_PICKUP, sticksLeft);
    return 1 + (int)(Math.random() * maxPickup);
  }
}
The move() method will return an int representing the best move possible. It begins by getting the number of sticks left from the OneRowNim object, which is referred to as nim in this case. It then checks whether it can win by computing (sticksLeft-1) % 4. However, note that rather than use the literal value 4, we use the named constant MAX_PICKUP, which is accessible through the nim object.
This is an especially good use for the class constant because it makes our algorithm completely general — that is, our winning strategy will continue to work even if the game is changed so that the maximum pickup is 5 or 6.
The then clause computes and returns (sticksLeft-1) \nim.MAX_PICKUP+1, but here again it uses the class constant.
The else clause would be used when it is not possible to make a winning move. In this case we want to choose a random number of sticks between 1 and some maximum number. The maximum number depends on how many sticks are left. If there are more than 3 sticks left, then the most we can pick up is 3, so we want a random number between 1 and 3. However, if there are 2 sticks left, then the most we can pick up is 2 and we want a random number between 1 and 2. Note how we use the Math.min() method to decide the maximum number of sticks that can be picked up:
int maxPickup = Math.min(nim.MAX_PICKUP, sticksLeft);
The min() method returns the minimum value between its two arguments.
Finally, note how we use the Math.random() method to calculate a random number between 1 and the maximum:
1 + (int)(Math.random() * maxPickup);
The random() method returns a real number between 0 and 0.999999 — that is, a real number between 0 and 1 but not including 1:
0 <= Math.random() < 1.0
If we multiply Math.random() times 2, the result would be a value between 0 and 1.9999999. Similarly, if we multiplied it by 3, the result would be a value between 0 and 2.9999999. In order to use the random value, we have to convert it into an integer, which is done by using the (int) cast operator:
(int)(Math.random() * maxPickup);
Recall that when a double is cast into an int, Java just throws away the fractional part. Therefore, this expression will give us a value between 0 and maxPickup-1. If maxPickup is 3, this will give a value between 0 and 2, whereas we want a random value between 1 and 3. To achieve this desired value, we merely add 1 to the result. Thus, using the expression
1 + (int)(Math.random() * maxPickup)
gives us a random number between 1 and maxPickup, where maxPickup is either 1, 2, or 3, depending on the situation of the game at that point.

Exercises Self-Study Exercises

Figure 5.7.17. The NimPlayer class.
1. NimPlayer.
This version of OneRowNim plays NimPlayer with the winning strategy against the RndPlayer which picks randomly. Implement a class named NimPlayer that incorporates the move() method with the winning strategy designed in this section. Use the RndPlayer below as a guide. The class should implement the design shown in Figure 5.7.17. That is, in addition to the move() method, it should have an instance variable, nim, which will serve as a reference to the OneRowNim game. Its constructor method should take a OneRowNim parameter, allowing the NimPlayer to be given a reference when it is instantiated.
2. NimPlayer UI.
Using a development environment which allows user input, modify OneRowNim’s command-line interface to play One Row Nim between the user and the computer, where the NimPlayer implemented in the previous exercise represents the computer.
You have attempted of activities on this page.
PrevTopNext