Section 20.5 Using the Loop Variable
In previous pages, we have seen examples that are repetitive, but where each line has a slight change, like this sequence of calls to polygon:
...
polygon(mia, 6, 100)
polygon(mia, 5, 100)
polygon(mia, 4, 100)
polygon(mia, 3, 100)
In situations like that, it would be nice to use a loop to repeat the lines instead of typing them out one by one. But to do so, we need to use a variable for the value that changes. Something like polygon(mia, sides, 100) where sides is set to the values 6, 5, 4, 3 in successive calls.
We can do this by making use of the loop variable. It is the variable that is used to store each value in the list that the loop is iterating over. This program shows using two loops. In the first one, the loop variable is called x and is used to count from 0 to 4. In the second, the loop variable is called y and counts from 0 to 9.
Subsection 20.5.1 Range Recipes
That gives us a way to count through a series of numbers. But what if we want, like with the polygon example, to count from 6 down to 3? Or to count from 10 to 100 by 10’s? To do these tasks, we can use a three-parameter version of range:
range(startValue, stopValue, step)
This version of range begins from the startValue, increases by step with each value, and stops when it hits stopValue (but does not actually include the stopValue). If the step is negative, range will count down from startValue to stopValue .
Check Your Understanding
Checkpoint 20.5.2.
Which range recipe would generate the sequence: 2, 5, 8, 11?
range(2, 11, 3)
If the stopValue is 11, it will not actually generate 11.
range(2, 12, 3)
This will not cause an error.
range(3, 12, 2)
The startValue is the first parameter. This recipe would start with 3.
range(2, 3, 11)
This recipe starts at 2, counts by 11, and stops at 3. It would only include 2.
Subsection 20.5.2 Range Recipes With Turtles
We can now use the complex version of range to write a turtle program that repeats steps but uses a different value for a variable during each repetition.
The program below will use the stamp procedure to leave a copy of itself on the screen that will remain after the turtle has moved somewhere else. It also uses the shape procedure to change the turtle’s icon from the default triangle to an actual turtle.
The loop, for size in range(5, 60, 2):, says to count by 2’s from 5 to 59. The loop variable is called size and is used to control how far forward the turtle moves in each repetition.
All except one of the shapes you see on the screen here are copies of the turtle shape created by stamp. But the program still only has one turtle instance — can you figure out which one is the real tess? (Hint: if you’re not sure, write a new line of code after the for loop to change tess’ color, or to put her pen down and draw a line, or to change her shape, etc…)
Mixed up program
Checkpoint 20.5.4.
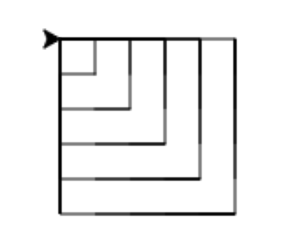
The following program creates a square spiral as shown below. To do so, we must draw sides of length 0, 5, 10, 15, … 195. After drawing each side, we will turn to get ready for the next side.
Arrange and indent the blocks correctly. You will not use them all.
from turtle import *
nikea = Turtle()
nikea.color("blue")
---
for x in range(0, 200, 5):
---
for x in range(0, 195, 5): #paired
---
for x in range(0, 205, 5): #paired
---
nikea.forward(x)
---
nikea.forward(size) #paired
---
nikea.forward(195) #paired
---
nikea.right(90)
---
nikea.right(x) #paired
---
nikea.right(size) #paired
Checkpoint 20.5.5.
The following program defines a square procedure and then uses it to draw squares of size 20, 40, 60, 80, and 100.
Arrange and indent the blocks correctly. You will not use them all.
def square(turtleName, size):
---
for side in range(4):
---
for side in range(size): #paired
---
turtleName.forward(size)
turtleName.right(90)
---
turtleName.forward(x)
turtleName.right(90) #paired
---
# main program
from turtle import *
jose = Turtle()
jose.speed(10)
---
for x in range(20, 101, 20):
---
for x in range(20, 100, 20): #paired
---
square(jose, x)
---
square(jose, size) #paired
You have attempted
of
activities on this page.