Skip to main content
Logo image

Intermediate Algebra Functions and Graphs

Katherine Yoshiwara

Section A.2 Chapter 2 Applications of Linear Models

Subsection A.2.1 Linear Regression

Subsubsection A.2.1.1 Read a scatterplot

We read the coordinates of points on a scatterplot the same way we do for any other graph.
🔗
Example A.2.1.
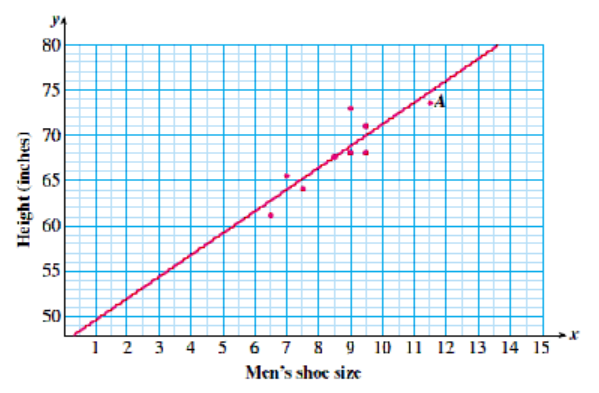
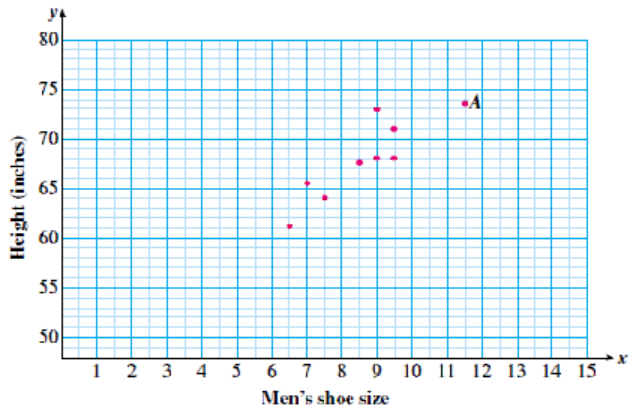
The scatterplot shows the height and shoe size of a group of men.
  1. State the height and shoe size of the man represented by point \(A\text{.}\)
    🔗
  2. Find the heights of two men with the same shoe size.
    🔗
🔗
scatterplot
Solution.
  1. The man represented by point \(A\) has shoe size \(11 \frac{1}{2}\) and is \(73 \frac{1}{2}\) inches tall.
    🔗
  2. There are two men with shoe size 9, with heights 68 and 73 inches. There are also two men with shoe size \(9 \frac{1}{2}\text{,}\) with heights 68 and 71 inches.
    🔗
🔗
🔗
🔗
Checkpoint A.2.2.
The scatterplot shows the heights of dance partners in a ballroom dance class.
  1. How tall is the shortest woman?
    🔗
  2. What are the heights of the three partners of the 65-inch tall women?
    🔗
🔗
scatterplot
Answer.
  1. 59 in
    🔗
  2. \(68 \frac{1}{2}\text{,}\) \(70\text{,}\) and \(71\) in
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.1.2 Sketch a line of best fit

Of course, the points on a scatterplot may not lie on a straight line. But if they seem to cluster near a line, we can try to find that line.
🔗
Example A.2.3.
Sketch a line of best fit for the scatterplot above.
🔗
Solution.
We draw a line that lies as close as possible to all of the data points. As a rule of thumb, we try to keep equal numbers of points on each side of the line.
🔗
scatterplot
🔗
🔗
Checkpoint A.2.4.
Which of the lines fits the scatterplot best?
🔗
scatterplot
Answer.
Line L
🔗
🔗
🔗
🔗

Subsubsection A.2.1.3 Fit a line through two points

If we don’t know the slope of a line, but we do know two points on the line, we can calculate the slope first and then use the point-slope formula.
🔗
Example A.2.5.
Find an equation for the line that passes through \((2,-1)\) and \((-1,3)\text{.}\)
🔗
Solution.
We solve this problem in two steps: First, find the slope of the line, and then use the point-slope formula.
🔗
Step 1: Let \((x_1,y_1)=(2,-1)\) and \((x_2,y_2)=(-1,3)\text{.}\) Use the slope formula to find
\begin{align*} m \amp = \dfrac{y_2-y_1}{x_2-x_1}\\ \amp = \dfrac{3-(-1)}{-1-2} = \dfrac{4}{-3} = \dfrac{-4}{3} \end{align*}
🔗
line thru (2,-1) and (-1,3)
Step 2: Apply the point-slope formula with \(m=\dfrac{-4}{3}\) and \((x_1,y_1)=(2,-1)\text{.}\) (We can use either point in the formula.) Then
\begin{equation*} \dfrac{y-y_1}{x-x_1} = m~~~~~~~~\text{becomes}~~~~~~~~\dfrac{y-(-1)}{x-2} = \dfrac{-4}{3} \end{equation*}
Cross-multiply to find
\begin{align*} 3(y+1) \amp = -4(y-2) \amp \amp \blert{\text{Apply the distributive law.}}\\ 3y+3 \amp = -4x+8 \amp \amp \blert{\text{Solve for}~y.}\\ 3y \amp = -4x+5\\ y \amp = \dfrac{-4}{3}x + \dfrac{5}{3} \end{align*}
🔗
🔗
🔗
Checkpoint A.2.6.
Find an equation for the line that passes through \((-6,-1)\) and \((1,3)\text{.}\)
🔗
Answer.
Step 1: Compute the slope.
🔗
Step 2: Use the point-slope formula.
\begin{equation*} y=\dfrac{4}{7}x+\dfrac{17}{7} \end{equation*}
🔗
🔗
🔗
🔗
🔗

Subsection A.2.2 Linear Systems

Subsubsection A.2.2.1 Write equations in two variables

Applied problems that involve more than one unknown are often easier to model and solve with a system of equations.
🔗
Example A.2.7.
Write equations about the number of tables and the number of chairs:
  1. There are four chairs for each table.
    🔗
  2. Chairs cost $125 each; a table costs $350. Darryl spent $10,200 on tables and chairs.
    🔗
🔗
Solution.
Let \(x\) be the number of tables and \(y\) the number of chairs.
  1. The number of chairs is 4 times the number of tables: \(~y=4x\text{.}\)
    🔗
  2. \(\displaystyle 125y+350x=10,200\)
    🔗
🔗
🔗
🔗
Example A.2.8.
Write equations about the dimensions of a rectangle:
  1. The perimeter of the rectangle is 42 meters.
    🔗
  2. The length is 3 meters more than twice the width.
    🔗
🔗
Solution.
Let \(x\) be the width of the rectangle and \(y\) its length.
  1. \(\displaystyle 2x+2y=42\)
    🔗
  2. \(\displaystyle y=3+2x\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.9.
Write equations about the number of calories in a hamburger and in a chocolate shake.
  1. A hamburger and a chocolate shake together contain 1020 calories.
    🔗
  2. Two shakes and three hamburgers contain 2710 calories.
    🔗
🔗
Answer.
  1. \(\displaystyle x+y=1020\)
    🔗
  2. \(\displaystyle 3x+2y=2710\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.10.
Write equations about the vertex angle and the base angles of an isosceles triangle.
  1. The vertex angle is \(15 \degree\) less than each base angle.
    🔗
  2. The sum of the angles in a triangle is \(180 \degree\text{.}\)
    🔗
🔗
Answer.
  1. \(\displaystyle y=x-5\)
    🔗
  2. \(\displaystyle 2x+y=180\)
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.2.2 Identify the solution of a system

Recall that a solution to a system makes each equation in the system true.
🔗
Example A.2.11.
Decide whether \((3,-2)\) is a solution of the system
\begin{gather*} x = 5y+13\\ 2x+3y=0 \end{gather*}
🔗
Solution.
A solution must satisfy both equations. We substitute \(x=\alert{3}\) and \(y=\alert{-2}\) into the equations.
\begin{align*} \alert{3} = 5(\alert{-2})+13 ? \amp \amp \text{Yes}\\ 2(\alert{3})+3(\alert{-2})=0 ? \amp \amp \text{Yes} \end{align*}
Yes, \((3,-2)\) is a solution
🔗
🔗
🔗
Example A.2.12.
Find the solution of the system graphed below.
🔗
Linear system
Solution.
The solution must lie on both graphs, so it is the intersection point, \(P\text{.}\) The coordinates of point \(P\) are \((50, 1300)\text{,}\) so the solution of the system is \(t=50,~y=1300\text{.}\)
🔗
🔗
🔗
Checkpoint A.2.13.
Decide whether \((-3,-2)\) is a solution of the system
\begin{align*} x + 3y \amp = -9\\ 3x+2y \amp = -5 \end{align*}
🔗
Answer.
No
🔗
🔗
🔗
Checkpoint A.2.14.
Find the solution of the system graphed below.
🔗
Linear system
Answer.
\((300, 24)\)
🔗
🔗
🔗
🔗

Subsubsection A.2.2.3 Use the formula for profit, \(P=R-C\)

Profit.
To find the profit earned by a company we subtract the costs from the revenue.
\begin{equation*} \text{Profit} = \text{Revenue} - \text{Cost}~~~~~~~~P=R-C \end{equation*}
🔗
🔗
"Revenue" is the amount of money a company takes in from selling its product. A negative profit is the same as a loss.
🔗
Example A.2.15.
The owner of a sandwich shop spent $800 last week for labor and supplies. She received $1150 in revenue. What was her profit?
🔗
Solution.
We evaluate the formula with \(R=1150\) and \(C=800\) to find
\begin{align*} P \amp = R-C\\ \amp = 1150 - 800 = 350 \end{align*}
The owner’s profit was $350.
🔗
🔗
🔗
Example A.2.16.
EcoGreen made $1848 profit on low-flow shower heads last year, and spent $3426 in costs. What was their revenue from shower heads?
🔗
Solution.
We usse the profit formula and solve the equation
\begin{equation*} 1848 = R - 3246 \end{equation*}
to find that \(R=5094\text{.}\) Their revenue was $5094.
🔗
🔗
🔗
Checkpoint A.2.17.
  1. The Earth Alliance made $6000 in revenue from selling tickets to Earth Day, an educational event for children. Write an expression for their profit in terms of their costs.
    🔗
  2. What was their profit if their costs were $2500?
    🔗
🔗
Answer.
  1. \(\displaystyle P=6000-C \)
    🔗
  2. $3500
    🔗
🔗
🔗
🔗
Checkpoint A.2.18.
Last week Moe’s Auto Shop took in $5400 in revenue, but experienced a loss of $800. What were Moe’s costs last week?
🔗
Answer.
$6200
🔗
🔗
🔗
🔗
🔗

Subsection A.2.3 Algebraic Solution of Systems

Some familiar formulas are useful in writing equations to solve a problem.
🔗

Subsubsection A.2.3.1 Use the interest formula, \(I=Pr\)

Example A.2.19.
You have $5000 to invest for one year. You want to put part of the money into bonds that pay 7% interest, and the rest of the money into stocks that involve some risk but will pay 12% if successful. Now suppose you decide to invest \(x\) dollars in stocks and \(y\) dollars in bonds.
  1. Use the interest formula, \(I=Pr\text{,}\) to write expressions for the interest earned on the bonds and on the stocks.
    🔗
  2. Write an equation about the amount invested.
    🔗
  3. Write an equation to say that the total interest earned was $400.
    🔗
🔗
Solution.
  1. Stocks: \(I=0.12x;~~~\)Bonds: \(I=0.07y\)
    🔗
    🔗
  2. \(\displaystyle x+y=500\)
    🔗
  3. \(\displaystyle 0.12x+0.07y=400\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.20.
Mort invested money in two accounts, a savings plan that pays 8% interest and a mutual fund that pays 7% interest. He put twice as much money in the savings plan as in the mutual fund. At the end of the year Mort’s total interest income was $345. How much did he invest in each account?
  1. Use the interest formula to write expressions for the interest Mort earned on the savings plan and the interest he earned on the mutual fund.
    🔗
  2. Write an equation about the amount Mort invested.
    🔗
  3. Write an equation about the interest Mort earned.
    🔗
🔗
Answer.
  1. \(\displaystyle 0.04x;~~0.09y\)
    🔗
  2. \(\displaystyle x+y=2000\)
    🔗
  3. \(\displaystyle 0.09y=37+0.04x\)
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.3.2 Use the percent formula, \(P=rW\)

Example A.2.21.
A pharmacist has on hand a solution of a certain medication at 40% strength, but she needs 48 ounces of the medication at 75% strength for a prescription. She decides to add a pure form of the medication to the 40% solution. How much of the each strength solution should she add to make a mixture of 75% strength?
  1. Choose variables for the unknown quantities.
    🔗
  2. Write an equation about the amount of 75% solution.
    🔗
  3. Use the percent formula, \(P=rW\text{,}\) to calculate the amount of the medication in the original solution.
    🔗
  4. Use the percent formula to calculate the amount of the medication in the mixture.
    🔗
  5. Write an equation about the amount of medication.
    🔗
🔗
Solution.
  1. Let \(x\) stand for tthe amount of 40% solution and \(y\) for the pure solution.
    🔗
  2. \(\displaystyle x+y=48\)
    🔗
  3. \(\displaystyle 0.40(20)=8\)
    🔗
  4. \(\displaystyle P=rW = 0.40x\)
    🔗
  5. \(\displaystyle P=rW=0.0.75(48) = 36\)
    🔗
  6. \(\displaystyle 0.40x+y = 36\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.22.
A pet store owner wants to mix a 12% saltwater solution and a 30% saltwater solution to obtain 90 liters of a 24% solution. He uses \(x\) quarts of the 12% solution and \(y\) quarts of the 30% solution.
  1. Write an equation about the total amount of saltwater.
    🔗
  2. Use the percent formula to write expressions about the amount of salt in each original solution.
    🔗
  3. How many liters of salt are in the mixture?
    🔗
  4. Write an equation about the amount of salt.
    🔗
🔗
Answer.
  1. \(\displaystyle x+y=90\)
    🔗
  2. \(\displaystyle 0.20x;~~0.30y\)
    🔗
  3. \(\displaystyle 0.24(90)\)
    🔗
  4. \(\displaystyle 0.20x+0.30y=0.24(90)\)
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.3.3 Use the distance formula, \(d=rt\)

Example A.2.23.
A river steamer requires 3 hours to travel 24 miles upstream and 2 hours for the return trip downstream. Let \(x\) be the speed of the current and \(y\) the speed of the steamer in still water.
  1. Write an equation about the upstream trip.
    🔗
  2. Write an equation about the downstream trip.
    🔗
🔗
Solution.
  1. The speed of the steamer aginst the current is \(r=y-x\text{,}\) so \(~3(y-x)=24\)
    🔗
  2. The speed of the steamer with the current is \(r=y+x\text{,}\) so \(~2(y+x)=24\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.24.
A yacht leaves San Diego and heads south, traveling at 25 miles per hour. Six hours later a Coast Guard cutter leaves San Diego traveling at 40 miles per hour and pursues the yacht. Let \(x\) be the time it takes the cutter to catch the yacht, and \(y\) the distance it traveled.
  1. Write an equation about the yacht’s journey.
    🔗
  2. Write an equation about the cutter’s journey.
    🔗
🔗
Answer.
  1. \(\displaystyle 25(x+6)=y\)
    🔗
  2. \(\displaystyle 40x=y\)
    🔗
🔗
🔗
🔗
🔗
🔗

Subsection A.2.4 Gaussian Reduction

Subsubsection A.2.4.1 Write an equation in standard form

Before we can use Gaussian reduction, we must write each equation in standard form.
🔗
Example A.2.25.
Write the equation in standard form.
  1. \(\displaystyle 3y-7=4z+x\)
    🔗
  2. \(\displaystyle 6=-5z+2x\)
    🔗
🔗
Solution.
The standard form is \(ax+by+cz=d\text{.}\) We add or subtract appropriate terms on both sides of the equation.
  1. \(-x+3y-4z=7,~\) or \(~x-3y+4z=-7\)
    🔗
  2. \(2x+0y-5z=6,~\) or \(~-2x+0y+5z=-6\)
    🔗
🔗
🔗
🔗
Checkpoint A.2.26.
Write the equation in standard form.
  1. \(\displaystyle 5-3x+4y=2z\)
    🔗
  2. \(\displaystyle y=8-2z\)
    🔗
🔗
Answer.
  1. \(\displaystyle -3x+4y-2z=-5\)
    🔗
  2. \(\displaystyle 0x+y+2z=8\)
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.4.2 Clear fractions from an equation

It is easier to use Gaussian reduction if the equations have integer coefficients.
🔗
Example A.2.27.
Write the equation with integer coefficients.
  1. \(\displaystyle \dfrac{1}{4}x+z=\dfrac{3}{4}\)
    🔗
  2. \(\displaystyle \dfrac{2}{3}x-2y+\dfrac{1}{2}z=3\)
    🔗
🔗
Solution.
  1. We multiply both sides of the equation by \(\alert{4}\text{.}\)
    \begin{align*} \alert{4} \cdot \left(\dfrac{1}{4}x+z\right) \amp = \left(\dfrac{3}{4}\right) \cdot \alert{4}\\ x+4z \amp = 3 \end{align*}
    🔗
    🔗
  2. We multiply both sides of the equation by the LCD of the fractions, \(\alert{6}\text{.}\)
    \begin{align*} \alert{6} \cdot \left(\dfrac{2}{3}x-2y+\dfrac{1}{2}z\right) \amp = (3) \cdot \alert{6}\\ 4x-12y+3z \amp = 18 \end{align*}
    🔗
    🔗
🔗
🔗
🔗
Checkpoint A.2.28.
Write the equation with integer coefficients.
  1. \(\displaystyle \dfrac{1}{5}x-\dfrac{2}{5}y+z=-1\)
    🔗
  2. \(\displaystyle \dfrac{3}{4}x-y+\dfrac{5}{6}z=6\)
    🔗
🔗
Answer.
  1. \(\displaystyle x-2y+5z=-5\)
    🔗
  2. \(\displaystyle 9x-12y+10z=72\)
    🔗
🔗
🔗
🔗
🔗

Subsubsection A.2.4.3 Write a 3x3 linear system

Example A.2.29.
Write a 3x3 linear system for the following problem:
🔗
Ace, Inc. produces three types of wooden rackets: tennis rackets, Ping-Pong paddles, and squash rackets. After the pieces are cut, each racket requires three phases of production: gluing, sanding and finishing. A tennis racket takes 3 hours to glue, 2 hours to sand, and 3 hours to finish. A Ping-Pong paddle takes 1 hour to glue, 1 hour to sand, and 1 hour to finish. A squash racket takes 2 hours to glue, 2 hours to sand, and 2.5 hours to finish. Ace has available 95 labor-hours for gluing, 75 labor-hours for sanding, and 100 labor-hours for finishing per day. How many of each racket should it make in order to use all the available time?
🔗
Solution.
Let \(x\text{,}\) \(y\text{,}\) and \(z\) stand for the number of tennis rackets, Ping-Pong paddles, and squash rackets, respectively. Write three equations about the number of hours needed for each phase:
\begin{align*} \text{Gluing:}~~~~~~ \amp 3x+y+2z = 95\\ \text{Sanding:}~~~~~~ \amp 2x+y+2z = 75\\ \text{Finsihing:}~~~~~~ \amp 3x+y+2.5z = 100 \end{align*}
🔗
🔗
🔗
Checkpoint A.2.30.
Write a 3x3 linear system for the following problem:
🔗
A box contains $6.25 in nickels, dimes, and quarters. There are 85 coins in all, with 3 times as many nickels as dimes. How many coins of each kind are there?
🔗
Answer.
Let \(x\text{,}\) \(y\text{,}\) and \(z\) stand for the number of nickels, dimes, and quarters, respectively.
🔗
\begin{align*} x+y+z \amp = 85\\ x \amp = 3y\\ 5x + 10y + 25z \amp = 625 \end{align*}
🔗
🔗
🔗
🔗
🔗

Subsection A.2.5 Linear Inequalities in Two Variables

Subsubsection A.2.5.1 Solve a linear inequality

Before we solve inequalities in two variables, let’s review solving linear inequalities in one variable.
🔗
Example A.2.31.
Solve \(~3k-13 \lt 5+6k\)
🔗
Solution.
We begin just as we do to solve an equation. The only difference is that we must reverse the direction of the inequality if we multiply or divide by a negative number.
\begin{align*} 3k-13 \amp \lt 5+6k \amp \amp \blert{\text{Subtract}~6k~\text{from both sides.}} \\ -3k \amp \lt 18 \amp \amp \blert{\text{Divide both sides by}~-3.}\\ k \amp \gt -6 \amp \amp \blert{\text{Don't forget to reverse the inequality.}} \end{align*}
In interval notation, the solution set is \((-6,\infty)\text{.}\)
🔗
🔗
🔗
Checkpoint A.2.32.
Solve \(~~4(3a-7) \gt -18+2a.~~\) Write the solution with interval notation.
🔗
Answer.
\((1, \infty) \)
🔗
🔗
🔗
Checkpoint A.2.33.
Solve \(~~4 \le \dfrac{-3x}{4}-2.~~\) Write the solution with interval notation.
🔗
Answer.
\((-\infty,8] \)
🔗
🔗
🔗
Checkpoint A.2.34.
Solve \(~~15 \ge -6+3m \ge -6.~~\) Write the solution with interval notation.
🔗
Answer.
\([0,7] \)
🔗
🔗
🔗
Checkpoint A.2.35.
Solve \(~~\dfrac{-9}{2} \lt \dfrac{5-2n}{-4} \le -1.~~\) Write the solution with interval notation.
🔗
Answer.
\(\left(\dfrac{-13}{2}, \dfrac{1}{2}\right] \)
🔗
🔗
🔗
🔗

Subsubsection A.2.5.2 Graph a line

The boundary of the solution set for a linear inequality in two variables is made up of portions of straight lines.
🔗
Example A.2.36.
Use the most convenient method to graph the equation.
  1. \(\displaystyle 5x-10y=750\)
    🔗
  2. \(\displaystyle y=400-25x\)
    🔗
🔗
Solution.
  1. This equation is in the form \(Ax+By=C\text{,}\) so the intercept method of graphing is convenient. The intercepts are \((150,0)\) and \((0,-75)\text{.}\) The graph is shown below.
    🔗
    line
    🔗
  2. This equation is in the form \(y=mx+b\text{,}\) so the slope-intercept method of graphing is convenient. The \(y\)-intercept is \((0,400)\text{,}\) and the slope is \(-25\text{.}\) The graph is shown below.
    🔗
    line
    🔗
🔗
🔗
🔗
Checkpoint A.2.37.
Graph the equation \(~~24x+9y=432\)
🔗
Answer.
line
🔗
🔗
Checkpoint A.2.38.
Graph the equation \(~~y=12x+60\)
🔗
Answer.
line
🔗
🔗
Checkpoint A.2.39.
Graph the equation \(~~y=600-1.25x\)
🔗
Answer.
line
🔗
🔗
Checkpoint A.2.40.
Graph the equation \(~~45x-30y=15\)
🔗
Answer.
line
🔗
🔗
🔗

Subsubsection A.2.5.3 Solve a 2x2 system

To find the vertices of the boundary of the solution set, we solve a linear 2x2 system.
🔗
Example A.2.41.
Use substitution to solve the system:
\begin{align*} 3y-2x \amp = 3\\ x-2y \amp = -2 \end{align*}
🔗
Solution.
We start by solving the second equation for \(x\) to get \(x=2y-2\text{.}\) Then we substitute this expression for \(x\) into the first equation, which gives us
\begin{equation*} 3y-2(2y-2)=3 \end{equation*}
We solve this equation for \(y\) to find \(y=1\text{.}\) Finally, we substitute \(y=1\) into our first step to find
\begin{equation*} x=2(1)-2=0 \end{equation*}
The solution is \(x=0,~y=1\text{,}\) or \((0,1)\text{.}\)
🔗
🔗
🔗
Example A.2.42.
Use elimination to solve the system:
\begin{align*} 2x+3y \amp = -1\\ 3x+5y \amp = -2 \end{align*}
🔗
Solution.
We multiply the first equation by 3 and the second equation by \(-2\) in order to eliminate \(x\text{.}\)
\begin{align*} 6x+9y \amp = -3\\ -6x-10y \amp = 4 \end{align*}
Adding these two equations gives us \(-y=1\text{,}\) or \(y=-1\text{.}\) Finally, we substitute \(y=-1\) into either equation (we choose the first equation), and solve for \(x\text{.}\)
\begin{align*} 2x+3(-1) \amp = -1\\ 2x-3 \amp = -1 \end{align*}
We find\(x=1\text{,}\) so the solution is \(x=1,~y=-1\text{,}\) or \((1,-1)\text{.}\)
🔗
🔗
🔗
Checkpoint A.2.43.
Solve the system:
\begin{align*} y \amp = 2x+1\\ 2x+3y \amp = -21 \end{align*}
🔗
Answer.
\((-3,-5)\)
🔗
🔗
🔗
Checkpoint A.2.44.
Solve the system:
\begin{align*} x+4y \amp = 1\\ 2x+3y \amp = -3 \end{align*}
🔗
Answer.
\((-3,1)\)
🔗
🔗
🔗
Checkpoint A.2.45.
Solve the system:
\begin{align*} 2x+7y \amp = -19\\ 5x-3y \amp = 14 \end{align*}
🔗
Answer.
\((1,-3)\)
🔗
🔗
🔗
Checkpoint A.2.46.
Solve the system:
\begin{align*} 4x+3y \amp = -19\\ 5x+15 \amp = -2y \end{align*}
🔗
Answer.
\((-1,-5)\)
🔗
🔗
🔗
🔗
🔗
You have attempted of activities on this page.
🔗
PrevTopNext