Chapter 8 Polynomial and Rational Functions
The graphs of linear functions, quadratic functions, power functions, and exponential all have a characteristic shape. On the other hand, the family of polynomial funcions has graphs that represent a huge variety of different shapes.
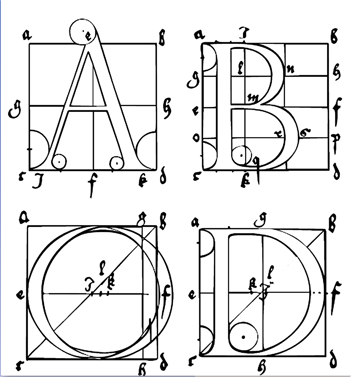
Ever since Gutenberg’s invention of movable type in 1455, artists and printers have been interested in the design of pleasing and practical fonts. In 1525, Albrecht Durer published On the Just Shaping of Letters, which set forth a system of rules for the geometric construction of Roman capitals. The letters shown above are examples of Durer’s font. Until the twentieth century, a ruler and compass were the only practical design tools, so straight lines and circular arcs were the only geometric objects that could be accurately reproduced.
With the advent of computers, complex curves and surfaces, such as the smooth contours of modern cars, can be defined precisely. In the 1960s the French automobile engineer Pierre Bézier developed a new design tool based on polynomials. Bézier curves are widely used today in all fields of design, from technical plans and blueprints to the most creative artistic projects.
The study of Bézier curves falls under the general topic of curve fitting, but these curves do not really have a scientific purpose. A scientist does not use Bézier curves to fit a function to data. Rather, Bézier curves have more of an artistic purpose. Computer programs like Illustrator, Freehand, and CorelDraw use cubic Bézier curves. The PostScript printer language and Type 1 fonts also use cubic Bézier curves, and TrueType fonts use quadratic Bézier curves.


