Inverse Variation.
\(y\) varies inversely with \(x\) if
\begin{equation*}
y = \dfrac{k}{x}\text{, }x \ne 0
\end{equation*}
where \(k\) is a positive constant.
| \(R\) | \(T\) |
| \(10\) | \(60\) |
| \(15\) | \(40\) |
| \(20\) | \(30\) |
| \(50\) | \(12\) |
| \(200\) | \(3\) |
| \(400\) | \(1.5\) |

| \(R\) | \(10\) | \(15\) | \(20\) | \(50\) | \(200\) | \(400\) |
| \(T\) | \(60\) | \(40\) | \(30\) | \(12\) | \(3\) | \(1.5\) |
| \(RT\) | \(600\) | \(600\) | \(600\) | \(600\) | \(600\) | \(600\) |
| \(R\) | \(1\) | \(2\) | \(10\) | \(20\) |
| \(I\) | \(\hphantom{0000} \) | \(\hphantom{0000} \) | \(\hphantom{0000} \) | \(\hphantom{0000} \) |
| \(R\) | \(1\) | \(2\) | \(10\) | \(20\) |
| \(I\) | \(120\) | \(60\) | \(12\) | \(6\) |

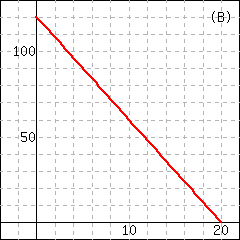
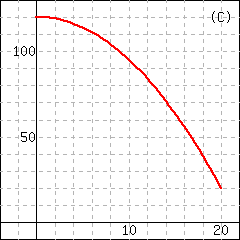
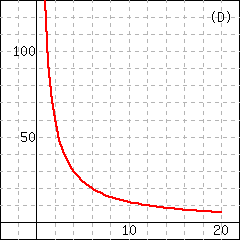



| \(m\) | \(0.05\) | \(0.20\) | \(0.25\) | \(0.4\) |
| \(H\) | \(240\) | \(15\) | \(9.6\) | \(3.75\) |
| \(m\) | \(0.05\) | \(0.20\) | \(0.25\) | \(0.4\) |
| \(H\) | \(240\) | \(15\) | \(9.6\) | \(3.75\) |


| \(x\) | \(4\) | \(\hphantom{\qquad}\) | \(20\) | \(30\) | \(\hphantom{\qquad}\) |
| \(y\) | \(\hphantom{\qquad}\) | \(15\) | \(6\) | \(\hphantom{\qquad}\) | \(3\) |
| \(x\) | \(4\) | \(8\) | \(20\) | \(30\) | \(40\) |
| \(y\) | \(30\) | \(15\) | \(6\) | \(4\) | \(3\) |
| \(x\) | \(0.2\) | \(\hphantom{\qquad}\) | \(2\) | \(4\) | \(\hphantom{\qquad}\) |
| \(y\) | \(\) | \(80\) | \(\hphantom{\qquad}\) | \(1.25\) | \(0.8\) |
| \(x\) | \(0.5\) | \(2\) | \(3\) | \(6\) |
| \(y\) | \(288\) | \(18\) | \(8\) | \(2\) |
| \(x\) | \(0.5\) | \(2\) | \(4\) | \(5\) |
| \(y\) | \(100.0\) | \(25.0\) | \(12.5\) | \(10.0\) |
| \(x\) | \(1\) | \(1.3\) | \(3\) | \(4\) |
| \(y\) | \(4.0\) | \(3.7\) | \(2.0\) | \(1.0\) |
| \(x\) | \(0.5\) | \(2\) | \(3\) | \(5\) |
| \(y\) | \(180.00\) | \(11.25\) | \(5.00\) | \(1.80\) |
| \(\text{Width (feet)} \) | \(2\) | \(2.5\) | \(3\) |
| \(\text{Length (feet)} \) | \(12\) | \(9.6\) | \(8\) |
| \(\text{Length}\times \text{Width} \) | \(\hphantom{00000}\) | \(\hphantom{00000}\) | \(\hphantom{00000}\) |
| \(\text{Width (feet)} \) | \(2\) | \(2.5\) | \(3\) |
| \(\text{Length (feet)} \) | \(12\) | \(9.6\) | \(8\) |
| \(\text{Length}\times \text{width} \) | \(\alert{24}\) | \(\alert{24}\) | \(\alert{24}\) |

| \(\text{Distance (Earth radii)} \) | \(1\) | \(2\) | \(4\) |
| \(\text{Force (newtons)} \) | \(9.8\) | \(2.45\) | \(0.6125\) |
| \(\text{Force}\times\text{distance}^2\) | \(\hphantom{00000}\) | \(\hphantom{00000}\) | \(\hphantom{00000}\) |
| \(d\) | \(1\) | \(2\) | \(12\) | \(24\) |
| \(B\) | \(\hphantom{0000} \) | \(\hphantom{0000} \) | \(\hphantom{0000} \) | \(\hphantom{0000} \) |
| \(d\) | \(1\) | \(2\) | \(12\) | \(24\) |
| \(B\) | \(\alert{88} \) | \(\alert{44} \) | \(\alert{7.3} \) | \(\alert{3.7} \) |


| Depth (m) | Temperature (\(\degree\)C) |
| \(200\) | \(20\) |
| \(400\) | \(10\) |
| \(1000\) | \(4\) |
| Length (cm) | Frequency |
| \(55\) | \(260\) |
| \(57.2\) | \(250\) |
| \(65\) | \(220\) |
| \(71.5\) | \(200\) |