Skip to main content
Logo image

Intermediate Algebra: Functions and Graphs

Katherine Yoshiwara

Appendix B Answers to Selected Exercises

1 Linear Models
1.1 Linear Models
1.1.3 Problem Set 1.1

Warm Up

1.1.3.1.
Answer.
  1. \(\displaystyle 5.5\)
  2. \(\displaystyle 12\)
1.1.3.3.
Answer.
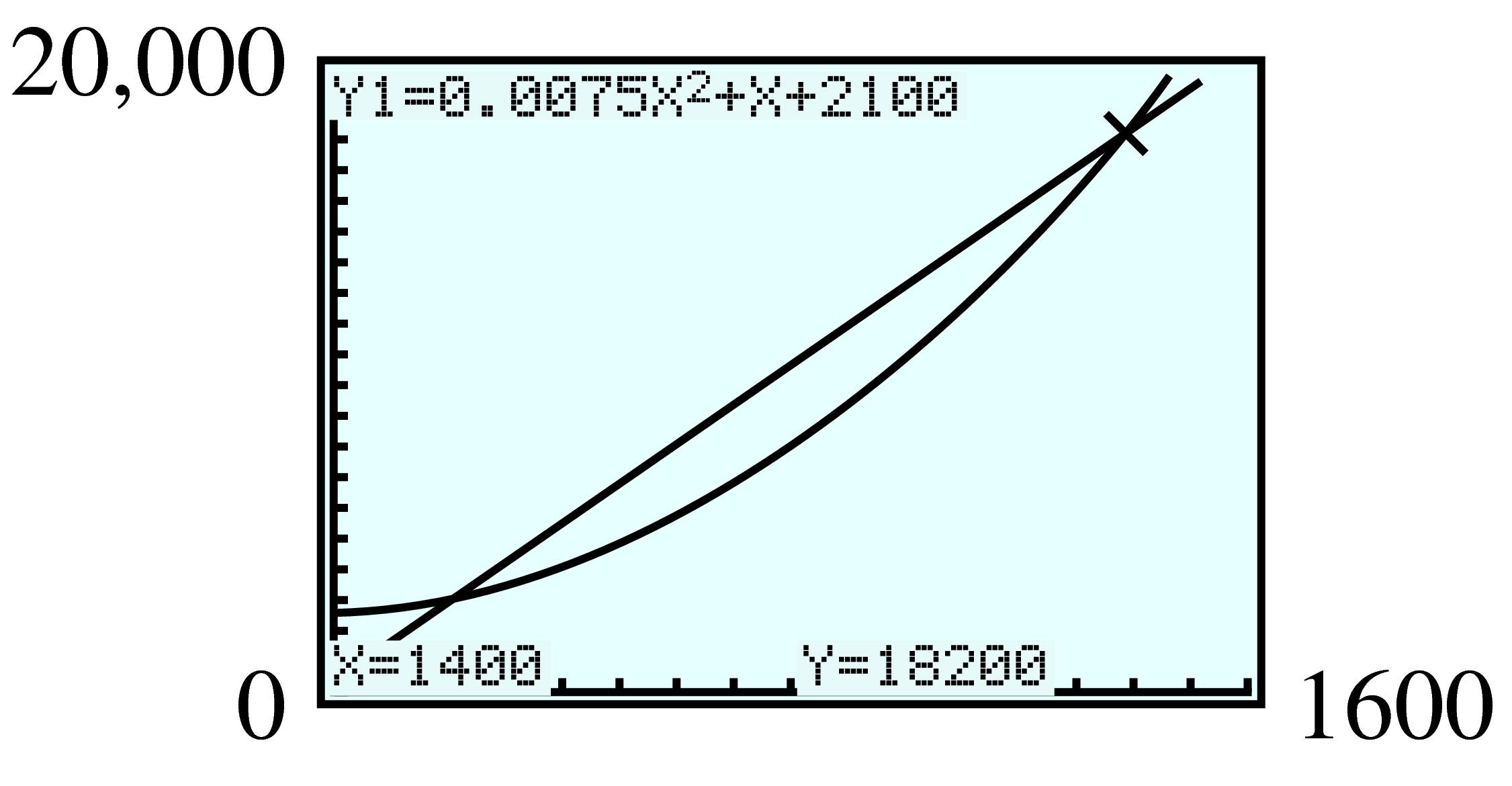
\(I=200+0.09 S\)

Skills Practice

1.1.3.5.
Answer.
\(\dfrac{6}{5} \)
1.1.3.7.
Answer.
\(y \gt \dfrac{6}{5} \)
1.1.3.9.
Answer.
\(R = 50- 0.4 w\)

Applications

1.1.3.11.
Answer.
  1. \(t\) (days) \(0\) \(5\) \(10\) \(15\) \(20\)
    \(h\) (inches) 6 16 26 36 46
  2. \(\displaystyle h=6+2t\)
  3. grid
  4. 48 in
  5. 33 days
  6. \(h=6+2(21)\text{;}\) \(72=6+2t\)
  7. 14 is the initial height of the plants in inches. 1.5 is the number of inches they grow each day.
1.1.3.13.
Answer.
  1. Altitude (1000 ft) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\)
    Boiling point (\(\degree\)F) \(212\) \(210\) \(208\) \(206\) \(204\) \(202\)
  2. boiling point
  3. \(4\degree\)F
  4. Over 4000 feet

1.2 Graphs and Equations
1.2.9 Problem Set 1.2

Warm Up

1.2.9.1.
Answer.
  1. no
  2. yes
  3. no
  4. no
1.2.9.3.
Answer.
  1. yes
  2. no
  3. no
  4. yes
1.2.9.5.
Answer.
  1. no
  2. no
  3. yes
  4. yes
1.2.9.7.
Answer.
horizontal: 0.25; vertical: 4
1.2.9.9.
Answer.
  1. horizontal: 5; vertical: 250
  2. points on grid

Skills Practice

1.2.9.11.
Answer.
\(\dfrac{-15}{4} \)
1.2.9.13.
Answer.
\(35\)
1.2.9.17.
Answer.
\(x\ge \dfrac{7}{2} \)
number line
1.2.9.19.
Answer.
\(y = \dfrac{2}{3} + 24\)
1.2.9.21.
Answer.
\(y = \dfrac{-7}{13}x + 7\)
1.2.9.23.
Answer.
\(y = \dfrac{2}{9}x + 17\)

Applications

1.2.9.25.
Answer.
    1. \(\displaystyle x = -6\)
    2. \(\displaystyle x\lt -6\)
    3. \(\displaystyle x\gt -6\)
    1. \(\displaystyle x = -6\)
    2. \(\displaystyle x\lt -6\)
    3. \(\displaystyle x\gt -6\)
1.2.9.27.
Answer.
  1. \(\displaystyle x=0.3\)
  2. \(\displaystyle x=0.8\)
  3. \(\displaystyle x \le 0.3\)
  4. \(\displaystyle x \ge 0.8\)
1.2.9.29.
Answer.
  1. \(\displaystyle x \le 4\)
  2. \(\displaystyle x \gt 2\)
1.2.9.31.
Answer.
  1. \(\displaystyle x=4\)
  2. \(\displaystyle x\lt 22\)
1.2.9.33.
Answer.
  1. \(\displaystyle p=120+5t\)
  2. increasing blood pressure
  3. 141
  4. 7.5 min

1.3 Intercepts
1.3.6 Problem Set 1.3

Warm Up

1.3.6.1.
Answer.
  1. \(\displaystyle 5x\)
  2. \(\displaystyle 2y\)
  3. 5x+2y=1000
1.3.6.3.
Answer.
\(y=\dfrac{-3}{5}x+\dfrac{16}{5} \)

Skills Practice

1.3.6.5.
Answer.
  1. \((4,0) \text{,}\) \((0,-3) \)
  2. line with positive intercepts
1.3.6.7.
Answer.
  1. \((-8,0) \text{,}\) \((0,5) \)
  2. line with positive intercepts
1.3.6.9.
Answer.
  1. \(\displaystyle (3,0), (0,5) \)
  2. \(\displaystyle \left(\dfrac{1}{2},0\right), \left(0,\dfrac{-1}{4}\right) \)
  3. \(\displaystyle \left(\dfrac{5}{2},0\right), \left(0,\dfrac{-3}{2}\right) \)
  4. \(\displaystyle (p,0), (0,q) \)
  5. The value of \(a\) is the \(x\)-intercept, and the value of \(b\) is the \(y\)-intercept.
1.3.6.11.
Answer.
  1. \(\displaystyle (0, b)\)
  2. \(\displaystyle \left(\dfrac{-b}{m},0\right)\)
1.3.6.13.
Answer.
\(-2x + 3y = 2400\)
1.3.6.15.
Answer.
\(3x + 400y = 240\)
1.3.6.17.
Answer.
  1. \(22x+9y=33\text{,}\) and
  2. \(\displaystyle y = \dfrac{11}{3} + \dfrac{-22}{9}x\)
1.3.6.19.
Answer.
  1. \(4x+12y=48\text{,}\) and
  2. \(\displaystyle y = 4 - \dfrac{1}{3}x\)

Applications

1.3.6.21.
Answer.
  1. \(\displaystyle 9x\)
  2. \(\displaystyle 4y\)
  3. \(\displaystyle 9x+4y=1800\)
  4. \((200,0) \) Delbert must eat 200g of figs daily if he eats no bananas.
  5. \((0,450) \) Delbert must eat 450g of bananas daily if he eats no figs.
1.3.6.23.
Answer.
  1. \(~ t ~\) \(0\) \(5\) \(10\) \(15\) \(20\)
    \(~ h ~\) \(-400\) \(-300\) \(-200\) \(-100\) \(0\)
  2. \(\displaystyle h=-44+20t \)
  3. grid
  4. \((0,-400) \text{:}\) The diver starts at a depth of 400 feet. \((20,0) \text{:}\) The diver surfaces after 20 minutes.
1.3.6.25.
Answer.
  1. $\(2.40x,\) $\(3.20y\)
  2. \(\displaystyle 2.40x + 3.20y = 19,200\)
  3. line
  4. The \(y\)-intercept, 6000 gallons, is the amount of premium that the gas station owner can buy if he buys no regular. The \(x\)-intercept, 8000 gallons, is the amount of regular he can buy if he buys no premium.

1.4 Slope
1.4.6 Problem Set 1.4

Warm Up

1.4.6.1.
Answer.
Anthony
1.4.6.3.
Answer.
Bob’s driveway
1.4.6.5.
Answer.
\(-1\)
1.4.6.7.
Answer.
\(\dfrac{-2}{3}\)

Skills Practice

1.4.6.9.
Answer.
  1. \(\displaystyle \dfrac{3}{2} \)
  2. \(\displaystyle 6,~ \dfrac{3}{2}\)
  3. \(\displaystyle -9,~ \dfrac{3}{2}\)
  4. 27
1.4.6.11.
Answer.
\(\dfrac{3}{4} \)
1.4.6.13.
Answer.
\(-4000\)
1.4.6.15.
Answer.
  1. 9x+12y=36
  2. \(\displaystyle m=\dfrac{-3}{4} \)
1.4.6.17.
Answer.
14.29 ft
1.4.6.19.
Answer.
(a)

Applications

1.4.6.21.
Answer.
  1. del x and del y
  2. 800
  3. \(\displaystyle P=7000+800t\)
1.4.6.23.
Answer.
  1. \(-6\) liters/day
  2. The water supply is decreasing at a rate of 6 liters per day.
  3. line with changes in W and t
  4. \(\displaystyle W=48-6t\)
1.4.6.25.
Answer.
  1. Yes, the slope is 0.12
  2. 0.12 cm/kg: The spring stretches an extra 0.12 cm for each additional 1 kg mass.
1.4.6.27.
Answer.
  1. The distances to the stations are known.
  2. 5.7 km/sec
1.4.6.29.
Answer.
  1. 7.9
  2. 8.35 km
  3. 2 hrs 5 min

1.5 Equations of Lines
1.5.7 Problem Set 1.5

Warm Up

1.5.7.1.
Answer.
\(x\) \(-1\) \(~0~\) \(~2~\) \(~3~\) \(~4~\)
\(y\) \(10\) \(8\) \(4\) \(2\) \(0\)
line
  1. 8
  2. decreases by 2 units
  3. The constant term is the \(y\)-intercept and the coefficient of \(x\) is the slope.
1.5.7.3.
Answer.
  1. \(\displaystyle \Delta h = 22\)
  2. \(\displaystyle \Delta r = -57\)

Skills Practice

1.5.7.5.
Answer.
  1. \(\displaystyle y=\dfrac{-3}{2}x+\dfrac{1}{2}\)
  2. \(\displaystyle m=\dfrac{-3}{2}; ~b=\dfrac{1}{2} \)
1.5.7.7.
Answer.
  1. \(\displaystyle y=14x-22\)
  2. \(\displaystyle m=14; ~b=-22 \)
1.5.7.9.
Answer.
  1. line
  2. \(\displaystyle y=\dfrac{-5}{3}x-6\)
  3. \(\displaystyle x=\dfrac{-18}{5}\)
1.5.7.11.
Answer.
  1. II
  2. III
  3. I
  4. IV
1.5.7.13.
Answer.
  1. line through (2,-5) with slope -3
  2. \(\displaystyle y+5 = -3(x-2) \)
  3. \(\displaystyle y=-3x+1\)
1.5.7.15.
Answer.
\(y=4x+40 \)
1.5.7.17.
Answer.
  1. III
  2. IV
  3. II
  4. I

Applications

1.5.7.19.
Answer.
  1. \(\displaystyle M = 7000 - 400w\)
  2. The slope tells us that Tammy’s bank account is diminishing at a rate of $400 per week, the vertical intercept that she had $7000 (when she lost all sources of income).
1.5.7.21.
Answer.
\(m = -0.0018\) degree/foot, so the boiling point drops with altitude at a rate of 0.0018 degree per foot. \(b = 212\text{,}\) so the boiling point is \(212\degree\) at sea level (where the elevation \(h = 0\)).
1.5.7.23.
Answer.
  1. \(h\) \(8\) \(20\)
    \(C\) \(645\) \(1425\)
  2. \(\displaystyle C=125+65h \)
  3. \(m =65 \text{,}\) the lesson rate is 65 dollars per hour
1.5.7.25.
Answer.
  1. \(C\) \(15\) \(-5\)
    \(F\) \(59\) \(23\)
  2. \(\displaystyle F=32+\dfrac{9}{5}C \)
  3. \(m =\dfrac{9}{5} \text{,}\) so an increase of \(1\degree\)C is equivalent to an increase of \(\dfrac{9}{5}\degree\)F.
1.5.7.27.
Answer.
  1. \(55\degree\)F
  2. 9840 ft
  3. temperature vs altitude
  4. \(m=\dfrac{-3}{820}\text{.}\) The temperature decreases 3 degrees for each increase in altitude of 820 feet.
  5. \((19,133 \frac{1}{3}, 0)\text{.}\) At an altitude of \(19,133 \frac{1}{3}\) feet, the temperature is \(0\degree\)F. \((0,70)\text{.}\) At an altitude of 0 feet, the temperature is \(70\degree\)F.
1.5.7.29.
Answer.
  1. \(\displaystyle (0,28) \)
    salt dissolved
  2. \(\displaystyle m=\dfrac{1}{2} \)
  3. \(\displaystyle y= \dfrac{1}{2}x + 28 \)
  4. \(\displaystyle 36\degree\text{C}\)

1.6 Chapter Summary and Review
1.6.3 Chapter 1 Review Problems

1.6.3.1.

Answer.
  1. \(n\) \(100\) \(500\) \(800\) \(1200\) \(1500\)
    \(C\) \(4000\) \(12,000\) \(18,000\) \(26,000\) \(32,000\)
  2. \(\displaystyle C = 20n + 2000\)
  3. cost of producing calculators
  4. $22,000
  5. 400

1.6.3.2.

Answer.
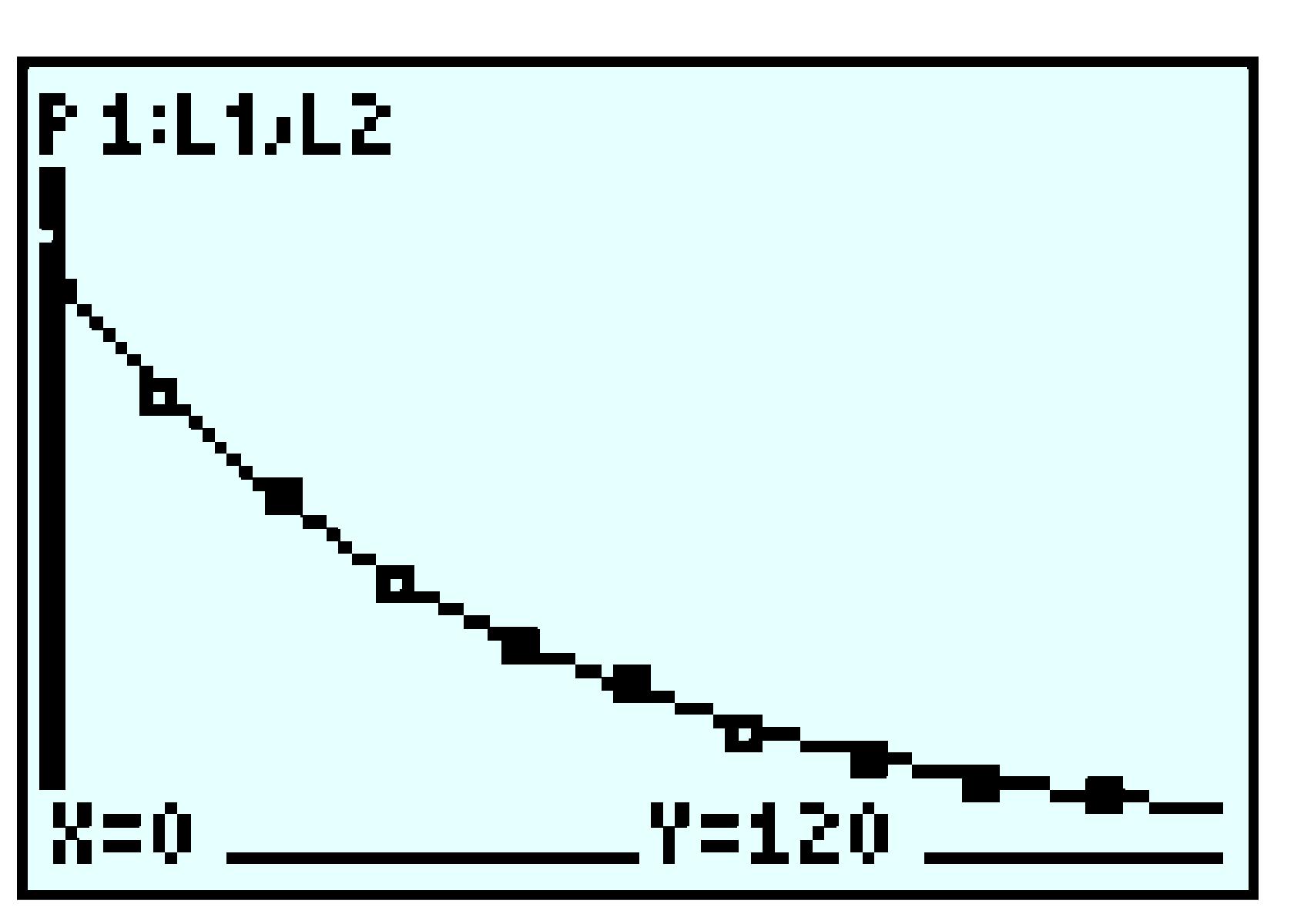
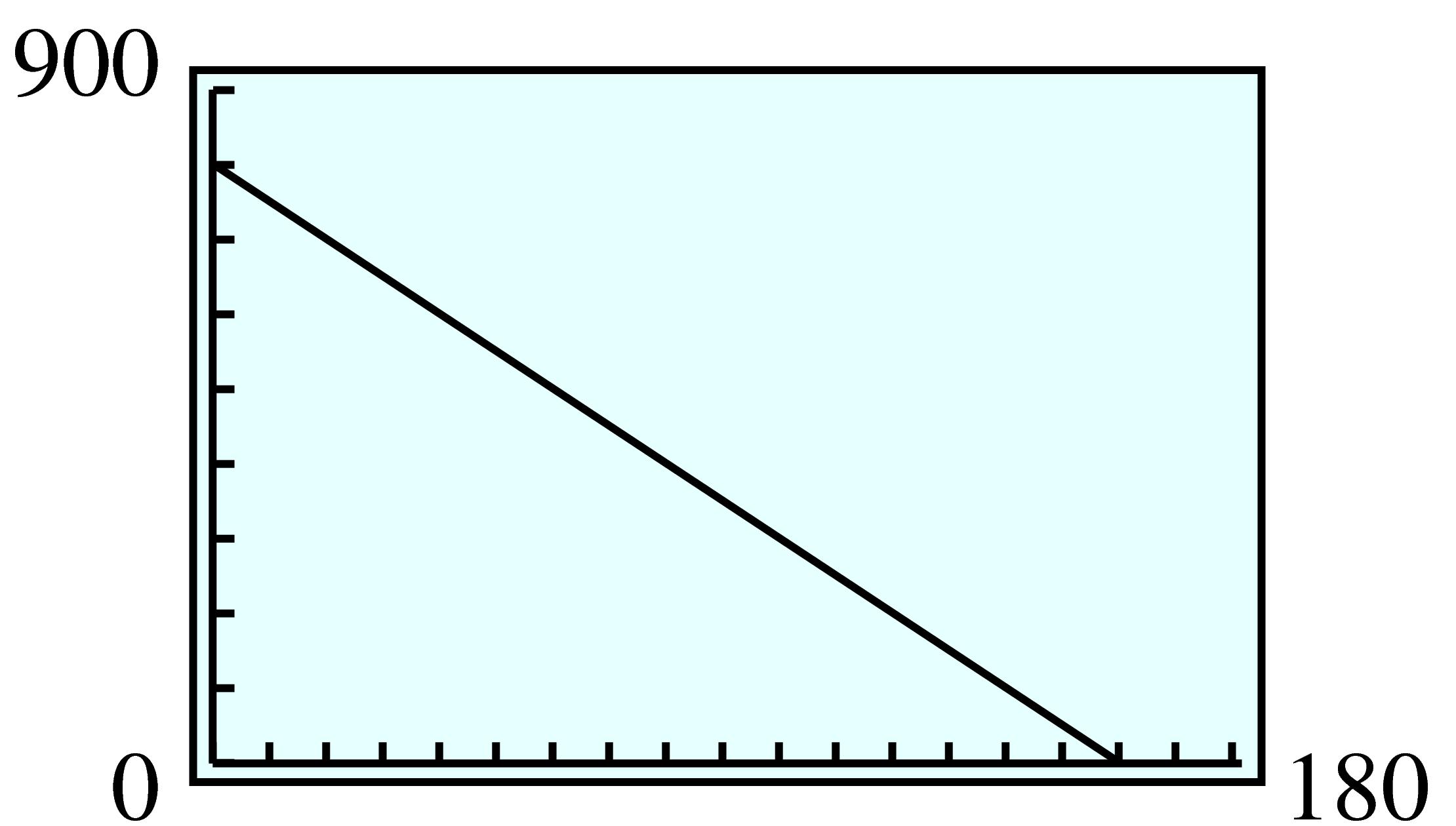
  1. \(t\) \(~ 5 ~\) \(~10~\) \(~15~\) \(~20~\) \(~25~\)
    \(R\) \(1960\) \(1820\) \(1680\) \(1540\) \(1400\)
  2. \(\displaystyle R = 2100 - 28t\)
  3. \((75, 0)\text{,}\) \((0, 2100)\)
    grid
  4. \(t\)-intercept: The oil reserves will be gone in 2080; \(R\)-intercept: There were \(2100\) billion barrels of oil reserves in 2005.

1.6.3.3.

Answer.
  1. \(\displaystyle 60C+100T=1200\)
  2. \((20,0) \text{,}\) \((0,12) \)
    grid
  3. 6 days
  4. She can spend 20 days in Atlantic City if she spends no time in Saint-Tropez, or 12 days in Saint-Tropez if she spends no time in Atlantic City.

1.6.3.4.

Answer.
line with x-intercept 5, y-intercept -12

1.6.3.5.

Answer.
line with x-intercept -400, y-intercept 500

1.6.3.6.

Answer.
line with x-intercept 6, y-intercept 4

1.6.3.7.

Answer.
line through origin with slope 3/4

1.6.3.8.

Answer.
line through origin with slope -1/4

1.6.3.9.

Answer.
verticalline x= -3

1.6.3.10.

Answer.
  1. \(\displaystyle B = 800 - 5t\)
  2. GC graph
  3. \(m = -5\) thousand barrels/minute: The amount of oil in the tanker is decreasing by 5000 barrels per minute.

1.6.3.11.

Answer.
  1. \(\displaystyle F = 500 + 0.10C\)
  2. GC graph
  3. \(m = 0.10\text{:}\) The fee increases by $0.10 for each dollar increase in the remodeling job.

1.6.3.12.

Answer.
\(\dfrac{-3}{2} \)

1.6.3.13.

Answer.
\(2 \)

1.6.3.14.

Answer.
\(-0.4 \)

1.6.3.15.

Answer.
\(-1.75\)

1.6.3.16.

Answer.
neither

1.6.3.17.

Answer.
both

1.6.3.18.

Answer.
\(d\) \(V\)
\(-5\) \(-4.8\)
\(-2\) \(-3 \)
\(1\) \(-1.2\)
\(6\) \(1.8 \)
\(10\) \(4.2\)

1.6.3.19.

Answer.
\(q\) \(S\)
\(-8\) \(-8\)
\(-4\) \(36 \)
\(3\) \(168\)
\(5\) \(200 \)
\(9\) \(264\)

1.6.3.20.

Answer.
80 ft

1.6.3.21.

Answer.
\(m=\dfrac{1}{2} \text{,}\) \(b= \dfrac{-5}{4} \)

1.6.3.22.

Answer.
\(m=\dfrac{3}{4} \text{,}\) \(b= \dfrac{5}{4} \)

1.6.3.23.

Answer.
\(m=-4 \text{,}\) \(b= 3 \)

1.6.3.24.

Answer.
\(m=0 \text{,}\) \(b= 3 \)

1.6.3.25.

Answer.
  1. line through (-4,6), slope -2/3
  2. \(\displaystyle y=\dfrac{-2}{3}x +\dfrac{10}{3} \)

1.6.3.26.

Answer.
  1. line through (2,-5), slope 3/2
  2. \(\displaystyle y=\dfrac{3}{2}x -8 \)

1.6.3.27.

Answer.
  1. \(\displaystyle T = 62 - 0.0036h\)
  2. \(-46\degree\text{F}\text{;}\) \(108\degree\text{F}\)
  3. \(\displaystyle -71\degree\text{F}\)

1.6.3.28.

Answer.
\(y=\dfrac{-9}{5}x+\dfrac{2}{5} \)

1.6.3.29.

Answer.
\(y=\dfrac{-5}{2}x+8 \)

1.6.3.30.

Answer.
  1. \(t\) \(0\) \(15\)
    \(P\) \(4800\) \(6780\)
  2. \(\displaystyle P = 4800 + 132t\)
  3. \(m = 132\) people/year: the population grew at a rate of \(132\) people per year.

1.6.3.31.

Answer.
  1. \(m=-2\text{;}\) \(b=3\)
  2. \(\displaystyle y=-2x+3\)

1.6.3.32.

Answer.
  1. \(m=\dfrac{3}{2} \text{;}\) \(b=-5\)
  2. \(\displaystyle y=\dfrac{3}{2}x-5\)

1.6.3.33.

Answer.
\(\dfrac{3}{5} \)

1.6.3.34.

Answer.
  1. \((4,0) \) and \((0,-6) \)
  2. \(\displaystyle \dfrac{3}{2} \)

1.6.3.35.

Answer.
  1. \(\left(\dfrac{8}{3},0 \right) \) and \((0,-4) \)
  2. \((4,3) \text{;}\) No

2 Applications of Linear Models
2.1 Linear Regression
2.1.5 Problem Set 2.1

Warm Up

2.1.5.1.
Answer.
a: II; b: III; c: I; d: IV
2.1.5.2.
Answer.
a: III; b: IV; c: II; d: I
2.1.5.3.
Answer.
  1. \(k\) \(70\) \(50\)
    \(p\) \(154\) \(110\)
  2. \(\displaystyle p=2.2k \)
  3. \(m =2.2 \) pounds/kg is the conversion factor from kilograms to pounds

Skills Practice

2.1.5.5.
Answer.
The slope is \(-2.5\text{,}\) which indicates that the snack bar sells 2.5 fewer cups of cocoa for each \(1\degree\text{C}\) increase in temperature. The \(C\)-intercept of 52 indicates that 52 cups of cocoa would be sold at a temperature of \(0\degree\text{C}\text{.}\) The \(T\)-intercept of 20.8 indicates that no cocoa will be sold at a temperature of \(20.8\degree\text{C}\text{.}\)
2.1.5.7.
Answer.
scatterplot and line
2.1.5.9.
Answer.
  1. 74 feet
  2. The young whale grows in length about 4.14 foot per month
2.1.5.11.
Answer.
2 min: \(21\degree\)C; 2 hr: \(729\degree\)C; The estimate at 2 minutes is reasonable; the estimate at 2 hours is not reasonable.

Applications

2.1.5.13.
Answer.
  1. 12 seconds
  2. 39
  3. scatterplot with regression line
  4. 11.6 seconds
  5. \(\displaystyle y = 8.5 + 0.1x\)
  6. 12.7 seconds; 10.18 seconds; The prediction for the 40-year-old is reasonable, but not the prediction for the 12-year-old.
2.1.5.15.
Answer.
  1. graph
  2. 53 sec, 64 sec
  3. \(\displaystyle y=5.5x-8.6\)
  4. 57.95 sec
2.1.5.17.
Answer.
  1. scatterplot with regression line
  2. \(\displaystyle y = 121 + 19.86t\)
  3. \(\displaystyle 419 \)
2.1.5.19.
Answer.
  1. scatterplot and regression line
  2. The graph is above.
  3. The slope tells us that the time it takes for a bird to attract a mate decreases by 0.85 days for every additional song it learns.
  4. 44.5 days
  5. The \(C\)-intercept tells us that a warbler with a repretoire of 53 songs would acquire a mate immediately. The \(B\)-intercept tells us that a warbler with no songs would take 62 days to find a mate. These values make sense in context.

2.2 Linear Systems
2.2.6 Problem Set 2.2

Warm Up

2.2.6.1.
Answer.
line
2.2.6.3.
Answer.
18.75

Skills Practice

2.2.6.5.
Answer.
\((-4,5)\)
2.2.6.7.
Answer.
\((-2,3) \)
2.2.6.9.
Answer.
Inconsistent
2.2.6.11.
Answer.
Dependent

Applications

2.2.6.13.
Answer.
  1. Sporthaus: \(y=500+10x\)
    Fitness First: \(y=50+25x\)
  2. \(x\) Sporthaus Fitness First
    6 560 200
    12 620 350
    18 680 500
    24 740 650
    30 800 800
    36 860 950
    42 920 1100
    48 980 1250
  3. Cost for fitness clubs
  4. 30 months
2.2.6.15.
Answer.
  1. \(\displaystyle 10x + 5y = 300\)
  2. \(\displaystyle y=3x\)
  3. two lines
    \(\displaystyle (12,36) \)
  4. She should buy 12 hardbacks and 36 paperbacks.
2.2.6.17.
Answer.
  1. \(\displaystyle S=1.5x\)
  2. \(\displaystyle D=120-2.5x\)
  3. two lines
  4. \(x=30\text{;}\) \(S=45\)
2.2.6.19.
Answer.
  1. The median age
  2. grid
  3. 0.3 years of age per year since 1990
  4. See (b) above
  5. Slightly less than 14 years since 1990
  6. More than half the women are older than the mean age of women.

2.3 Algebraic Solution of Systems
2.3.4 Problem Set 2.3

Warm Up

2.3.4.1.
Answer.
\((4,1) \)

Skills Practice

2.3.4.3.
Answer.
\((1,2) \)
2.3.4.7.
Answer.
\((1,2) \)
2.3.4.9.
Answer.
Dependent

Applications

2.3.4.11.
Answer.
  1. \(\displaystyle S=2.5x;~~D=350-4.5x\)
  2. 50 dollars per machine; 125 machines
2.3.4.13.
Answer.
  1. Pounds % silver Amount of silver
    First alloy \(x\) \(0.45\) \(0.45x\)
    Second alloy \(y\) \(0.60\) \(0.60y\)
    Mixture \(40\) \(0.48\) \(0.48(40)\)
  2. \(\displaystyle x+y=40\)
  3. \(\displaystyle 0.45x+0.60y=19.2 \)
  4. 32 lb
2.3.4.15.
Answer.
  1. Rani’s speed in still water: \(x\)
    Speed of the current: \(y\)
    Rate Time Distance
    Downstream \(x+y\) \(45\) \(6000\)
    Upstream \(x-y\) \(45\) \(4800\)
  2. \(\displaystyle 45(x+y)=6000 \)
  3. \(\displaystyle 45(x-y)=4800 \)
  4. Rani’s speed in still water is 120 meters per minute, and the speed of the current is \(13\dfrac{1}{3} \) meters per minute.
2.3.4.17.
Answer.
607.5 mi
2.3.4.19.
Answer.
  1. Sports coupes Wagons Total
    Hours of riveting 3 4 120
    Hours of welding 4 5 155
  2. \(\displaystyle 3x+4y=120\)
  3. \(\displaystyle 4x+5y=155\)
  4. 20 sports coupes and 15 wagons

2.4 Gaussian Reduction
2.4.6 Problem Set 2.4

Warm Up

2.4.6.1.
Answer.
\((-3,-5) \)
2.4.6.3.
Answer.
  1. Principal Interest rate Interest
    Bonds \(x\) \(0.10\) \(0.10x\)
    Certificate \(y\) \(0.08\) \(0.08y\)
    Total \(2000\) —— \(184\)
  2. \(\displaystyle x+y=2000\)
  3. \(\displaystyle 0.10x+0.08y=184\)

Skills Practice

2.4.6.5.
Answer.
\((-2,0,3) \)
2.4.6.7.
Answer.
\((2,-2,0) \)
2.4.6.9.
Answer.
\((2,-3,1) \)
2.4.6.11.
Answer.
\(\left(\dfrac{1}{2}, \dfrac{2}{3},-3 \right) \)
2.4.6.13.
Answer.
\(\left(\dfrac{1}{2}, -\dfrac{1}{2},\dfrac{1}{3} \right) \)
2.4.6.15.
Answer.
Dependent

Applications

2.4.6.17.
Answer.
\(x=40\) in, \(y=60\) in, \(z=55\) in
2.4.6.19.
Answer.
\(\dfrac{1}{2} \) lb Colombian, \(\dfrac{1}{4} \) lb French, \(\dfrac{1}{4} \) Sumatran

2.5 Linear Inequalities in Two Variables
2.5.5 Problem Set 2.5

Warm Up

2.5.5.1.
Answer.
  1. \(x\) \(-2\) \(5\) \(6\) \(8\)
    \(y\) \(12\) \(5\) \(4\) \(2\)
  2. grid
  3. \(\displaystyle x+y=10\)
  4. See above.
2.5.5.3.
Answer.
  1. The graph of the equation is a line, and the graph of the inequality is a half-plane. The line is the boundary of the half-plane but is not included in the solution to the inequality.
  2. The graph of \(x + y\ge 10,000\) includes both the line \(x + y=10,000\) and the half-plane of the corresponding strict inequality.

Skills Practice

2.5.5.5.
Answer.
linear inequality in two variables
2.5.5.7.
Answer.
linear inequality in two variables
2.5.5.9.
Answer.
linear inequality in two variables
2.5.5.11.
Answer.
linear inequality in two variables
2.5.5.13.
Answer.
linear inequality in two variables
2.5.5.14.
Answer.
linear inequality in two variables
2.5.5.15.
Answer.
system of inequalities
2.5.5.17.
Answer.
system of inequalities, with vertices
2.5.5.19.
Answer.
system of inequalities
2.5.5.21.
Answer.
system of inequalities, with vertices
2.5.5.23.
Answer.
system of inequalities, with vertices

Applications

2.5.5.25.
Answer.
system of inequalities
2.5.5.27.
Answer.
graph

2.6 Chapter Summary and Review
2.6.3 Chapter 2 Review Problems

2.6.3.1.

Answer.
  1. regression line for boiling point vs heat of vaporization
  2. 235 kilojoules
  3. \(\displaystyle y=0.106x + 4.6\)
  4. \(\displaystyle 156.7\degree\text{C}\)

2.6.3.2.

Answer.
scatterplot with regression line
  1. \(45\) cm
  2. \(87\) cm
  3. \(\displaystyle y = 1.2x - 3\)
  4. \(69\) cm
  5. \(y = 1.197x - 3.660\text{;}\) \(68.16\) cm

2.6.3.3.

Answer.
6

2.6.3.4.

Answer.
26 min

2.6.3.5.

Answer.
\((-1,2) \)

2.6.3.6.

Answer.
\((1.9, -0.8) \)

2.6.3.7.

Answer.
\(\left(\dfrac{1}{2}, \dfrac{7}{2} \right) \)

2.6.3.8.

Answer.
\((1,2) \)

2.6.3.9.

Answer.
\((1,2) \)

2.6.3.10.

Answer.
\(\left(\dfrac{1}{2}, \dfrac{3}{2} \right)\)

2.6.3.11.

Answer.
Consistent and independent

2.6.3.12.

Answer.
Inconsistent

2.6.3.13.

Answer.
Dependent

2.6.3.14.

Answer.
Consistent and independent

2.6.3.15.

Answer.
\((2,0,-1) \)

2.6.3.16.

Answer.
\((2,1,-1) \)

2.6.3.17.

Answer.
\((2,-5,3) \)

2.6.3.18.

Answer.
\(\left(2,\dfrac{3}{2},-1\right) \)

2.6.3.19.

Answer.
\((-2,1,3) \)

2.6.3.20.

Answer.
\((2,-1,0) \)

2.6.3.21.

Answer.
26

2.6.3.22.

Answer.
17

2.6.3.23.

Answer.
$3181.82 at 8%, $1818.18 at 13.5%

2.6.3.24.

Answer.
$4000

2.6.3.25.

Answer.
5 cm, 12 cm, 13 cm

2.6.3.26.

Answer.
20 to Boston, 25 to Chicago, 10 to Los Angeles

2.6.3.27.

Answer.
strict inequality

2.6.3.28.

Answer.
strict inequality

2.6.3.29.

Answer.
strict inequality

2.6.3.30.

Answer.
compound inequality

2.6.3.31.

Answer.
system of inequalities

2.6.3.32.

Answer.
system of inequalities

2.6.3.33.

Answer.
system of inequalities

2.6.3.34.

Answer.
system of inequalities

2.6.3.35.

Answer.
system of inequalities

2.6.3.36.

Answer.
system of inequalities

2.6.3.37.

Answer.
system of inequalities

2.6.3.38.

Answer.
system of inequalities

2.6.3.39.

Answer.
\(20p+9g \le 120\text{,}\) \(10p+10g \le 120\text{,}\) \(p\ge 0\text{,}\) \(g\ge 0\)
system of inequalities

2.6.3.40.

Answer.
\(x+y \le 32\text{,}\) \(2x+1.6y \ge 56\text{,}\) \(x\ge 0\text{,}\) \(y\ge 0\text{,}\) where \(x\) represents ounces of tofu, \(y\) the ounces of tempeh
system of inequalities

3 Quadratic Models
3.1 Extraction of Roots
3.1.8 Problem Set 3.1

Warm Up

3.1.8.1.
Answer.
  1. \(\displaystyle -12\)
  2. \(\displaystyle -2\)
  3. \(\displaystyle 9\)
3.1.8.3.
Answer.
  1. \(\displaystyle 29\)
  2. \(\displaystyle 7\)
  3. \(\displaystyle \sqrt{6}\)
3.1.8.4.
Answer.
  1. \(\displaystyle \pm 7\)
  2. \(\displaystyle \pm \dfrac{5}{2}\)
  3. \(\displaystyle \pm \sqrt{5}\)
3.1.8.5.
Answer.
  1. parabola
  2. Two solutions. \(\approx \pm 2.5\)
  3. \(\displaystyle \pm \sqrt{6}\)

Skills Practice

3.1.8.7.
Answer.
\(\pm \sqrt{3}\)
3.1.8.9.
Answer.
\(\dfrac{5}{2},~\dfrac{-3}{2} \)
3.1.8.11.
Answer.
\(\dfrac{2}{3} \pm \dfrac{\sqrt{5}}{3}\)
3.1.8.13.
Answer.
\(\dfrac{7}{8},\pm \dfrac{\sqrt{8}}{8} \)
3.1.8.15.
Answer.
\(\pm 5.73\)
3.1.8.17.
Answer.
b. 10, -2
3.1.8.19.
Answer.
\(\pm \dfrac{Fr}{m}\)
3.1.8.21.
Answer.
\(\pm pi \sqrt{\dfrac{L}{8}}\)

Applications

3.1.8.23.
Answer.
21 in
3.1.8.25.
Answer.
  1. \(\displaystyle A=1600(1+r)^2\)
  2. \(~r~\) \(0.02\) \(0.04\) \(0.06\) \(0.08\)
    \(~A~\) \(1664.64\) \(1730.56\) \(1797.76\) \(1866.24\)
  3. 11.8%
3.1.8.27.
Answer.
19 ft by 57 ft
3.1.8.29.
Answer.
  1. \(\displaystyle V=62.8r^2\)
  2. \(\displaystyle \dfrac{1}{4}\)
  3. 1.96 cm
3.1.8.31.
Answer.
  1. \(\displaystyle \pm \sqrt{\dfrac{bc}{a}}\)
  2. \(\displaystyle \pm \sqrt{\dfrac{ac}{b}}\)

3.2 Intercepts, Solutions, and Factors
3.2.6 Problem Set 3.2

Warm Up

3.2.6.1.
Answer.
  1. \(\displaystyle 2b^2+9b-18\)
  2. \(\displaystyle 12z^2-35z+8\)
3.2.6.3.
Answer.
  1. \(\displaystyle 6p^3-33p^2+45p\)
  2. \(\displaystyle 6v^3+16v^2-32v\)
3.2.6.5.
Answer.
  1. \(\displaystyle (x-4)(x+4)\)
  2. \(\displaystyle x(x-16)\)
  3. \(\displaystyle (x-4)(x-4)\)
  4. cannot be factored
3.2.6.7.
Answer.
\((x-5)(x-2)\)
3.2.6.9.
Answer.
\((w-8)(w+4)\)
3.2.6.11.
Answer.
\((x-5)(x-2)\)

Skills Practice

3.2.6.13.
Answer.
\(\dfrac{1}{2}, ~-3\)
3.2.6.15.
Answer.
\(0,~3\)
3.2.6.17.
Answer.
\(\dfrac{1}{2}, ~1\)
3.2.6.19.
Answer.
\(-1,2\)
3.2.6.21.
Answer.
\(\dfrac{7}{8} \pm \dfrac{\sqrt{5}}{8}\)
3.2.6.23.
Answer.
\(\dfrac{b \pm 5}{a}\)
3.2.6.25.
Answer.
\(0.1(x-18)(x+15)\)
3.2.6.27.
Answer.
All three graphs have the same \(x\)-intercepts.

Applications

3.2.6.29.
Answer.
c. 306.5 ft at 0.625 sec d. 1.25 sec e. 5 sec
3.2.6.31.
Answer.
b. \(h^2+10^2=(h+2)^2\) c. 24 ft
3.2.6.33.
Answer.
  1. \(\displaystyle l=x-4,~w=x-4,~h=2,~V=2(x-4)^2\)
  2. 0 cubic in, 2 cubic in, 8 cubic in, etc.
  3. \(\displaystyle x = 4\)
  4. 9 in by 9 in
  5. \(\displaystyle 2(x-4)^2 = 50;~ x=9\)
3.2.6.34.
Answer.
a. \(l=6, ~w=1-2x, ~h=x, ~V=6x(1-2x)~~\) e. \(6x(1-2x)=\dfrac{3}{4};~~\dfrac{1}{4}~\) ft

3.3 Graphing Parabolas
3.3.6 Problem Set 3.3

Warm Up

3.3.6.1.
Answer.
\(13\)
3.3.6.4.
Answer.
  1. factoring; \(0,10\)
  2. extraction of roots; \(\pm \sqrt{10}\)
  3. factoring; \(\dfrac{-1}{2}, 1\)
  4. extraction of roots; \(\dfrac{-5}{2}, \dfrac{-5}{2}\)
3.3.6.6.
Answer.
\(2 \pi R(R+H)\)
3.3.6.8.
Answer.
\(0, -35\)

Skills Practice

3.3.6.9.
Answer.
  1. ii
  2. iv
  3. i
  4. iii
  5. vi
  6. v
3.3.6.11.
Answer.
    1. Narrower
    2. graph y=2x-squared
    1. Wider
    2. graph y=2x-squared
    1. Opens downward
    2. graph y=neg x-squared
3.3.6.13.
Answer.
\((0,0), (4,0); (2,-4)\)
parabola
3.3.6.15.
Answer.
\((0,0), (-2,0); (-1,-3)\)
parabola
3.3.6.17.
Answer.
\((0,0), (20,0); (10,200)\)
parabola

Applications

3.3.6.19.
Answer.
  1. \(\displaystyle (2000, 400)\)
  2. \(\displaystyle (0,0), (4000,0)\)
  3. parabola
  4. \(\displaystyle x \gt 4000\)
3.3.6.21.
Answer.
  1. basic parabola
  2. narrower
  3. wider
  4. narrower and reflected about \(y\)-axis
3.3.6.23.
Answer.
  1. \(x\)-intercepts at 0 and 4
  2. \(x\)-intercepts at 0 and \(-4\)
  3. reflection of (a) about \(y\)-axis
  4. reflection of (b) about \(y\)-axis

3.4 Completing the Square
3.4.4 Problem Set 3.4

Warm Up

3.4.4.1.
Answer.
\(-4, \dfrac{5}{2}\)
3.4.4.3.
Answer.
  1. \(\displaystyle x^2+10x+25\)
  2. \(\displaystyle x^2-12x+36\)
  3. \(\displaystyle x^2-24x+144\)
  4. \(\displaystyle x^2+30x+225\)

Skills Practice

3.4.4.5.
Answer.
b and c
3.4.4.7.
Answer.
\(-4, -5\)
3.4.4.9.
Answer.
\(-1 \pm \sqrt{\dfrac{5}{2}}\)
3.4.4.11.
Answer.
\(\dfrac{-5}{2} \pm \sqrt{\dfrac{45}{4}}\)
3.4.4.13.
Answer.
\(-5,8\)
3.4.4.15.
Answer.
\(-3, \dfrac{4}{3}\)

Applications

3.4.4.17.
Answer.
  1. \(\displaystyle (\dfrac{1}{4} \pm \sqrt{\dfrac{13}{15}}, 0)\)
  2. \(\displaystyle (\dfrac{1}{4}, -3\dfrac{1}{4})\)
3.4.4.19.
Answer.
  1. \(\displaystyle (-2,0),~(\dfrac{2}{5},0)\)
  2. \(\displaystyle (\dfrac{-4}{5}, -7\dfrac{1}{5})\)
3.4.4.21.
Answer.
  1. \(\displaystyle L^2+(L-4)^2=20^2\)
  2. 12 in by 16 in
3.4.4.23.
Answer.
  1. \(\displaystyle A = \dfrac{1}{2}(x^2-y^2)\)
  2. \(\displaystyle A = \dfrac{1}{2}(x-y)(x+y)\)
  3. 18 sq ft
3.4.4.25.
Answer.
  1. \(\displaystyle A = (x+y)^2\)
  2. \(\displaystyle A = x^2+2xy+y^2\)
  3. graph
3.4.4.27.
Answer.
\(-1 \pm \sqrt{1-c}\)
3.4.4.29.
Answer.
\(\dfrac{b}{2} \pm \dfrac{b^2-4c}{4}\)
3.4.4.31.
Answer.
\(\pm \sqrt{\dfrac{V}{2w} - s^2}\)
3.4.4.33.
Answer.
\((-15,0), (15,0); (0,255)\)
3.4.4.35.
Answer.
\(\dfrac{-3x \pm 3}{2}\)

3.5 Chapter 3 Summary and Review
3.5.3 Chapter 3 Review Problems

3.5.3.1.

Answer.
\(\pm \sqrt{2}\)

3.5.3.2.

Answer.
\(\pm \sqrt{40}\)

3.5.3.3.

Answer.
\(-4 \pm \sqrt{20}\)

3.5.3.4.

Answer.
\(\dfrac{1 \pm \sqrt{15}}{7}\)

3.5.3.5.

Answer.
\(1,~4\)

3.5.3.6.

Answer.
\(11.5,~23.5\)

3.5.3.7.

Answer.
\(\dfrac{-3}{2},~2\)

3.5.3.8.

Answer.
\(2,~2\)

3.5.3.9.

Answer.
\(-2,~3\)

3.5.3.10.

Answer.
\(-1,~1\)

3.5.3.11.

Answer.
\(4x^2-29x-24=0\)

3.5.3.12.

Answer.
\(9x^2-30x+25=0\)

3.5.3.13.

Answer.
\(y=(x-3)(x+2.4)\)

3.5.3.14.

Answer.
\(y=-(x+1.3)(x-2)\)

3.5.3.15.

Answer.
  1. Vertex: \((0,0)\text{,}\) \(y\)-int: \((0,0)\text{,}\) \(x\)-int: \((0,0)\)
  2. parabola

3.5.3.17.

Answer.
  1. Vertex: \(\left(\dfrac{9}{2},\dfrac{-81}{4}\right)\text{,}\) \(y\)-int: \((0,0)\text{,}\) \(x\)-int: \((0,0),~(9,0)\)
  2. parabola

3.5.3.19.

Answer.
\(2 \pm \sqrt{10}\)

3.5.3.20.

Answer.
\(\dfrac{-3}{2} \pm \sqrt{\dfrac{21}{4}}\)

3.5.3.21.

Answer.
\(\dfrac{3}{2} \pm \sqrt{\dfrac{3}{4}}\)

3.5.3.22.

Answer.
\(\dfrac{1}{3} \pm \sqrt{\dfrac{10}{9}}\)

3.5.3.23.

Answer.
\(v=\pm \sqrt{\dfrac{2K}{m}}\)

3.5.3.24.

Answer.
\(b=\pm \sqrt{c^2-a^2}\)

3.5.3.25.

Answer.
\(s=\pm \sqrt{\dfrac{3V}{h}}\)

3.5.3.26.

Answer.
\(r=\pm \sqrt{\dfrac{A}{P}}-1\)

3.5.3.27.

Answer.
9

3.5.3.28.

Answer.
13

3.5.3.29.

Answer.
11%

3.5.3.30.

Answer.
8.5%

3.5.3.31.

Answer.
\(\sqrt{108} \approx 10.4\) in

3.5.3.32.

Answer.
17 in

3.5.3.33.

Answer.
1 sec

3.5.3.34.

Answer.
50 ft by 150 ft

3.5.3.35.

Answer.
\(A_1=x^2-\left(\dfrac{1}{2}y^2+\dfrac{1}{2}y^2\right)=x^2-y^2;~~A_2=(x+y)(x-y)=x^2-y^2\)

3.5.3.36.

Answer.
\(A_1=\pi (x+y)^2- \pi x^2 - \pi y^2 = 2 \pi xy;~~A_2=\pi y (2x) = 2 \pi xy\)

4 Applications of Quadratic Models
4.1 Quadratic Formula
4.1.6 Problem Set 4.1

Warm Up

4.1.6.1.
Answer.
  1. \(\displaystyle 8-2\sqrt{20}\)
  2. \(\displaystyle 9\)
4.1.6.3.
Answer.
  1. \(\displaystyle A=lw,~P=2l+2w\)
    1. \(A=24\) sq ft, \(P=20\) ft
    2. \(A=24\) sq ft, \(P=22\) ft

Skills Practice

4.1.6.5.
Answer.
0.618, -1.618
4.1.6.7.
Answer.
0.232, 1.434
4.1.6.9.
Answer.
1.270, 2.480
4.1.6.11.
Answer.
  1. graph
  2. Approximately \((1.5,0)\) and \((-0.3,0)\)
  3. \(\dfrac{3}{2}\) and \(\dfrac{-1}{3}\text{.}\) These are the \(x\)-intercepts of the graph.
4.1.6.13.
Answer.
  1. \((5,0)\) and \((1,0)\text{;}\) \((3,0)\text{;}\) no \(x\)-intercepts
  2. 1 and 5; 3; \(\dfrac{6 \pm i\sqrt{12}}{2}\text{.}\) The real-valued solutions are the \(x\)-intercepts of the graph. If the solutions are complex, the graph has no \(x\)-intercepts.
4.1.6.15.
Answer.
  1. \(\displaystyle x^2-4x-1=0\)
  2. \(\displaystyle x^2-8x+25=0\)
4.1.6.17.
Answer.
\(\dfrac{-4 \pm \sqrt{16-64h}}{32}\)
4.1.6.19.
Answer.
\(\dfrac{v \pm \sqrt{v^2-2as}}{a}\)
4.1.6.21.
Answer.
\(\dfrac{-1 \pm \sqrt{1+8S}}{2}\)

Applications

4.1.6.23.
Answer.
c. 31.77 mph
4.1.6.25.
Answer.
  1. 357 km
  2. 7100 m
4.1.6.27.
Answer.
b. \(10h(2h-6)=2160~~~\)c. 12 ft by 18 ft by 10ft

4.2 The Vertex
4.2.5 Problem Set 4.2

Warm Up

4.2.5.1.
Answer.
  1. \(t\) \(0\) \(0.25\) \(0.5\) \(0.75\) \(1\) \(0.25\) \(1.5\)
    \(h\) \(-12\) \(-5\) \(0\) \(3\) \(4\) \(3\) \(0\)
  2. grid
  3. \(\displaystyle (1,4)\)
  4. The wrench reaches its greatest height of 4 feet.
  5. The wrench reaches its greatest height 1 second after Francine throws it.
4.2.5.3.
Answer.
  1. \(\displaystyle y = x^2-3x-4\)
  2. y = -x^2+3x+4

Skills Practice

4.2.5.5.
Answer.
\((-2,3) \)
parabola
4.2.5.7.
Answer.
  1. \(\displaystyle (3,0)\)
  2. \(\displaystyle (3,0)\)
  3. \(\displaystyle (3,4)\)
4.2.5.9.
Answer.
  1. \(\displaystyle (3,4)\)
  2. parabola
  3. \(\displaystyle y=2x^2-12x+22\)
4.2.5.11.
Answer.
  1. \(\displaystyle y=a(x+2)^2+6\)
  2. 3
4.2.5.13.
Answer.
\(y=(3x+1)^2-5\)
4.2.5.15.
Answer.
  1. IV
  2. V
  3. I
  4. VII

Applications

4.2.5.17.
Answer.
  1. \(\displaystyle l=40-w;~A=40w-w^2\)
  2. 400 sq yd; 20 yd by 20 yd
4.2.5.19.
Answer.
  1. (table)
  2. \(\displaystyle 20+2x,~ 60-3x,~ (20+2x)(60-3x)\)
  3. (table)
  4. \(\displaystyle x= 20\)
  5. graph
  6. $24, $36
  7. $1350, $30, 45 rooms
4.2.5.21.
Answer.
  1. \(\displaystyle h=\dfrac{-1}{40}(x-80)^2+164\)
  2. 160.99 ft
4.2.5.23.
Answer.
5 g; 4 min
4.2.5.25.
Answer.
  1. graph
  2. \(\displaystyle (-4,0),~(0,2)\)
  3. \(~~~~\) \(x \lt -4\) \(-4 \lt x \lt 2\) \(x \gt 2\)
    \(Y_1\) \(-\) \(+\) \(+\)
    \(Y_2\) \(-\) \(-\) \(+\)
    \(Y_3\) \(+\) \(-\) \(+\)

4.3 Curve Fitting
4.3.5 Problem Set 4.3

Warm Up

4.3.5.1.
Answer.
\((4,10),~(0,-22),~(4 \pm \sqrt{5},0)\)
4.3.5.3.
Answer.
  1. \(\displaystyle 25-2x\)
  2. \(\displaystyle 30+4x\)
4.3.5.5.
Answer.
\(y=-x^2-2x+8\)
4.3.5.7.
Answer.
\(y=-x^2\)

Skills Practice

4.3.5.9.
Answer.
\((-2,3,-4)\)
4.3.5.11.
Answer.
\((1,-4,7)\)
4.3.5.13.
Answer.
\(a=3,~b=1,~c=-2\)

Applications

4.3.5.15.
Answer.
  1. \(\displaystyle y=a(x-5)^2-10=-0.2x^2+11x-78\)
  2. \(\displaystyle 42\)
4.3.5.17.
Answer.
\(D=\dfrac{1}{2}n^2 - \dfrac{3}{2}n\)
4.3.5.19.
Answer.
  1. \(\displaystyle N=-0.59t^2+7.33t-2.54\)
  2. \(\displaystyle 2000;~7\)
4.3.5.21.
Answer.
  1. \(\displaystyle (0,0.14)\)
  2. \(\displaystyle y=-1.786x^2+0.14\)

4.4 Quadratic Inequalities
4.4.6 Problem Set 4.4

Warm Up

4.4.6.1.
Answer.
  1. \(\displaystyle (-4,0),~(6,0)\)
  2. up
4.4.6.3.
Answer.
  1. \(\displaystyle (3 \pm \sqrt{12},0)\)
  2. down
4.4.6.5.
Answer.
  1. \(\displaystyle [0,4)\)
  2. \(\displaystyle (5,8)\)

Skills Practice

4.4.6.7.
Answer.
  1. grid
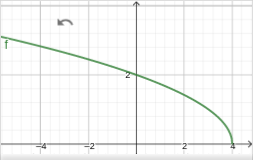
  2. See graph.
  3. \(x \gt 3\) or \(x \lt -1\)
4.4.6.9.
Answer.
  1. \(\displaystyle -12, 5\)
  2. \(x \lt -12\) or \(x \gt 15\)
4.4.6.11.
Answer.
  1. \(\displaystyle (-\infty,-3) \cup (6, \infty)\)
  2. \(\displaystyle (-3,6)\)
  3. \(\displaystyle [-2,5]\)
  4. \(\displaystyle (-\infty,2] \cup [5,\infty)\)
4.4.6.13.
Answer.
\(x \lt -2\) or \(x \gt 3\)
4.4.6.15.
Answer.
\(0 \le k \le 4\)
4.4.6.17.
Answer.
\((-6,-3)\)
4.4.6.19.
Answer.
\((-\infty, \dfrac{-1}{2}) \cup (4, \infty)\)
4.4.6.21.
Answer.
\((-\infty, -2.24) \cup (2.24, \infty)\)
4.4.6.23.
Answer.
All \(m\)
4.4.6.25.
Answer.
\(-4.8 \lt x \lt 6.2\)

Applications

4.4.6.27.
Answer.
\((-\infty, -4.2) \cup (2.6, \infty)\)
4.4.6.29.
Answer.
\(4 \t t \lt 16\) sec
4.4.6.31.
Answer.
\($5 \lt p \lt $7\)
4.4.6.33.
Answer.
  1. \(\displaystyle 60-x;~~12+\dfrac{1}{2}x\)
  2. \(\displaystyle y=(60-x)(12+\dfrac{1}{2}x)\)
  3. 882 bu; 18 trees
  4. Between 10 and 26, inclusive

4.5 Chapter 4 Summary and Review
4.5.3 Chapter 4 Review Problems

4.5.3.1.

Answer.
\(1,~2\)

4.5.3.2.

Answer.
\(\dfrac{3 \pm \sqrt{5}}{2}\)

4.5.3.3.

Answer.
\(-\dfrac{4 \pm \sqrt{8}}{2}\)

4.5.3.4.

Answer.
\(\dfrac{-2 \pm \sqrt{28}}{4}\)

4.5.3.5.

Answer.
\(\dfrac{6 \pm \sqrt{36-12h}}{6}\)

4.5.3.6.

Answer.
\(\dfrac{3 \pm \sqrt{9+8D}}{2}\)

4.5.3.7.

Answer.
one repeated real solution

4.5.3.8.

Answer.
two complex soutions

4.5.3.9.

Answer.
two complex soutions

4.5.3.10.

Answer.
two distinct real soutions

4.5.3.11.

Answer.
  1. \(\displaystyle h=100t-2.8t^2\)
  2. (graph)
  3. 893 ft
  4. \(15 \dfrac{5}{7}\) sec and 20 sec

4.5.3.12.

Answer.
  1. 1.5 sec, 11.025 m
  2. 7.056 m
  3. 0.6 sec
  4. 0.5 sec, 2.5 sec
  5. \((0,0),~(3,0).\) She leaves the springboard at \(t=0\) seconds and returns to the springboard at \(t=3\) seconds.

4.5.3.13.

Answer.
  1. \(\left(\dfrac{1}{2}, \dfrac{-49}{4}\right)\text{,}\) \((-3,0)\text{,}\) \((4,0)\text{,}\) \((0,-12)\)
  2. parabola

4.5.3.14.

Answer.
  1. \(\left(\dfrac{1}{4}, \dfrac{-31}{8}\right)\text{,}\) no \(x\)-intercepts,\(~(0,-4)\)
  2. parabola

4.5.3.15.

Answer.
  1. \(\displaystyle (1,5),~(-1.24,0),~(3.24,0),~(0,4)\)
  2. parabola

4.5.3.16.

Answer.
  1. \(\left(\dfrac{3}{2}, \dfrac{7}{4}\right),~\) no \(x\)-intercepts,\(~(0,4)\)
  2. parabola

4.5.3.17.

Answer.
\(y=0.2(x-15)^2-6\)

4.5.3.18.

Answer.
  1. \(\displaystyle (1,5)\)
  2. \(\displaystyle y=2x^2+4x+7\)

4.5.3.19.

Answer.
  1. 45
  2. $810

4.5.3.20.

Answer.
  1. \(\displaystyle R=1200x-80x^2\)
  2. $7.50
  3. $4500

4.5.3.21.

Answer.
  1. \(\displaystyle y=60(4+2x)(32-4x)\)
  2. 2

4.5.3.22.

Answer.
  1. \(\displaystyle R=(20+x)(500-10x)\)
  2. $35

4.5.3.23.

Answer.
\(a=1,~b=-1,~c=-6\)

4.5.3.24.

Answer.
\(y=-\dfrac{1}{2}x^2-4x+10\)

4.5.3.25.

Answer.
  1. \(\displaystyle h=36.98t+5.17\)
  2. 116.1 m, 153.1 m
  3. (graph)
  4. \(\displaystyle h=-4.858t^2+47.67t+0.89\)
  5. 100.2 m, 113.9 m
  6. (graph)
  7. quadratic

4.5.3.26.

Answer.
  1. \(\displaystyle y=-0.05x^2-0.003x+234.2\)
  2. \((-0.03, 234.2)~\) The velocity of the debris at its maximum height of 234.2 feet. The velocity there is actually zero.

4.5.3.27.

Answer.
\((-\infty,-2) \cup (3,\infty)\)

4.5.3.28.

Answer.
\([-3,4]\)

4.5.3.29.

Answer.
\([-1,\dfrac{3}{2}]\)

4.5.3.30.

Answer.
\((-\infty,-\dfrac{1}{3}) \cup (2,\infty)\)

4.5.3.31.

Answer.
\([-2,2]\)

4.5.3.32.

Answer.
\((-\infty,-\sqrt{3}) \cup (\sqrt{3},\infty)\)

4.5.3.33.

Answer.
  1. \(\displaystyle R=p(220-\dfrac{1}{4}p)\)
  2. \(\displaystyle 400 \lt p \lt 480\)

4.5.3.34.

Answer.
  1. \(\displaystyle R=p(30-\dfrac{1}{2}p)\)
  2. \(\displaystyle 20 \lt p \lt 40\)

5 Functions and Their Graphs
5.1 Functions
5.1.7 Problem Set 5.1

Warm Up

5.1.7.1.
Answer.
\(-24\)
5.1.7.3.
Answer.
\(\sqrt{20}\)
5.1.7.5.
Answer.
\(-3, \dfrac{1}{2}\)
5.1.7.7.
Answer.
\(\dfrac{14}{3}\)

Skills Practice

5.1.7.9.
Answer.
  1. input: \(v\text{,}\) output: \(x\)
  2. 15
  3. \(-1, \dfrac{5}{2}\text{.}\)
5.1.7.11.
Answer.
  1. \(\displaystyle \dfrac{-1}{3}\)
  2. \(\displaystyle \dfrac{-4}{9}\)
  3. \(\displaystyle \dfrac{-3}{4}\)
  4. \(\displaystyle -0.530\)

Applications

5.1.7.13.
Answer.
(b), (c), (e), and (f)
5.1.7.15.
Answer.
  1. 60
  2. 37.5
  3. 20
5.1.7.17.
Answer.
  1. \(\displaystyle h(1)=2\)
  2. 1 month
  3. 1 month
  4. 4000
5.1.7.19.
Answer.
  1. Approximately $1920
  2. $5 or $15
  3. \(\displaystyle f(12) \approx 1920;~~ f(5)=1500,~f(15)=1500\)
  4. \(\displaystyle 7\lt d\lt 13\)
5.1.7.21.
Answer.
  1. \(\displaystyle F(1992) = 7.5\%\)
  2. \(\displaystyle F(2000) = 4\%\)
  3. \(\displaystyle F(1998+ = 4.5\%,~ F(2001) = 4.5\%\)
5.1.7.25.
Answer.
  1. \(N(6000) = 2000\text{:}\) 2000 cars will be sold at a price of $6000.
  2. decrease
  3. 30,000. At a price of $30,000, they will sell 400 cars.

5.2 Graphs of Functions
5.2.6 Problem Set 5.2

Warm Up

5.2.6.1.
Answer.
y = 3x-4
5.2.6.3.
Answer.
y = 3x-4
5.2.6.5.
Answer.
  1. \(\displaystyle x \gt 0.6\)
    y = 1.4x - 0.64
  2. \(\displaystyle x \lt -0.4\)
    y = 1.4x - 0.64

Skills Practice

5.2.6.7.
Answer.
graph
5.2.6.9.
Answer.
graph

Applications

5.2.6.11.
Answer.
  1. \(\displaystyle -2, 0, 5\)
  2. 2
  3. \(\displaystyle h(-2)=0,~h(1)=0,~h(0)=-2\)
  4. 5
  5. 3
  6. increasing: \((-4,-2)\) and \((0,3)\text{;}\) decreasing: \((-2,0)\)
5.2.6.13.
Answer.
  1. \(\displaystyle 0, ~\dfrac{1}{2}, ~0\)
  2. \(\displaystyle \dfrac{5}{6}\)
  3. \(\displaystyle \dfrac{-5}{6},~\dfrac{-1}{6},~\dfrac{7}{6},~\dfrac{11}{6}\)
  4. \(\displaystyle 1,~-1\)
  5. Max at \(x=-1.5,~0.5\text{,}\) min at \(x=-0.5,~1.5\)
5.2.6.15.
Answer.
  1. \(f(1000) = 1495\text{:}\) The speed of sound at a depth of \(1000\) meters is approximately \(1495\) meters per second.
  2. \(d = 570\) or \(d = 1070\text{:}\) The speed of sound is \(1500\) meters per second at both a depth of \(570\) meters and a depth of \(1070\) meters.
  3. The slowest speed occurs at a depth of about \(810\) meters and the speed is about \(1487\) meters per second, so \(f(810) = 1487\text{.}\)
  4. \(f\) increases from about \(1533\) to \(1541\) in the first \(110\) meters of depth, then drops to about \(1487\) at \(810\) meters, then rises again, passing \(1553\) at a depth of about \(1600\) meters.
5.2.6.17.
Answer.
(a) and (d)
5.2.6.19.
Answer.
  1. \(\displaystyle -1, 1\)
  2. \(\displaystyle (-1,1)\)
  3. \(\displaystyle [-3,-2] \cup [2,3]\)
  4. \(\displaystyle [-5,5]\)
5.2.6.21.
Answer.
  1. \(\displaystyle -2,~2\)
  2. \(\displaystyle -2.8,~0,~2.8\)
  3. \(-2.5 \lt q \lt -1.25\) and \(1.25 \lt q \lt 2.5\)
  4. \(-2 \lt q \lt 0\) and \(2 \lt q\)
5.2.6.23.
Answer.
  1. \(\displaystyle g(-6)=0,~g(6)=0,~g(0)=6\)
  2. none
  3. \(g(x)\) is undefined for those \(x\)-values
5.2.6.25.
Answer.
  1. \(\displaystyle 0,~5\)
  2. \(\displaystyle 0,~\dfrac{-3}{2}\)
  3. \(\displaystyle \dfrac{5}{6}\)
  4. \(\displaystyle -5,~\dfrac{1}{2}\)
  5. parabola and line

5.3 Some Basic Graphs
5.3.4 Problem Set 5.3

Warm Up

5.3.4.1.
Answer.
  1. \(\displaystyle 4\)
  2. \(\displaystyle 2\)
5.3.4.3.
Answer.
  1. \(\displaystyle 2.080\)
  2. \(\displaystyle 6.366\)
  3. \(\displaystyle -0.126\)
  4. \(\displaystyle -1.458\)
5.3.4.5.
Answer.
  1. \(\displaystyle \dfrac{1}{2}\)
  2. \(\displaystyle \dfrac{-1}{3}\)
5.3.4.7.
Answer.
  1. \(\displaystyle -9\)
  2. \(\displaystyle 9\)
  3. \(\displaystyle 9\)
  4. \(\displaystyle -4\)
5.3.4.9.
Answer.
  1. \(\displaystyle -50 \)
  2. \(\displaystyle -43\)
  3. \(\displaystyle 144\)

Skills Practice

5.3.4.11.
Answer.
grid
5.3.4.13.
Answer.
square root of x
5.3.4.15.
Answer.
grid
5.3.4.17.
Answer.
  1. \(\displaystyle f\)
  2. \(\displaystyle g\)

Applications

5.3.4.19.
Answer.
\((-\infty,0) \cup [0.5,\infty) \)
5.3.4.21.
Answer.
(b): 2 units down, (c): 1 unit up
5.3.4.23.
Answer.
(b): 1.5 units left, (c): 1 unit right
5.3.4.25.
Answer.
(b): reflected about \(x\)-axis, (c): reflected about \(y\)-axis
5.3.4.27.
Answer.
  1. vi
  2. ii
  3. iv
  4. i
  5. v
  6. iii
5.3.4.29.
Answer.
  1. horizontal shift of square root \(y=\sqrt{x}\)
  2. vertical shift of cube root \(y=\sqrt[3]{x}\)
  3. vertical shift of absolute value \(y=\abs{x}\)
  4. vertical flip of reciprocal \(y=\dfrac{1}{x}\)
  5. vertical flip and vertical shift of cube \(y=x^3\)
  6. vertical flip and vertical shift of inverse-square \(y=\dfrac{1}{x^2} \)
5.3.4.31.
Answer.
  1. \(\displaystyle x \lt 2\)
  2. \(\displaystyle x \gt \dfrac{-2}{3}\)
5.3.4.33.
Answer.
  1. \(\displaystyle 41\)
  2. no solution
  3. \(\displaystyle 29\lt x\le 61\)

5.4 Direct Variation
5.4.6 Problem Set 5.4

Warm Up

5.4.6.1.
Answer.
  1. \(\displaystyle -10\)
  2. \(\displaystyle -16, 20\)

Skills Practice

5.4.6.3.
Answer.
  1. \(\displaystyle y=0.3x\)
  2. \(x\) \(2\) \(5\) \(8\) \(12\) \(15\)
    \(y\) \(-0.6\) \(1.5\) \(2.4\) \(3.6\) \(4.5\)
  3. \(y\) doubles also
5.4.6.5.
Answer.
(b), \(k=0.5\)
5.4.6.7.
Answer.
(c)

Applications

5.4.6.9.
Answer.
  1. \(\text{Price of item} \) \(18\) \(28\) \(12\)
    \(\text{Tax} \) \(1.17\) \(1.82\) \(0.78\)
    \(\text{Tax}/\text{Price} \) \(\alert{0.065}\) \(\alert{0.065}\) \(\alert{0.065}\)
    Yes; \(6.5\%\)
  2. \(\displaystyle T = 0.065p\)
  3. direct variation
5.4.6.11.
Answer.
  1. \(\displaystyle m = 0.165w\)
    \(w\) \(50\) \(100\) \(200\) \(400\)
    \(m\) \(\alert{8.25}\) \(\alert{16.5}\) \(\alert{33}\) \(\alert{66}\)
  2. 19.8 lb
  3. 303.03 lb
  4. It will double.
5.4.6.13.
Answer.
  1. \(\displaystyle v=15.306 d\)
  2. 3985 million light-years
  3. 18,979 km/sec
5.4.6.15.
Answer.
  1. \(\displaystyle P = \dfrac{1825}{8192}w^3\approx0.228w^3\)
    \(w\) \(10\) \(20\) \(40\) \(80\)
    \(P\) \(\alert{223} \) \(\alert{1782} \) \(\alert{14,259} \) \(\alert{114,074} \)
  2. 752 kilowatts
  3. 33.54 mph
  4. It is multiplied by 8.
5.4.6.17.
Answer.
  1. \(\displaystyle d = 0.005v^2\)
  2. 50 m
5.4.6.19.
Answer.
  1. \(\displaystyle W = 600d^2 \)
  2. 864 newtons
5.4.6.20.
Answer.
  1. Wind resistance quadruples.
  2. It is one-ninth as great.
  3. It is decreased by 19% because it is 81% of the original.

5.5 Inverse Variation
5.5.4 Problem Set 5.5

Warm Up

5.5.4.1.
Answer.
\(R=\dfrac{1}{3}I\text{.}\) Not inverse variation.
5.5.4.3.
Answer.
\(W=32,000-d\) Not inverse variation.

Skills Practice

5.5.4.5.
Answer.
(c)
5.5.4.7.
Answer.
  1. \(\displaystyle y=\dfrac{120}{x}\)
  2. \(x\) \(4\) \(8\) \(20\) \(30\) \(40\)
    \(y\) \(30\) \(15\) \(6\) \(4\) \(3\)
  3. \(y\) is divided by 2
5.5.4.9.
Answer.
(b), \(k=72\)
5.5.4.11.
Answer.
(c)

Applications

5.5.4.13.
Answer.
  1. \(\text{Width (feet)} \) \(2\) \(2.5\) \(3\)
    \(\text{Length (feet)} \) \(12\) \(9.6\) \(8\)
    \(\text{Length}\times \text{width} \) \(\alert{24}\) \(\alert{24}\) \(\alert{24}\)
    \(24\) square feet
  2. \(\displaystyle L = \dfrac{24}{w} \)
  3. inverse variation
5.5.4.15.
Answer.
  1. \(\displaystyle B = \dfrac{88}{d}\)
    \(d\) \(1\) \(2\) \(12\) \(24\)
    \(B\) \(\alert{88} \) \(\alert{44} \) \(\alert{7.3} \) \(\alert{3.7} \)
  2. \(8.8\) milligauss
  3. More than \(20.47\) in
  4. It is one half as strong.
5.5.4.17.
Answer.
  1. 645
  2. \(\displaystyle D=\dfrac{64,500}{n}\)
  3. 215
5.5.4.18.
Answer.
  1. \(\displaystyle m =\dfrac{8}{p} \)
  2. 0.8 ton
5.5.4.20.
Answer.
  1. \(\displaystyle T=\dfrac{4000}{d} \)
  2. \(8\degree\)C
5.5.4.22.
Answer.
  1. It is one-fourth the original illumination.
  2. It is one-ninth the illumination.
  3. It is 64% of the illumination.

5.6 Functions as Models
5.6.6 Problem Set 5.6

Warm Up

5.6.6.1.
Answer.
  1. \(\displaystyle (0, \infty)\)
  2. none
  3. \(\displaystyle (-infty, 0)\)
  4. none
5.6.6.3.
Answer.
  1. none
  2. \(\displaystyle (0, \infty)\)
  3. none
  4. none
5.6.6.5.
Answer.
  1. \(\displaystyle (-infty, 0)\)
  2. none
  3. \(\displaystyle (0, \infty)\)
  4. none
5.6.6.7.
Answer.
  1. \(\displaystyle s=h(t)\)
  2. After 3 seconds, the duck is at a height of 7 meters.

Skills Practice

5.6.6.9.
Answer.
  1. Increasing
  2. Concave up
5.6.6.11.
Answer.
\(y=\dfrac{k}{x}\)

Applications

5.6.6.13.
Answer.
(b)
5.6.6.15.
Answer.
(a)
5.6.6.17.
Answer.
(b)
5.6.6.19.
Answer.
  1. II
  2. IV
  3. I
  4. III
5.6.6.21.
Answer.
\(y = x^3\) stretched or compressed vertically
cubic
5.6.6.23.
Answer.
\(y =\dfrac{1}{x} \) stretched or compressed vertically
reciprocal
5.6.6.25.
Answer.
\(y =\sqrt{x} \)
root
5.6.6.27.
Answer.
  1. Table (4), Graph (C)
  2. Table (3), Graph (B)
  3. Table (1), Graph (D)
  4. Table (2), Graph (A)
5.6.6.29.
Answer.
  1. III
  2. 3

Absolute Value

5.6.6.1.
Answer.
  1. \(\displaystyle \abs{x}=6 \)
  2. number line
5.6.6.3.
Answer.
  1. \(\displaystyle \abs{p+3}=5 \)
  2. number line
5.6.6.5.
Answer.
  1. \(\displaystyle \abs{t-6}\lt 3 \)
  2. number line
5.6.6.7.
Answer.
  1. \(\displaystyle \abs{b+1}\ge 0.5 \)
  2. number line
5.6.6.9.
Answer.
absolute value graph
  1. \(x = -5\) or \(x = -1\)
  2. \(\displaystyle -7\le x\le 1\)
  3. \(x\lt -8\) or \(x\gt 2\)
5.6.6.11.
Answer.
absolute value graph
  1. \(\displaystyle x = 4\)
  2. No solution
  3. No solution
5.6.6.13.
Answer.
\(x=\dfrac{-3}{2} \) or \(x=\dfrac{5}{2} \)
5.6.6.15.
Answer.
\(q=\dfrac{-7}{3} \)
5.6.6.17.
Answer.
\(b=-14 \) or \(b=10 \)
5.6.6.19.
Answer.
\(w=\dfrac{13}{2} \) or \(w=\dfrac{15}{2} \)
5.6.6.21.
Answer.
No solution
5.6.6.23.
Answer.
No solution
5.6.6.25.
Answer.
\(\dfrac{-9}{2}\lt x \lt \dfrac{-3}{2} \)
5.6.6.27.
Answer.
\(d\le -2~ \) or \(~ d\ge 5 \)
5.6.6.29.
Answer.
All real numbers
5.6.6.31.
Answer.
\(1.4 \lt t\lt 1.6 \)
5.6.6.33.
Answer.
\(T\le 3.2~\) or \(~T\ge 3.3 \)
5.6.6.35.
Answer.
No solution

5.7 Chapter 5 Summary and Review
5.7.3 Chapter 5 Review Problems

5.7.3.1.

Answer.
A function: Each \(x\) has exactly one associated \(y\)-value.

5.7.3.2.

Answer.
Not a function

5.7.3.3.

Answer.
Not a function: The IQ of \(98\) has two possible SAT scores.

5.7.3.4.

Answer.
A function

5.7.3.5.

Answer.
\(N(10) = 7000\text{:}\) Ten days after the new well is opened, the company has pumped a total of \(7000\) barrels of oil.

5.7.3.6.

Answer.
\(H(16) = 3\text{:}\) At 16 mph, the trip takes 3 hours.

5.7.3.7.

Answer.
\(F(0) = 1, ~~F(-3) =\sqrt{37}\)

5.7.3.8.

Answer.
\(G(0) = -2, ~~G(20) =\sqrt[3]{12}\)

5.7.3.9.

Answer.
\(h(8) = -6, ~~h(-8) = -14\)

5.7.3.10.

Answer.
\(m(5) = 6, ~~m(-40) =-4.8\)

5.7.3.11.

Answer.
  1. \(\displaystyle P(0)=5\)
  2. x=5,~x=1

5.7.3.12.

Answer.
  1. R(0)=2
  2. \(\displaystyle x=2,~x=-2\)

5.7.3.13.

Answer.
  1. \(\displaystyle f (-2) = 3, ~~f (2) = 5\)
  2. \(\displaystyle t = 1, ~~t = 3\)
  3. \(t\)-intercepts \((-3, 0), (4, 0)\text{;}\) \(f (t)\)-intercept: \((0, 2)\)
  4. Maximum value of \(5\) occurs at \(t = 2\)

5.7.3.14.

Answer.
  1. \(\displaystyle P(-3)=-2, ~~P(3)=3\)
  2. \(\displaystyle z = -5,~ \dfrac{-1}{2},~4\)
  3. \((-4, 0), (-1, 0), (5,0)\text{;}\) \((0, 3)\)
  4. Maximum value of \(-3\) occurs at \(z = -2\)

5.7.3.15.

Answer.
Function

5.7.3.16.

Answer.
not a function

5.7.3.17.

Answer.
Not a function

5.7.3.18.

Answer.
Function

5.7.3.19.

Answer.
line

5.7.3.21.

Answer.
line

5.7.3.23.

Answer.
  1. \(\displaystyle x = \dfrac{1}{2}= 0.5\)
  2. \(\displaystyle x = \dfrac{27}{8}\approx 3.4\)
  3. \(\displaystyle x \gt 4.9\)
  4. \(\displaystyle x \le 2.0\)

5.7.3.24.

Answer.
  1. \(\displaystyle x = 0.4\)
  2. \(\displaystyle x = 3.2\)
  3. \(\displaystyle 0 \lt x \le 4.5\)
  4. \(x \lt 0\) or \(x \gt 0.2\)

5.7.3.25.

Answer.
  1. \(\displaystyle x\approx\pm 5.8 \)
  2. \(\displaystyle x = \pm 0.4\)
  3. \(-2.5\lt x \lt 0\) or \(0\lt x\lt 2.5\)
  4. \(x \le -0.5\) or \(x\ge 0.5\)

5.7.3.26.

Answer.
  1. \(\displaystyle x = 0.5\)
  2. \(\displaystyle x = 2.9\)
  3. \(\displaystyle 0 \le x \lt 2.3\)
  4. \(\displaystyle x \ge 1.7\)

5.7.3.27.

Answer.
\(y = 1.2x^2\)

5.7.3.28.

Answer.
\(y = 54x\)

5.7.3.29.

Answer.
\(y =\dfrac{20}{x} \)

5.7.3.30.

Answer.
\(y =\dfrac{720}{x^2} \)

5.7.3.31.

Answer.
  1. \(\displaystyle d = 1.75t^2\)
  2. 63 cm

5.7.3.32.

Answer.
  1. \(\displaystyle V=\dfrac{4T}{P}\)
  2. \(\displaystyle 32\)

5.7.3.33.

Answer.
\(480\) bottles

5.7.3.34.

Answer.
14.0625 lumens

5.7.3.35.

Answer.
  1. \(\displaystyle w = \dfrac{k}{r^2}\)
  2. inverse square in first quadrant
  3. \(3960\sqrt{3}\approx 6860\) miles

5.7.3.37.

Answer.
curve

5.7.3.38.

Answer.
oven temprature

5.7.3.39.

Answer.
inverse square

5.7.3.41.

Answer.
inverse square

5.7.3.43.

Answer.
  1. curve
  2. \(\displaystyle g(x)=\dfrac{24}{x} \)

5.7.3.44.

Answer.
  1. decreasing cubic
  2. \(\displaystyle F(x)=-x^3 \)

5.7.3.45.

Answer.
  1. \(x\) \(0\) \(4\) \(8\) \(14\) \(16\) \(22\)
    \(y\) \(24\) \(20\) \(16\) \(10\) \(8\) \(2\)
  2. \(\displaystyle y = 24 - x\)

5.7.3.46.

Answer.
  1. \(x\) \(0\) \(4\) \(10\) \(12\) \(14\) \(16\)
    \(y\) \(0\) \(6\) \(15\) \(18\) \(21\) \(24\)
  2. \(\displaystyle y = \dfrac{3}{2}x\)

5.7.3.47.

Answer.
  1. \(x\) \(0\) \(1\) \(4\) \(9\) \(16\) \(25\)
    \(y\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\)
  2. \(\displaystyle y = \sqrt{x} \)

5.7.3.48.

Answer.
  1. \(x\) \(0.25\) \(0.50\) \(1.00\) \(1.50\) \(2.00\) \(4.00\)
    \(y\) \(4.00\) \(2.00\) \(1.00\) \(0.67\) \(0.50\) \(0.25\)
  2. \(\displaystyle y = \dfrac{1}{x}\)

5.7.3.49.

Answer.
  1. \(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\)
    \(y\) \(5\) \(0\) \(-3\) \(-4\) \(-3\) \(0\)
  2. \(\displaystyle y = x^2-4 \)

5.7.3.50.

Answer.
  1. \(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(4\)
    \(y\) \(0\) \(5\) \(8\) \(9\) \(8\) \(-7\)
  2. \(\displaystyle y = 9 - x^2\)

6 Powers and Roots
6.1 Integer Exponents
6.1.5 Problem Set 6.1

Warm Up

6.1.5.1.
Answer.
  1. \(\displaystyle -2z^2\)
  2. \(\displaystyle -24z^4\)
6.1.5.3.
Answer.
  1. \(\displaystyle -12x^3y^4\)
  2. \(\displaystyle \dfrac{1}{4ab^4}\)
6.1.5.5.
Answer.
  1. \(\displaystyle 4x^{10}y^{14}\)
  2. \(\displaystyle x^4y\)

Skills Practice

6.1.5.7.
Answer.
  1. \(\displaystyle 9\)
  2. \(\displaystyle \dfrac{1}{9}\)
  3. \(\displaystyle 9\)
  4. \(\displaystyle \dfrac{1}{9}\)
  5. \(\displaystyle -9\)
  6. \(\displaystyle \dfrac{-1}{9}\)
6.1.5.9.
Answer.
  1. \(\displaystyle 40\)
  2. \(\displaystyle \dfrac{5}{8}\)
  3. \(\displaystyle \dfrac{5}{8}\)
  4. \(\displaystyle \dfrac{1}{40}\)
  5. \(\displaystyle 40\)
  6. \(\displaystyle \dfrac{8}{5}\)
6.1.5.11.
Answer.
  1. \(\displaystyle \dfrac{3}{4}\)
  2. \(\displaystyle \dfrac{1}{8}\)
  3. \(\displaystyle \dfrac{1}{2}\)
  4. \(\displaystyle \dfrac{9}{4}\)
  5. \(\displaystyle \dfrac{1}{6}\)
  6. \(\displaystyle 2\)
  7. \(\displaystyle \dfrac{4}{3}\)
  8. \(\displaystyle 8\)
6.1.5.13.
Answer.
  1. \(\displaystyle \dfrac{1}{(m-n)^2}\)
  2. \(\displaystyle \dfrac{1}{y^2}+\dfrac{1}{y^3}\)
  3. \(\displaystyle \dfrac{2p}{q^4}\)
  4. \(\displaystyle \dfrac{-5x^5}{y^2}\)
6.1.5.15.
Answer.
\(1.25\)
6.1.5.17.
Answer.
\(0.2\)
6.1.5.19.
Answer.
  1. \(\displaystyle \dfrac{20}{x^3}\)
  2. \(\displaystyle \dfrac{1}{3u^{12}}\)
  3. \(\displaystyle 5^8t\)
6.1.5.21.
Answer.
  1. \(\displaystyle \dfrac{1}{3}x+3x^{-1}\)
  2. \(\displaystyle \dfrac{1}{4}x^{-2}-\dfrac{3}{2}x^{-1}\)
6.1.5.23.
Answer.
\(x - 3 + 2x^{-1}\)
6.1.5.25.
Answer.
\(-4 - 2u^{-1} + 6u^{-2}\)
6.1.5.27.
Answer.
\(4x^{-2}(x^4 + 4)\)
6.1.5.29.
Answer.
  1. \(\displaystyle 2.85 \times 10^2\)
  2. \(\displaystyle 8.372 \times 10^6\)
  3. \(\displaystyle 2.4 \times 10^{-2}\)
  4. \(\displaystyle 5.23 \times 10^{-4}\)

Applications

6.1.5.31.
Answer.
  1. \(x\) \(1\) \(2\) \(4.5\) \(6.2\) \(9.3\)
    \(g(x)\) \(1\) \(0.125\) \(0.011\) \(0.0042\) \(0.0012 \)
  2. they decrease
  3. \(x\) \(1.5\) \(0.6\) \(0.1\) \(0.03\) \(0.002\)
    \(f(x)\) \(0.30\) \(4.63\) \(1000\) \(37,037\) \(125 \times 10^6\)
  4. they increase
6.1.5.33.
Answer.
  1. \(\displaystyle P = 0.355v^3\)
  2. \(v\approx 52.03\) mph
  3. 3.375
6.1.5.35.
Answer.
  1. \(\displaystyle d=50f^{-1}\)
  2. The are of the aperture decreases by a factor of 0.5 at each \(f\)-stop.
6.1.5.36.
Answer.
  1. \(\displaystyle 1.905 \times 10^{13}\)
  2. $57,552.87

6.2 Roots and Radicals
6.2.9 Problem Set 6.2

Skills Warm Up

6.2.9.1.
Answer.
\(13;~4;~3;~10;~6;~7\)
6.2.9.3.
Answer.
  1. \(\displaystyle 1.414\)
  2. \(\displaystyle 4.217\)
  3. \(\displaystyle 1.125\)
  4. \(\displaystyle 0.140\)
  5. \(\displaystyle 2.782\)
  6. \(\displaystyle 3.162\)

Skills Practice

6.2.9.5.
Answer.
  1. \(\displaystyle -3\)
  2. \(\displaystyle undefined\)
  3. \(\displaystyle -3\)
  4. \(\displaystyle -3\)
6.2.9.7.
Answer.
  1. \(\displaystyle \sqrt{7}\)
  2. \(\displaystyle 3\sqrt[4]{x} \)
  3. \(\displaystyle \sqrt[4]{3x}\)
6.2.9.9.
Answer.
  1. \(\displaystyle 5^{1/2}\)
  2. \(\displaystyle (4y)^{1/3}\)
  3. \(\displaystyle 5x^{1/3} \)
6.2.9.11.
Answer.
\(\dfrac{1}{4}x^{1/2}-2x^{-1/2}+\dfrac{1}{\sqrt{2}}x\)
6.2.9.13.
Answer.
\(x^{0.5}+x^{-0.25}-1\)
6.2.9.15.
Answer.
\(x = 91.125\)
6.2.9.17.
Answer.
\(x = \dfrac{19}{2} \)
6.2.9.19.
Answer.
\(x = \pm \sqrt{30} \)
6.2.9.21.
Answer.
\(L=\dfrac{gT^2}{4\pi^2} \)
6.2.9.23.
Answer.
\(M=\dfrac{d^3m}{16r^2}\)
6.2.9.25.
Answer.
\(A=\dfrac{E}{ST^4}\)
6.2.9.27.
Answer.
  1. I
  2. III
  3. II
  4. IV
6.2.9.29.
Answer.
  1. \(\displaystyle G(x) = 3.7x^{1/3} \)
  2. \(\displaystyle H(x) = 85^{1/4}x^{1/4} \)
  3. \(\displaystyle F(t) = 25t^{-1/5} \)

Applications

6.2.9.31.
Answer.
  1. \(L\) (feet) \(200\) \(400\) \(600\) \(800\) \(1000\)
    \(v_{\text{max}}\) (knots) \(18.4\) \(26\) \(31.8\) \(36.8\) \(41.1\)
  2. maximum velocity
  3. 50.4 knots
  4. maximum and cruise velocities
  5. 31 knots, 62%
6.2.9.33.
Answer.
  1. \(\displaystyle T=\dfrac{2\pi}{\sqrt{32}}L^{1/2} \)
  2. \(10.54\) sec
  3. square root
6.2.9.35.
Answer.
  1. $87.68; $72.00
  2. 1989; 2013
6.2.9.36.
Answer.
  1. \(6.5\times 10^{-13}\) cm; \(1.17\times 10^{-36} \text{ cm}^3\)
  2. \(\displaystyle 1.8\times 10^{14} g/\text{cm}^3\)
  3. Element Carbon Potassium Cobalt Technetium Radium
    Mass
    number, \(A\)     		\(14\) \(40\) \(60\) \(99\) \(226\)
    Radius, \(r\)
    (\(10^{-13}\) cm)    		 \(3.1\) \(4.4\) \(5.1\) \(6\) \(7.9\)
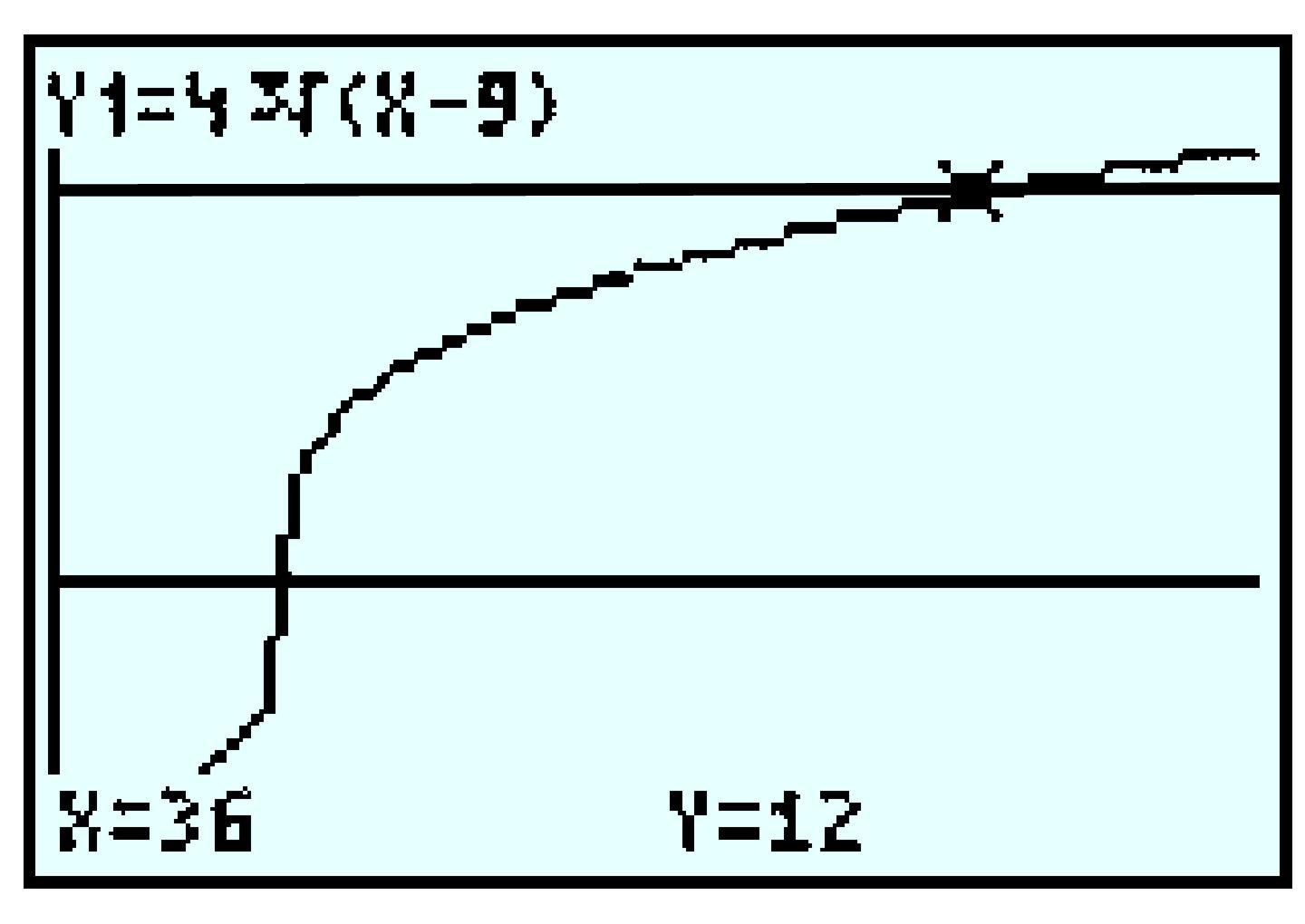
  4. cube root
6.2.9.37.
Answer.
132.6 km
6.2.9.39.
Answer.
  1. cube root
  2. \(\displaystyle x=36\)

6.3 Rational Exponents
6.3.6 Problem Set 6.3

Warm Up

6.3.6.1.
Answer.
  1. 4; 4
  2. 15.59; 15.59
  3. \(\displaystyle 8;~-81\)
6.3.6.3.
Answer.
  1. \(\displaystyle 2y^3\)
  2. \(\displaystyle 3x^2\)
  3. \(\displaystyle 2x^2y^9\)
  4. \(\displaystyle -3a^2b^3\)
  5. \(\displaystyle 4x^2y^6\)
  6. \(\displaystyle -2x^5y\)

Skills Practice

6.3.6.5.
Answer.
  1. \(\displaystyle \sqrt[4]{y^3}\)
  2. \(\displaystyle \dfrac{1}{\sqrt[7]{a^2}}\)
  3. \(\displaystyle \dfrac{1}{\sqrt[5]{s^3t^3}}\)
6.3.6.7.
Answer.
  1. \(\displaystyle y^{3/2}\)
  2. \(\displaystyle 6a^{3/5}b^{3/5}\)
  3. \(\displaystyle -2nq^{-11/8}\)
6.3.6.9.
Answer.
\(4a^2\)
6.3.6.11.
Answer.
\(4w^{3/2} \)
6.3.6.13.
Answer.
\(\dfrac{1}{2k^{1/4}} \)
6.3.6.15.
Answer.
\(x = 64\)
6.3.6.17.
Answer.
\(x = 1.157\)
6.3.6.19.
Answer.
\(29.524\)
6.3.6.21.
Answer.
\(\dfrac{13}{3} \)
6.3.6.23.
Answer.
\(2x-x^{2/3}\)
6.3.6.25.
Answer.
\(2x^{1/2} - x^{1/4} - 1 \)
6.3.6.27.
Answer.
\(x(x^{1/2} + 1)\)
6.3.6.29.
Answer.
\(\dfrac{a^{2/3}+a^{1/3}-1}{a^{1/3}} \)
6.3.6.31.
Answer.
\(x\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
\(f(x)\) \(0\) \(1\) \(2.5\) \(4.3\) \(6.4\) \(8.5\) \(10.9\)
\(g(x)\) \(0\) \(1\) \(2.8\) \(5.2\) \(8\) \(11.2\) \(14.7\)
power functions
6.3.6.33.
Answer.
  1. \(\displaystyle 2.83\)
  2. \(\displaystyle 3.30\)

Applications

6.3.6.35.
Answer.
  1. \(t\) \(5\) \(10\) \(15\) \(20\)
    \(I(t)\) \(131\) \(199\) \(254\) \(302\)
  2. 20 days
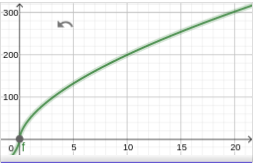
  3. graph
6.3.6.37.
Answer.
  1. \(A\) \(10\) \(100\) \(1000\) \(5000\) \(10,000\)
    \(S\) \(25 \) \(42 \) \(69 \) \(98 \) \(115 \)
  2. power function
  3. 81, 71
  4. 126,000 sq km
6.3.6.39.
Answer.
  1. 1.62
  2. 1.62
  3. 0.84; 0.84
6.3.6.41.
Answer.
  1. 15 days, 28 days
  2. \(\displaystyle \dfrac{I(m)\times W(m)}{m} = 0.18 m^{-0.041}\)
  3. \(m^{-0.041}\) is close to 1
6.3.6.43.
Answer.
  1. \(\displaystyle p=K^{1/2}a^{3/2}\)
  2. 1.88 years

6.4 Working with Radicals
6.4.6 Problem Set 6.4

Warm Up

6.4.6.1.
Answer.
No
6.4.6.3.
Answer.
Yes
6.4.6.5.
Answer.
\begin{equation*} ~\sqrt{ab} =\sqrt{a}\sqrt{b}~ \end{equation*}
\begin{equation*} ~\sqrt{\dfrac{a}{b}} =\dfrac{\sqrt{a}}{\sqrt{b}}~ \end{equation*}

Skills Practice

6.4.6.7.
Answer.
  1. \(\displaystyle 3\sqrt{2} \)
  2. \(\displaystyle 2\sqrt[3]{3} \)
  3. \(\displaystyle -2\sqrt[4]{4}=-2\sqrt{2} \)
6.4.6.9.
Answer.
  1. \(\displaystyle x^3 \sqrt[3]{x} \)
  2. \(\displaystyle 3z\sqrt{3z} \)
  3. \(\displaystyle 2a^2 \sqrt[4]{3a} \)
6.4.6.11.
Answer.
  1. \(\displaystyle 2\sqrt{4-x^2} \)
  2. \(\displaystyle A\sqrt[3]{8+A^3} \)
6.4.6.13.
Answer.
  1. \(\displaystyle \sqrt[3]{ab^2} \)
  2. \(\displaystyle x\sqrt{xy} \)
6.4.6.15.
Answer.
  1. \(\displaystyle 4\sqrt[3]{3} \)
  2. \(\displaystyle -\sqrt[3]{2} \)
6.4.6.17.
Answer.
  1. \(\displaystyle 6\sqrt{3}+6\sqrt{5}\)
  2. \(\displaystyle 3k\sqrt{3}-3k^2\sqrt{2}\)
6.4.6.19.
Answer.
  1. \(\displaystyle x-9\)
  2. \(\displaystyle -4+\sqrt{6}\)
6.4.6.21.
Answer.
  1. \(\displaystyle 3-\sqrt{5}\)
  2. \(\displaystyle \dfrac{-4+\sqrt{2}}{2}\)
  3. \(\displaystyle \dfrac{2a-\sqrt{2}}{2a}\)
6.4.6.23.
Answer.
  1. \(\displaystyle \dfrac{\sqrt{14x}}{6}\)
  2. \(\displaystyle \dfrac{\sqrt{2ab}}{b}\)
6.4.6.25.
Answer.
  1. \(\displaystyle -2{1-\sqrt{3}}\)
  2. \(\displaystyle \dfrac{x(x+\sqrt{3}}{x^2-3}\)

Applications

6.4.6.27.
Answer.
\(x^2+4x=(4-4\sqrt{5}+5)+(8+4\sqrt{5})=1\)
6.4.6.29.
Answer.
  1. \(\displaystyle \dfrac{w\sqrt{3}}{2}\)
  2. \(\displaystyle \dfrac{w^2\sqrt{3}}{4}\)

6.5 Radical Equations
6.5.6 Problem Set 6.5

Warm Up

6.5.6.1.
Answer.
  1. \(\displaystyle z=4\)
  2. \(\displaystyle w=8\)
6.5.6.3.
Answer.
  1. square root graph
  2. 13
6.5.6.5.
Answer.
  1. \(x\) \(y\)
    \(-25\) \(6.92\)
    \(-20\) \(6.71\)
    \(-15\) \(6.47\)
    \(-10\) \(6.15\)
    \(-5\) \(3.21\)
    \(0\) \(4\)
    \(5\) \(2.29\)
    \(10\) \(1.85\)
    \(15\) \(1.53\)
    \(20\) \(1.29\)
    grid
  2. \(\displaystyle -8\)

Skills Practice

6.5.6.7.
Answer.
\(\dfrac{-1}{3} \)
6.5.6.9.
Answer.
\(5 \)
6.5.6.11.
Answer.
\(5 \)
6.5.6.13.
Answer.
16
6.5.6.15.
Answer.
31
6.5.6.17.
Answer.
  1. \(\displaystyle 2\abs{x}\)
  2. \(\displaystyle \abs{x-5}\)
  3. \(\displaystyle \abs{x-3}\)

Applications

6.5.6.19.
Answer.
  1. 1.25 mi; 6600 ft
  2. \(\displaystyle h=(\dfrac{d}{89.4})^2\)
6.5.6.21.
Answer.
  1. 339.39 cubic in
  2. \(\displaystyle V=12.57r^3\)
6.5.6.23.
Answer.
\(b= \pm \sqrt{a^2-c^2}\)
6.5.6.25.
Answer.
\(W=\dfrac{v}{1-(\dfrac{D}{S})^3}\)

6.6 Chapter 6 Summary and Review
6.6.3 Chapter 6 Review Problems

6.6.3.1.

Answer.
  1. \(\displaystyle \dfrac{1}{81}\)
  2. \(\displaystyle \dfrac{1}{64}\)

6.6.3.2.

Answer.
  1. \(\displaystyle 9\)
  2. \(\displaystyle 75\)

6.6.3.3.

Answer.
  1. \(\displaystyle \dfrac{1}{243m^5}\)
  2. \(\displaystyle \dfrac{-7}{y^8}\)

6.6.3.4.

Answer.
  1. \(\displaystyle \dfrac{1}{a}+\dfrac{1}{a^2}\)
  2. \(\displaystyle \dfrac{3r^2}{q^9}\)

6.6.3.5.

Answer.
  1. \(\displaystyle \dfrac{2}{c^3}\)
  2. \(\displaystyle \dfrac{99}{z^2}\)

6.6.3.6.

Answer.
  1. \(\displaystyle \dfrac{d^8}{16k^{12}}\)
  2. \(\displaystyle \dfrac{2}{5}w^{14}\)

6.6.3.7.

Answer.
  1. \(1.018 \times 10{-9}~\)sec, or 0.000 000 001 018 sec
  2. 8 min 20 sec

6.6.3.8.

Answer.
1,200,000,000,000 hr, or 78,904,109,590 yr

6.6.3.9.

Answer.
  1. 5000 sec, or 83 min
  2. \(\displaystyle \dfrac{1}{10}\)
  3. 42 yr

6.6.3.10.

Answer.
  1. Planet Density
    Mercury 5426
    Venus 5244
    Earth 5497
    Mars 3909
    Jupiter 1241
    Saturn 620
    Uranus 1238
    Neptune 1615
    Pluto 2355
  2. Mercury, Venus, Earth, and Mars

6.6.3.11.

Answer.
  1. \(\displaystyle 25\sqrt{m} \)
  2. \(\displaystyle \dfrac{8}{\sqrt[3]{n}} \)

6.6.3.12.

Answer.
  1. \(\displaystyle \sqrt[3]{(13d)^3}\)
  2. \(\displaystyle 6\sqrt[5]{x^2y^3} \)

6.6.3.13.

Answer.
  1. \(\displaystyle \dfrac{1}{\sqrt[4]{27q^3}} \)
  2. \(\displaystyle 7\sqrt{u^3v^3} \)

6.6.3.14.

Answer.
  1. \(\displaystyle \sqrt{a^2+b^2} \)
  2. \(\displaystyle \sqrt[4]{16-x^2} \)

6.6.3.15.

Answer.
  1. \(\displaystyle 2x^{2/3} \)
  2. \(\displaystyle \dfrac{1}{4}x^{1/4} \)

6.6.3.16.

Answer.
  1. \(\displaystyle z^{5/2} \)
  2. \(\displaystyle z^{4/3} \)

6.6.3.17.

Answer.
  1. \(\displaystyle 6b^{-3/4} \)
  2. \(\displaystyle \dfrac{-1}{3}b^{-1/3} \)

6.6.3.18.

Answer.
  1. \(\displaystyle -4a^{-1/2} \)
  2. \(\displaystyle 2a^{-3/2} \)

6.6.3.19.

Answer.
112 kg

6.6.3.20.

Answer.
Height: 2.673 in; diameter: 5.346 in

6.6.3.21.

Answer.
  1. 480
  2. 498

6.6.3.22.

Answer.
  1. 294 sq in
  2. 90 lb

6.6.3.23.

Answer.
  1. increasing concave down
  2. 283
  3. 2051

6.6.3.25.

Answer.
  1. power function
  2. $7114.32

6.6.3.27.

Answer.
  1. It is the cost of producing the first ship.
  2. \(C = \dfrac{12}{ \sqrt[8]{x}} \) million
  3. About $11 million; about 8.3% ; about 8.3%>
  4. About 8.3%

6.6.3.29.

Answer.
  1. \(\displaystyle 4096\)
  2. \(\displaystyle \dfrac{1}{8}\)
  3. \(\displaystyle 36\sqrt{3} \approx 62.35\)
  4. \(\displaystyle 400,000\)

6.6.3.30.

Answer.
  1. \(\displaystyle -27\)
  2. \(\displaystyle \dfrac{-3}{4}\)
  3. \(\displaystyle -3\sqrt[3]{400} \approx -22.1\)
  4. \(\displaystyle -300\)

6.6.3.31.

Answer.
\(169\)

6.6.3.32.

Answer.
\(49\)

6.6.3.33.

Answer.
\(16\)

6.6.3.34.

Answer.
\(-16\)

6.6.3.35.

Answer.
\(1,~4\)

6.6.3.36.

Answer.
\(8\)

6.6.3.37.

Answer.
\(9\)

6.6.3.38.

Answer.
\(12\)

6.6.3.39.

Answer.
\(7\)

6.6.3.40.

Answer.
\(\pm 8\)

6.6.3.41.

Answer.
\(5\)

6.6.3.42.

Answer.
\(4\)

6.6.3.43.

Answer.
\(g=\dfrac{2v}{t^2} \)

6.6.3.44.

Answer.
\(r=\dfrac{\pm \sqrt{3q^2-6q+7}}{2} \)

6.6.3.45.

Answer.
\(p=\pm 2 \sqrt{R^2-R} \)

6.6.3.46.

Answer.
\(r=\pm \sqrt{2q^3-1} \)

6.6.3.47.

Answer.
  1. \(\displaystyle \dfrac{5p^4}{a^2}\sqrt{5p}\)
  2. \(\displaystyle \dfrac{2}{w^2}\sqrt[3]{3v^2}\)

6.6.3.48.

Answer.
  1. \(\displaystyle a^2b\)
  2. \(\displaystyle xy\)

6.6.3.49.

Answer.
  1. \(\displaystyle 2\sqrt[3]{a^3-2b^6}\)
  2. \(\displaystyle -4ab^2\sqrt[3]{2} \)

6.6.3.50.

Answer.
  1. \(\displaystyle 2t\sqrt{1+6t^4}\)
  2. \(\displaystyle 4t^4\sqrt{6} \)

6.6.3.51.

Answer.
  1. \(\displaystyle x^2-4x\sqrt{x}+4x\)
  2. \(\displaystyle x^2-4x\)

6.6.3.52.

Answer.
  1. \(\displaystyle 14-4\sqrt{6}\)
  2. \(\displaystyle 2a-4b\)

6.6.3.53.

Answer.
  1. \(\displaystyle \dfrac{7\sqrt{5y}}{5y}\)
  2. \(\displaystyle 3\sqrt{2d}\)

6.6.3.54.

Answer.
  1. \(\displaystyle \dfrac{\sqrt{33rs}}{11s}\)
  2. \(\displaystyle \dfrac{\sqrt{13m}}{m}\)

6.6.3.55.

Answer.
  1. \(\displaystyle \dfrac{-3\sqrt{a}+6}{a-4}\)
  2. \(\displaystyle \dfrac{-3\sqrt{z}-12}{z-16}\)

6.6.3.56.

Answer.
  1. \(\displaystyle \dfrac{2x^2+x\sqrt{3}-3}{x^2-3}\)
  2. \(\displaystyle \dfrac{5m^2-7m\sqrt{3}+6}{25m^2-12}\)

7 Exponential Functions
7.1 Exponential Growth and Decay
7.1.7 Problem Set 7.1

Warm Up

7.1.7.1.
Answer.
  1. $28
  2. #31.36
  3. No. It increase by 12% of different amounts.
7.1.7.3.
Answer.
Decreased by 1%.
7.1.7.5.
Answer.
4
7.1.7.7.
Answer.
\(\pm 1.2\)
7.1.7.9.
Answer.
\(-2.14\text{;}\) \(0.14\)

Skills Practice

7.1.7.11.
Answer.
  1. \(P = 1200 + 150t\text{;}\) 1650
  2. \(P = 1200\cdot 1.5^t\text{;}\) 4050
7.1.7.13.
Answer.
  1. \(V = 18,000 - 2000t\text{;}\) $8000
  2. \(V = 18,000\cdot 0.8^t\text{;}\) $5898.24
7.1.7.15.
Answer.
20%, 2%, 7.5%, 100%, 115%
7.1.7.17.
Answer.
  1. \(\displaystyle P_0 = 4,~ b = 2^{1/3}\)
  2. \(\displaystyle P(t) = 4\cdot 2^{t/3}\)
7.1.7.18.
Answer.
  1. Initial value \(80\text{,}\) decay factor \(\frac{1}{2}\)
  2. \(\displaystyle f(x) = 80\cdot \left(\dfrac{1}{2} \right)^x \)
7.1.7.19.
Answer.
The growth factor is \(1.2\text{.}\)
\(x\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(Q\) \(20\) \(24\) \(28.8\) \(34.56\) \(41.47\)
7.1.7.20.
Answer.
The decay factor is \(0.8\text{.}\)
\(w\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(N\) \(120\) \(96\) \(76.8\) \(61.44\) \(49.15\)
7.1.7.21.
Answer.
The decay factor is \(0.8\text{.}\)
\(t\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(C\) \(10\) \(8\) \(6.4\) \(5.12\) \(4.10\)
7.1.7.22.
Answer.
The growth factor is \(1.1\text{.}\)
\(n\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(B\) \(200\) \(220\) \(242\) \(266.2\) \(292.82\)

Applications

7.1.7.23.
Answer.
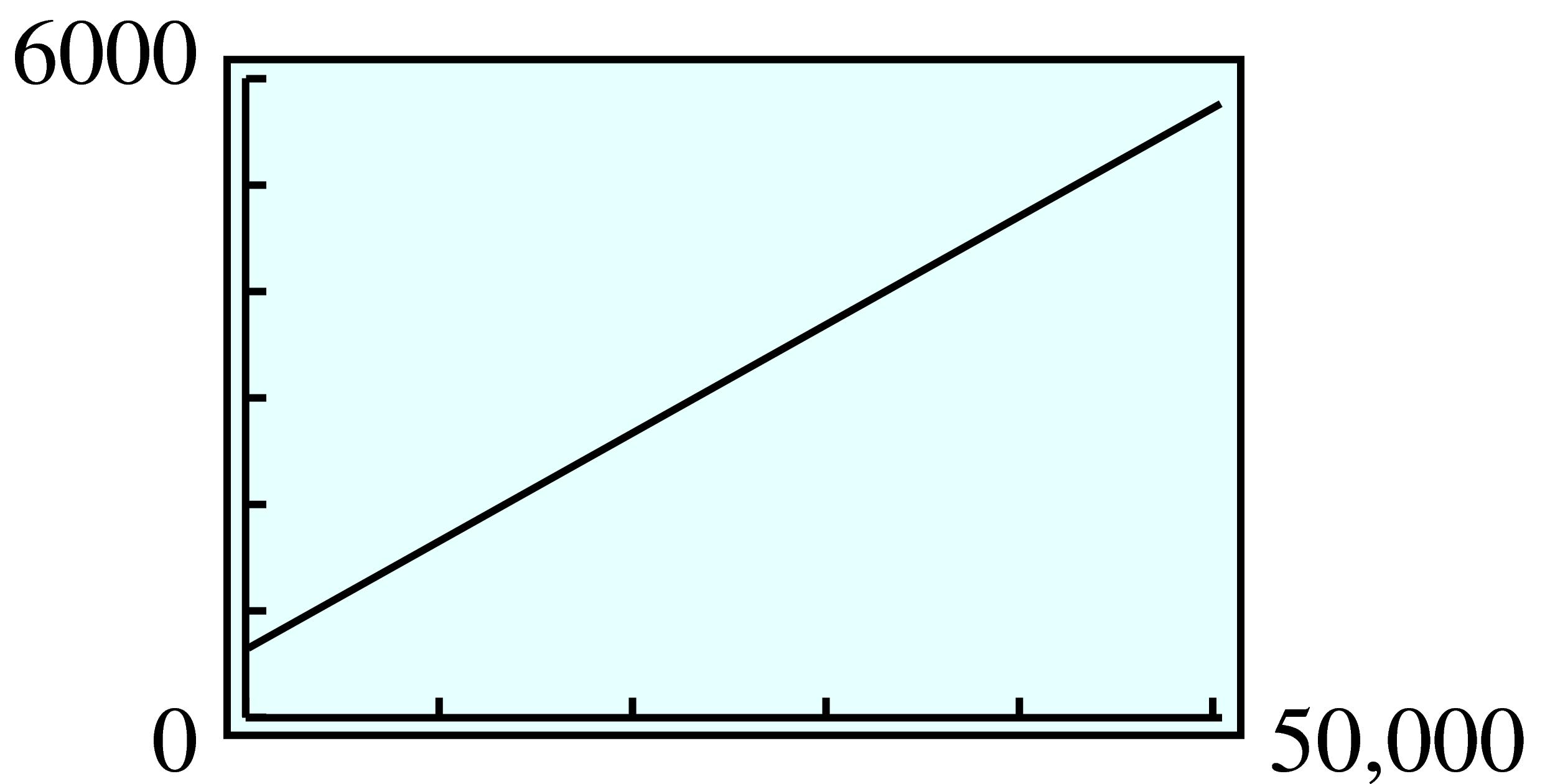
  1. Years after 2010 \(0\) \(1\) \(2\) \(3\) \(4\)
    Windsurfers \(1500\) \(1680\) \(1882\) \(2107\) \(2360\)
  2. \(\displaystyle S(t)=1200(1.12)^t\)
  3. Windsurfer sales exponential growth
  4. 2644; 5844
7.1.7.24.
Answer.
  1. Years after 1983 \(0\) \(5\) \(10\) \(15\) \(20\)
    Value of house \(20,000\) \(25,526\) \(32,578\) \(41,579\) \(53,066\)
  2. \(\displaystyle V(t)=200,000(1.05)^t\)
  3. house value
  4. $359,171.27; $458,403.66
7.1.7.25.
Answer.
  1. Weeks \(0\) \(6\) \(12\) \(18\) \(24\)
    Bees \(2000\) \(5000\) \(12,500\) \(31,250\) \(78,125\)
  2. \(\displaystyle P(t)=2000(2.5)^{t/6}\)
  3. bee population
7.1.7.27.
Answer.
  1. Weeks \(0\) \(2\) \(4\) \(6\) \(8\)
    Mosquitos \(250,000\) \(187,500\) \(140,625\) \(105,469\) \(79,102\)
  2. \(\displaystyle P(t)=250,000(0.75)^{t/2}\)
  3. graph
  4. 162,280; 68,504
7.1.7.29.
Answer.
  1. Years \(0\) \(3\) \(6\) \(9\) \(12\)
    Value of boat \(15,000\) \(13,500\) \(12,150\) \(10,935\) \(9841.50\)
  2. \(\displaystyle V(t)=15,000(0.885)^t\)
  3. motorboat depreciation
  4. $4995.52; $4421.04
7.1.7.31.
Answer.
  1. \(\displaystyle P(t)=1,545,387 b^t\)
  2. \(\displaystyle b=1.049;~ r=4.9\%\)
  3. 3,167,157
7.1.7.33.
Answer.
  1. 365
  2. exponential decay
  3. \(\displaystyle N(t)=365(0.356)^t\)
  4. 0.03
7.1.7.35.
Answer.
  1. 2440 tigers per decade
  2. 0.765; 23.5%
  3. 3080; 4656
7.1.7.37.
Answer.
  1. 39; 1.045
  2. 36; 1.047
  3. Species B

7.2 Exponential Functions
7.2.7 Problem Set 7.2

Warm Up

7.2.7.1.
Answer.
  1. \(\displaystyle 3^{x+4}\)
  2. \(\displaystyle 3^{4x}\)
  3. \(\displaystyle 12^x \)
7.2.7.3.
Answer.
  1. \(\displaystyle b^{-2t} \)
  2. \(\displaystyle b^{t/2} \)
  3. \(\displaystyle 1\)
7.2.7.5.
Answer.
\(0.06\)

Skills Practice

7.2.7.7.
Answer.
\(\dfrac{2}{3} \)
7.2.7.8.
Answer.
\(\dfrac{-1}{4} \)
7.2.7.9.
Answer.
\(\dfrac{1}{7} \)
7.2.7.11.
Answer.
\(\dfrac{-5}{4} \)
7.2.7.13.
Answer.
\(\pm 2 \)
7.2.7.15.
Answer.
\(2.26\)
7.2.7.17.
Answer.
  1. \((0,26)\text{;}\) increasing
  2. \((0,1.2)\text{;}\) decreasing
  3. \((0,75)\text{;}\) decreasing
  4. \((0,\frac{2}{3}) \text{;}\) increasing
7.2.7.18.
Answer.
  1. Power
  2. Exponential
  3. Power
  4. Neither
7.2.7.19.
Answer.
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\)
\(f(x)=3^x \) \(\frac{1}{27} \) \(\frac{1}{9} \) \(\frac{1}{3} \) \(1\) \(3\) \(9\) \(27\)
\(g(x)=\left(\frac{1}{3} \right)^x \) \(27\) \(9\) \(3\) \(1\) \(\frac{1}{3} \) \(\frac{1}{9} \) \(\frac{1}{27} \)
two exponentials
7.2.7.21.
Answer.
Because they are defined by equivalent expressions, (b), (c), and (d) have identical graphs.
7.2.7.23.
Answer.
\(0.17; 5.95\)
7.2.7.25.
Answer.
  1. \(\displaystyle P_0 = 800\)
  2. \(x\) \(0\) \(1\) \(2\)
    \(g(x)\) \(800\) \(200\) \(50\)
  3. \(\displaystyle a = \dfrac{1}{4}\)
  4. \(\displaystyle g(x) = 800(\dfrac{1}{4})^x\)
7.2.7.27.
Answer.
  1. Power \(y=100 x^{-1}\)
  2. Exponential \(P=\frac{1}{4} \cdot 2^x\)

Applications

7.2.7.28.
Answer.
  1. \(\displaystyle V(t) = 20,000(0.8)^{t/3}\)
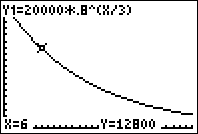
  2. GC decay
  3. 6 years
7.2.7.29.
Answer.
  1. \(\displaystyle N(t) = 26(2)^{t/6}\)
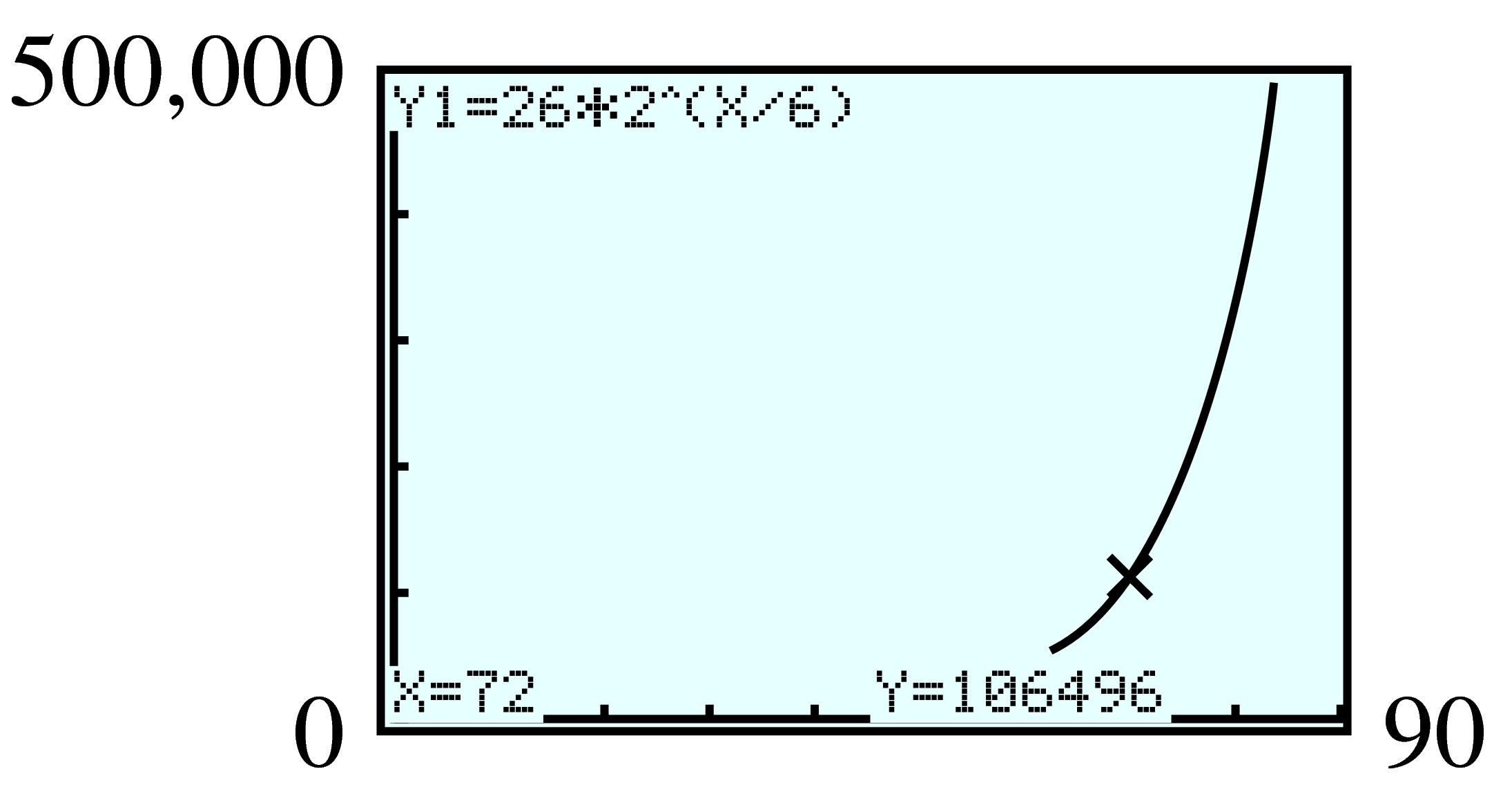
  2. GC growth
  3. 72 days later
7.2.7.30.
Answer.
  1. \(\displaystyle F_0=400\)
  2. \(\displaystyle b=1.06\)
  3. \(\displaystyle F(p) = 440(1.06)^p\)
7.2.7.31.
Answer.
  1. \(\displaystyle S_0=150\)
  2. \(\displaystyle b\approx 0.55\)
  3. \(\displaystyle S(d) = 150(0.55)^d\)
7.2.7.32.
Answer.
\(x\) \(f(x)=x^2\) \(g(x)=2^x \)
\(-2\) \(4\) \(\frac{1}{4} \)
\(-1\) \(1\) \(\frac{1}{2} \)
\(0\) \(0\) 1
\(1\) \(1\) \(2\)
\(2\) \(4\) \(4\)
\(3\) \(9\) \(8\)
\(4\) \(16\) \(16\)
\(5\) \(25\) \(32\)
exponential growth and qudratic
  1. \(\displaystyle Three\)
  2. \(\displaystyle x = -0.77,~2,~4\)
  3. \(\displaystyle (-0.77, 2) \cup (4,\infty)\)
  4. \(\displaystyle g(x)\)

7.3 Logarithms
7.3.7 Problem Set 7.3

Warm Up

7.3.7.1.
Answer.
  1. \(\displaystyle P(t)=300(1.15)^t\)
  2. \(\displaystyle 500=300(1.15)^t\)
  3. \(\displaystyle t \approx 3.65 \)

Skills Practice

7.3.7.3.
Answer.
  1. \(\displaystyle 2\)
  2. \(\displaystyle 4\)
7.3.7.5.
Answer.
  1. \(\displaystyle \dfrac{1}{2}\)
  2. \(\displaystyle -1\)
7.3.7.7.
Answer.
  1. \(\displaystyle -1\)
  2. \(\displaystyle 4\)
7.3.7.9.
Answer.
  1. \(\displaystyle 3 \lt x \lt 4\)
  2. \(\displaystyle -1 \lt y \lt 0\)
7.3.7.11.
Answer.
\(-0.23\)
7.3.7.13.
Answer.
\(0.77\)
7.3.7.15.
Answer.
\(2.53\)
7.3.7.17.
Answer.
  1. \(\displaystyle \log_t {16} = \dfrac{3}{2}\)
  2. \(\displaystyle \log_{0.8}{M} = 1.2\)
7.3.7.19.
Answer.
  1. \(\displaystyle 16^w = 256\)
  2. b^{-2} = 9
7.3.7.21.
Answer.
  1. \(\displaystyle x=\log_4{2.5} \approx 2.7\)
  2. \(\displaystyle x=\log_2{0.2} \approx -2.3\)
7.3.7.23.
Answer.
\(2.77\)

Applications

7.3.7.25.
Answer.
  1. 2030
  2. 6.2%
7.3.7.27.
Answer.
  1. 9.60 in
  2. 3.85 mi
7.3.7.29.
Answer.
  1. 2,018,436
  2. 5.17%
  3. 2008
7.3.7.31.
Answer.
  1. \(\displaystyle 4\)
  2. \(\displaystyle 4\)
  3. \(\displaystyle 64\)
  4. \(\displaystyle \sqrt[3]{16} \approx 2.52\)

7.4 Properties of Logarithms
7.4.5 Problem Set 7.4

Warm Up

7.4.5.1.
Answer.
  1. \(\displaystyle \log_8 {\dfrac{1}{2}} = \dfrac{-1}{3}\)
  2. \(\displaystyle \log_5 {46} = x\)
7.4.5.3.
Answer.
  1. \(\displaystyle 10^8\)
  2. \(2;~6;~8~\) Property (1)
7.4.5.5.
Answer.
  1. \(\displaystyle b^3\)
  2. \(8;~5;~3~\) Property (2)
7.4.5.7.
Answer.
  1. \(\displaystyle 10^{15}\)
  2. \(15;~3~\) Property (3)
7.4.5.9.
Answer.
  1. \(\displaystyle 5\)
  2. \(\displaystyle 6\)
  3. \(\displaystyle 5\)
(a) and (c) are equal.
7.4.5.11.
Answer.
  1. \(\displaystyle \log 24\approx 1.38\)
  2. \(\displaystyle \log 240\approx 2.38\)
  3. \(\displaystyle \log 230\approx 2.36\)
None are equal.

Skills Practice

7.4.5.13.
Answer.
  1. \(\displaystyle \log_t {16} = \dfrac{3}{2}\)
  2. \(\displaystyle \log_{0.8}{M} = 1.2\)
  3. \(\displaystyle \log_{3.7}{Q} = 2.5\)
  4. \(\displaystyle \log_3 {2N_0} = -0.2t\)
7.4.5.15.
Answer.
  1. \(\displaystyle x=\log_4{2.5} \approx 2.7\)
  2. \(\displaystyle x=\log_2{0.2} \approx -2.3\)
7.4.5.17.
Answer.
  1. \(\displaystyle \log_b 4\)
  2. \(\displaystyle \log_4(x^2y^3) \)
7.4.5.19.
Answer.
  1. \(\displaystyle \log 2x^{5/2} \)
  2. \(\displaystyle \log (t-4) \)
7.4.5.21.
Answer.
\(y = \dfrac{1}{25}\)
7.4.5.23.
Answer.
\(b = 100\)
7.4.5.25.
Answer.
\(2.81\)
7.4.5.27.
Answer.
\(-1.61\)
7.4.5.29.
Answer.
\(-12.49\)
7.4.5.31.
Answer.
  1. \(\displaystyle 1.7918\)
  2. \(\displaystyle -0.9163\)
7.4.5.34.
Answer.
(b) and (c)

Applications

7.4.5.37.
Answer.
  1. \(\displaystyle S (t) = S_0(1.09)^t\)
  2. \(4.7\) hours
7.4.5.39.
Answer.
  1. \(\displaystyle C(t) = 0.7(0.80)^t\)
  2. After 2.5 hours
  3. decay
7.4.5.41.
Answer.
  1. \(\displaystyle S(t) = S_0 \cdot 0.9527^t\)
  2. 28.61 hours
7.4.5.43.
Answer.
\(k=\dfrac{\log\left(\dfrac{N}{N_0}\right)}{t \log {a}} \)
7.4.5.45.
Answer.
\(t=\dfrac{1}{k}\log\left(\dfrac{A}{A_0}+1\right) \)

7.5 Exponential Models
7.5.4 Problem Set 7.5

Warm Up

7.5.4.1.
Answer.
4.16
7.5.4.3.
Answer.
16
7.5.4.5.
Answer.
\(y=\dfrac{-2}{3}x-1\)
7.5.4.7.
Answer.
\(y=\dfrac{-1}{2}x+4\)

Skills Practice

7.5.4.9.
Answer.
\(P(x)=8(0.5)^x\)
7.5.4.11.
Answer.
\(y=1.5(3){x/5}\)
7.5.4.13.
Answer.
  1. \(\displaystyle y=2.6-1.3x\)
  2. \(\displaystyle y=2.5(0,5)^x\)
  3. graph

Applications

7.5.4.15.
Answer.
\(P(t)=2000(2^{t/5};~\) 14.9%
7.5.4.17.
Answer.
\(D(t)=D_0(0,5^{t/18};~\) 3.8%
7.5.4.19.
Answer.
  1. \(\displaystyle P = P_0 (2)^{t/25 }\)
  2. 2.81%
7.5.4.21.
Answer.
  1. \(\dfrac{\log 0.5}{\log 0.946}\approx 12.5 \) hours
  2. 25 hours
  3. decay
7.5.4.23.
Answer.
  1. \(\displaystyle D(t)=D_0(0.5)^{t/15}\)
  2. After 89.5 years, or in 2060
7.5.4.25.
Answer.
  1. \(\displaystyle A = A_0 \left(\dfrac{1}{2} \right)^{t/5730}\)
  2. About 760 years old
7.5.4.27.
Answer.
12.9%
7.5.4.29.
Answer.
About 11 years

7.6 Chapter 7 Summary and Review
7.6.3 Chapter 7 Review Problems

7.6.3.1.

Answer.
  1. \(\displaystyle D = 8(1.5)^{t/5}\)
  2. \(18\text{;}\) \(44\)

7.6.3.3.

Answer.
  1. \(\displaystyle M = 100(0.85)^t\)
  2. \(52.2\) mg; \(19.7\) mg

7.6.3.5.

Answer.
growth

7.6.3.7.

Answer.
growth

7.6.3.9.

Answer.
\(\dfrac{-4}{3}\)

7.6.3.11.

Answer.
\(-11\)

7.6.3.13.

Answer.
\(4\)

7.6.3.15.

Answer.
\(-1\)

7.6.3.17.

Answer.
\(-3\)

7.6.3.19.

Answer.
\(2^{x-2} = 3\)

7.6.3.20.

Answer.
\(n^{p-1} = q\)

7.6.3.21.

Answer.
\(\log_{0.3}(x + 1) = -2\)

7.6.3.23.

Answer.
\(-1\)

7.6.3.25.

Answer.
\(4 \)

7.6.3.27.

Answer.
\(\dfrac{\log 5.1}{1.3}\approx 0.5433 \)

7.6.3.29.

Answer.
\(\dfrac{\log (2.9/3)}{-0.7}\approx 0.21 \)

7.6.3.31.

Answer.
0.054

7.6.3.32.

Answer.
2.959

7.6.3.33.

Answer.
0.195

7.6.3.34.

Answer.
2.823

7.6.3.35.

Answer.
\(\log_b x + \dfrac{1}{3} \log_b y - 2 \log_b z\)

7.6.3.37.

Answer.
\(\dfrac{4}{3} \log x -\dfrac{1}{3} \log y\)

7.6.3.39.

Answer.
\(\log\sqrt[3] {\dfrac{x}{y^{2}}} \)

7.6.3.41.

Answer.
\(\log {\dfrac{1}{8}} \)

7.6.3.43.

Answer.
\(\dfrac{\log 63}{\log 3}\approx 3.77 \)

7.6.3.45.

Answer.
\(\dfrac{\log 50}{-0.3\log 6}\approx -7.278 \)

7.6.3.47.

Answer.
\(\dfrac{\log(N/N_0)}{k}\)

7.6.3.49.

Answer.
  1. \(\displaystyle 238\)
  2. \(\displaystyle 2010\)

7.6.3.51.

Answer.
  1. \(\displaystyle C = 90(1.06)^t\)
  2. $\(94.48\)
  3. \(5\) years

8 Polynomial and Rational Functions
8.1 Polynomial Functions
8.1.6 Problem Set 8.1

Warm Up

8.1.6.1.
Answer.
  1. \(\displaystyle a^2 + 2ab + b^2\)
  2. \(\displaystyle a^2 - 2ab + b^2\)
8.1.6.3.
Answer.
  1. \(\displaystyle (x-7)^2\)
  2. cannot be factored
  3. \(\displaystyle (x+3)^2\)
  4. \(\displaystyle (x+8)(x-8)\)

Skills Practice

8.1.6.5.
Answer.
(b) and (c) are not polynomials; they have variables in a denominator.
8.1.6.7.
Answer.
  1. \(\displaystyle -1.9x^3+x+6.4\)
  2. \(\displaystyle -2x^2+6xy+2y^3\)
8.1.6.9.
Answer.
  1. 4
  2. 5
  3. 7
8.1.6.11.
Answer.
  1. \(\displaystyle 6a^4-5a^3-5a^2+5a-1\)
  2. \(\displaystyle y^4+5y^3-20y-16\)
8.1.6.13.
Answer.
  1. \(\displaystyle 1+15\sqrt{t}+75t+125t\sqrt{t}\)
  2. \(\displaystyle 1-\dfrac{9}{a}+\dfrac{27}{a^2}-\dfrac{27}{a^3}\)
8.1.6.15.
Answer.
  1. \(\displaystyle 27a^3-8b^3\)
  2. \(\displaystyle 8a^3 + 27b^3\)
8.1.6.17.
Answer.
\((a-2b)(a^2+2ab+4b^2)\)
8.1.6.19.
Answer.
\((3a+4b)(9a^2-12ab+16b^2)\)
8.1.6.21.
Answer.
\((4t^3+w^2)(16t^6-4t^3w^2+w^4)\)

Applications

8.1.6.23.
Answer.
  1. length: \(w+3\text{;}\) height: \(w-2\)
  2. \(\displaystyle w^3+w^2-6w\)
  3. \(\displaystyle 5w^2+w-12\)
8.1.6.25.
Answer.
  1. \(\displaystyle \dfrac{2}{3}\pi r^3+\pi r^2h \)
  2. \(\displaystyle V(r)=\dfrac{14}{3}\pi r^3 \)
8.1.6.27.
Answer.
  1. \(\displaystyle 0, 9\)
  2. \(0\le x \le 9\text{;}\) \(R\ge 0\) for these values
  3. cubic
  4. \(\dfrac{28}{3} \) points
  5. \(36\) points
  6. \(3\) ml or \(8.2\) ml
8.1.6.29.
Answer.
  1. \(20\) cm
  2. \(100\) cm
8.1.6.31.
Answer.
  1. \(\displaystyle 6 + x + 5x^2\)
  2. \(\displaystyle 4 - 7x^2 - 8x^4\)

8.2 Algebraic Fractions
8.2.5 Problem Set 8.2

Warm Up

8.2.5.1.
Answer.
  1. \(\dfrac{-3}{5} \text{,}\) \(\dfrac{3}{7} \)
  2. \(\displaystyle 3 \)
  3. \(\displaystyle -1\)
8.2.5.3.
Answer.
  1. \(\dfrac{-4}{3} \text{,}\) \(\dfrac{40}{399} \)
  2. \(\displaystyle 1,~-1 \)
  3. \(\displaystyle 0\)
8.2.5.5.
Answer.
  1. \(\displaystyle \dfrac{5}{x}\)
  2. \(\displaystyle \dfrac{12b}{7} \)
8.2.5.7.
Answer.
  1. \(\displaystyle \dfrac{-8}{5} \)
  2. \(\displaystyle \dfrac{a}{9}\)

Skills Practice

8.2.5.9.
Answer.
None are correct
8.2.5.11.
Answer.
  1. cannot be reduced
  2. \(\displaystyle 1\)
  3. cannot be reduced
  4. cannot be reduced
8.2.5.13.
Answer.
(b)
8.2.5.15.
Answer.
(a)
8.2.5.17.
Answer.
\(\dfrac{a}{a-3}\)
8.2.5.19.
Answer.
\(\dfrac{1}{a+b}\)
8.2.5.21.
Answer.
\(\dfrac{y+3x}{y-3x}\)
8.2.5.23.
Answer.
\(y-2\)
8.2.5.25.
Answer.
\(\dfrac{-a}{a+1}\)
8.2.5.27.
Answer.
\(\dfrac{4z^2+6z+9}{2z+3}\)

Applications

8.2.5.29.
Answer.
  1. 30 min
  2. 50 min
  3. 50 min
  4. 6 mph
  5. The time increases. If the current is 10 mph, the team will not be able to row upstream
8.2.5.31.
Answer.
  1. \(\displaystyle 0\le p \lt 100\)
  2. \(p\) \(0\) \(25\) \(50\) \(75\) \(90\) \(100\)
    \(C\) \(0\) \(120\) \(360\) \(1080\) \(3240\) \(-- \)
  3. curve
    60%
  4. \(\displaystyle p\lt 80\%\)
  5. \(p=100\text{:}\) The cost of extracting more ore grows without bound as the amount extracted approaches 100%.
8.2.5.33.
Answer.
  1. \(\dfrac{200}{2x-1} \) square centimeters
  2. 8; If \(x=13\text{,}\) the area of the cross-section is 8 \(\text{cm}^2\text{.}\)
8.2.5.35.
Answer.
  1. \(4500+\dfrac{3000}{x} \text{;}\) \(C(x) = 6x + 4500 + \dfrac{3000}{x} \)
  2. \(x\) \(20\) \(40\) \(60\) \(80\) \(100\)
    \(C\) \(4770 \) \(4815 \) \(5018 \) \(5130 \)
  3. $4768.33
    rational function
  4. 22; 14>
  5. rational function with slant asymptote
    The graph of \(C\) approaches the line as an asymptote.

8.3 Operations on Algebraic Fractions
8.3.8 Problem Set 8.3

Warm Up

8.3.8.1.
Answer.
  1. \(\displaystyle \dfrac{4}{15} \)
  2. \(\displaystyle \dfrac{2z}{3w}\)
8.3.8.3.
Answer.
  1. \(\displaystyle 28\)
  2. \(\displaystyle 28\)
8.3.8.5.
Answer.
  1. \(\displaystyle \dfrac{1}{6}\)
  2. \(\displaystyle \dfrac{1}{6y^2}\)

Skills Practice

8.3.8.7.
Answer.
  1. \(\displaystyle \dfrac{-36a^2}{7} \)
  2. \(\displaystyle \dfrac{8b}{3b+3}\)
  3. \(\displaystyle \dfrac{v^2}{1-v^2}\)
8.3.8.9.
Answer.
\(\dfrac{1}{8x}\)
8.3.8.11.
Answer.
\(\dfrac{a(2a-1)}{a+4}\)
8.3.8.13.
Answer.
\(\dfrac{6x(x-2)(x-1)^2}{(x^2-8)(x^2-2x+4)}\)
8.3.8.15.
Answer.
\(\dfrac{9a^3}{14b^3}\)
8.3.8.17.
Answer.
\(\dfrac{3a}{2}\)
8.3.8.19.
Answer.
\(\dfrac{x^2}{y-1}\)
8.3.8.21.
Answer.
\(\dfrac{(z+2)^2}{z^2(2z-1)}\)
8.3.8.23.
Answer.
\((x-y)(4x^2+2xy+y^2)\)
8.3.8.25.
Answer.
\(\dfrac{2x+y}{3x}\)
8.3.8.27.
Answer.
\(z-3\)
8.3.8.29.
Answer.
\(\dfrac{10x+3}{4x^2}\)
8.3.8.31.
Answer.
\(\dfrac{13}{8a-4b}\)
8.3.8.33.
Answer.
\(\dfrac{h^2+2h-3}{h+2}\)
8.3.8.35.
Answer.
\(\dfrac{6x-x^2-4}{x(x-2)}\)
8.3.8.37.
Answer.
\(\dfrac{19}{6(p-2)}\)
8.3.8.39.
Answer.
\(\dfrac{5k+1}{k(k-3)(k+1)}\)
8.3.8.41.
Answer.
\(\dfrac{3y-3y^2}{(y+1)(2y-1)}\)
8.3.8.43.
Answer.
\(12xy^2(x+y)^2\)
8.3.8.45.
Answer.
\(x(x-1)^3\)

Applications

8.3.8.47.
Answer.
\(\dfrac{4LR}{D^2}\)
8.3.8.49.
Answer.
\(\dfrac{2L}{c}+\dfrac{2LV^2}{c^3}\)
8.3.8.51.
Answer.
\(\dfrac{3q}{8\pi R}-\dfrac{a^2q}{8 \pi R^3}\)
8.3.8.53.
Answer.
\(-8t +\dfrac{1}{4} - \dfrac{3}{t}\)
8.3.8.55.
Answer.
  1. \(\displaystyle \dfrac{x}{2}\)
  2. \(\displaystyle 2x\)
  3. \(\displaystyle \dfrac{1}{2x}\)
8.3.8.57.
Answer.
  1. \(\displaystyle \dfrac{1}{a+b}\)
  2. \(\displaystyle \dfrac{3}{4(a+b)}\)
  3. \(\displaystyle \dfrac{4}{3(a+b)}\)
8.3.8.59.
Answer.
\(\dfrac{-H+ST}{RT}\)
8.3.8.61.
Answer.
\(\dfrac{4L-R^2C}{4L^2C}\)
8.3.8.63.
Answer.
\(\dfrac{2r^2_2ra+a^2}{a^2}\)
8.3.8.65.
Answer.
  1. \(\dfrac{144}{x^2-2x}\) sq ft
  2. \(\displaystyle \dfrac{48x-48}{x^2-2x} ft\)
8.3.8.67.
Answer.
  1. \(\dfrac{900}{400+w}\) hr
  2. \(\dfrac{900}{400-w}\) hr
  3. Orville, by \(\dfrac{1800w}{160,000-w^2}\) hr

8.4 More Operations on Fractions
8.4.5 Problem Set 8.4

Warm Up

8.4.5.1.
Answer.
\(\dfrac{2x^2+x-2}{x(x-1)} \)
8.4.5.3.
Answer.
\(\dfrac{x+2}{x-1} \)

Skills Practice

8.4.5.5.
Answer.
\(6y\)
8.4.5.7.
Answer.
\(\dfrac{5}{16}\)
8.4.5.9.
Answer.
\(\dfrac{7}{10a+2}\)
8.4.5.11.
Answer.
\(\dfrac{2x+1}{x}\)
8.4.5.13.
Answer.
\(\dfrac{nq}{p+q}\)
8.4.5.15.
Answer.
\(\dfrac{u-v}{xv}\)
8.4.5.17.
Answer.
\(\dfrac{1}{2}x^2\dfrac{1}{2}-\dfrac{1}{3x^2}\)
8.4.5.19.
Answer.
\(x-2+\dfrac{3}{y}\)
8.4.5.21.
Answer.
\(2y+5+\dfrac{2}{2y+1)}\)
8.4.5.23.
Answer.
\(4z^3-2z^2+3z+1+\dfrac{2}{2z+1}\)

Applications

8.4.5.25.
Answer.
\(\overline{PQ}\) and \(overline{RS}: ~\dfrac{b}{a}\text{;}\) \(\overline{QR}\) and \(overline{SP}: ~\dfrac{b}{a}\)
8.4.5.27.
Answer.
  1. \(\displaystyle \dfrac{1}{f}=\dfrac{2q+60}{q^2+60q} \)
  2. \(\displaystyle f=\dfrac{q^2+60q}{2q+60} \)
8.4.5.29.
Answer.
\(\dfrac{n^2-k^2}{n^2}\)
8.4.5.31.
Answer.
\(\dfrac{2cd}{c^2-u^2}\)
8.4.5.33.
Answer.
\(\dfrac{KL}{N(L-F)}\)
8.4.5.35.
Answer.
\(\dfrac{1}{m+2h}\)
8.4.5.37.
Answer.
\(\dfrac{x^2+y^2}{x^2y^2}\)
8.4.5.39.
Answer.
\(\dfrac{b^2-a^2}{ab}\)
8.4.5.41.
Answer.
\(\dfrac{y}{y-x}\)
8.4.5.43.
Answer.
\(\dfrac{\sqrt{15}}{3}\)
8.4.5.45.
Answer.
\(\dfrac{2\sqrt{3}+\sqrt{6}}{9}\)
8.4.5.47.
Answer.
\(\dfrac{6\sqrt{3}+7\sqrt{2}}{5}\)

8.5 Equations with Fractions
8.5.7 Problem Set 8.5

Warm Up

8.5.7.1.
Answer.
\(\dfrac{-1}{2} \)
8.5.7.3.
Answer.
\(\dfrac{13}{8} \)
8.5.7.5.
Answer.
\(\pm\sqrt{\dfrac{15}{8}} \)
8.5.7.7.
Answer.
\(\dfrac{1800}{1849}\approx 0.97 \)

Skills Practice

8.5.7.9.
Answer.
\(-2,~1\)
8.5.7.11.
Answer.
\(-6\)
8.5.7.13.
Answer.
\(1\)
8.5.7.15.
Answer.
\(\dfrac{-14}{5}\)
8.5.7.17.
Answer.
We don’t multiply by the LCD in addition problems.
8.5.7.19.
Answer.
\(r=\dfrac{S-a}{a}\)
8.5.7.21.
Answer.
\(x=a-\dfrac{ay}{b}\)
8.5.7.23.
Answer.
\(R=\dfrac{Cr}{r-C}\)

Applications

8.5.7.25.
Answer.
2 mph
8.5.7.27.
Answer.
24 days
8.5.7.29.
Answer.
\(168=\dfrac{72p}{100-p}\text{;}\) \(p=70\%\)
8.5.7.31.
Answer.
  1. 0.268
  2. \(\displaystyle \dfrac{44+x}{164+x}\)
  3. 21
8.5.7.33.
Answer.
  1. \(\displaystyle t=\dfrac{144}{v-20}\)
  2. \(\displaystyle t=\dfrac{144}{v+20}\)
  3. \(\displaystyle (100,3)\)
  4. \(\displaystyle t=\dfrac{144}{v-20} + t=\dfrac{144}{v+20} = 3\)
  5. 100 mph
8.5.7.35.
Answer.
\(28 \dfrac{1}{3}\) miles
8.5.7.37.
Answer.
  1. \(\displaystyle AE = 1,~ DE = x - 1,~ CD = 1\)
  2. \(\displaystyle \dfrac{1}{x}=\dfrac{x-1}{x} \)
  3. \(\displaystyle \dfrac{1+\sqrt{5}}{2} \)
8.5.7.39.
Answer.
Because \(x=1\text{,}\) dividing by \(x-1\) in the fourth step is dividing by \(0\text{.}\)
8.5.7.41.
Answer.
  1. two rational functions
  2. \(\displaystyle x=\dfrac{1}{2} \)

8.6 Chapter 8 Summary and Review
8.6.3 Chapter 8 Review Problems

8.6.3.1.

Answer.
\(2x^3-11x^2+19x-10\)

8.6.3.3.

Answer.
\((2x-3z)(4x^2+6xz+9z^2)\)

8.6.3.5.

Answer.
  1. \(\displaystyle \dfrac{1}{6}n^3-\dfrac{1}{2}n^2+\dfrac{1}{3}n \)
  2. \(\displaystyle 220\)
  3. \(\displaystyle 20\)

8.6.3.7.

Answer.
  1. \(\displaystyle V=\dfrac{\pi h^3}{4} \)
  2. \(2\pi\text{ cm}^3 \approx 6.28\text{ cm}^3 \text{;}\) \(16\pi\text{ cm}^3 \approx 50.27\text{ cm}^3 \)
  3. cubic

8.6.3.9.

Answer.
  1. rational function
  2. 338
  3. Months 2 and 02
  4. During month 6. The number of members eventually decreases to zero.

8.6.3.11.

Answer.
  1. \(\displaystyle t_1=\dfrac{90}{v-2} \)
  2. \(\displaystyle t_2=\dfrac{90}{v+2} \)
  3. curve
  4. \(\displaystyle \dfrac{90}{v-2}+\dfrac{90}{v+2}=24 \)
  5. 8 mph

8.6.3.13.

Answer.
\(\dfrac{a}{2(a-1)}\)

8.6.3.15.

Answer.
\(\dfrac{y^2-2x}{2}\)

8.6.3.17.

Answer.
\(\dfrac{a-3}{2a+6)}\)

8.6.3.19.

Answer.
\(10ab\)

8.6.3.21.

Answer.
\(\dfrac{6x}{2x+3}\)

8.6.3.23.

Answer.
\(\dfrac{a^2-2a}{a^2+3a+2}\)

8.6.3.25.

Answer.
\(\dfrac{1}{2x-1}\)

8.6.3.27.

Answer.
\(9x^2-7+\dfrac{4}{x^2}-\dfrac{1}{x^4} \)

8.6.3.29.

Answer.
\(x^2-2x-2-\dfrac{1}{x-2}\)

8.6.3.31.

Answer.
\(\dfrac{2}{x}\)

8.6.3.33.

Answer.
\(\dfrac{3x+1}{2(x-3)(x+3)}\)

8.6.3.35.

Answer.
\(\dfrac{2a^2-a+1}{(a-3)(a-1{})}\)

8.6.3.37.

Answer.
\(\dfrac{1}{5}\)

8.6.3.39.

Answer.
\(\dfrac{x}{x+4} \)

8.6.3.41.

Answer.
\(-2\)

8.6.3.43.

Answer.
No solution

8.6.3.45.

Answer.
\(n=\dfrac{Ct}{C-V} \)

8.6.3.47.

Answer.
\(q=\dfrac{pr}{r-p} \)

8.6.3.49.

Answer.
\(\dfrac{x^3+y}{x^3y}\)

8.6.3.51.

Answer.
\(\dfrac{1-x^2y^2}{xy}\)

8.6.3.53.

Answer.
\(\dfrac{-(x-y)^2}{xy}\)

9 Equations and Graphs
9.1 Properties of Lines
9.1.4 Problem Set 9.1

Warm Up

9.1.4.1.
Answer.
  1. \(A:\)negative; \(B:\) negative; \(C:\) positive; \(D:\) zero
  2. \(B\text{,}\) \(A\text{,}\) \(D\text{,}\) \(C\)
9.1.4.3.
Answer.
Number Negative
reciprocal		 Their
product
\(\dfrac{2}{3} \) \(\dfrac{-3}{2} \) \(-1 \)
\(\dfrac{-5}{2} \) \(\dfrac{2}{5}\) \(-1\)
\(6 \) \(\dfrac{-1}{6} \) \(-1\)
\(-4\) \(\dfrac{1}{4} \) \(-1\)
\(-1 \) \(1\) \(-1\)

Skills Practice

9.1.4.5.
Answer.
  1. verticl line
  2. \(m\) is undefined; \((4,0)\)
9.1.4.7.
Answer.
\(x=-5\)
9.1.4.9.
Answer.
\(y=6\)
9.1.4.11.
Answer.
parallel: a, g, h; perpendicular: c, f
9.1.4.13.
Answer.
  1. No
  2. 3 and 3.1; no
  3. 68. The two lines meet at \((20,68) \text{.}\)

Applications

9.1.4.15.
Answer.
b. \(m_{PQ}=\dfrac{-5}{2} \text{;}\) \(m_{PR}=\dfrac{2}{5} \)
9.1.4.17.
Answer.
  1. \(y=\dfrac{3}{2}x+\dfrac{5}{2}\text{;}\) the graph is below.
  2. \(\displaystyle \dfrac{3}{2}\)
  3. parallel lines
  4. \(\displaystyle y=\dfrac{3}{2}x+\dfrac{7}{2}\)
9.1.4.19.
Answer.
  1. \(\displaystyle y=-2x-8\)
  2. \(\displaystyle y=\dfrac{1}{2}x-3\)
9.1.4.21.
Answer.
\(y=\dfrac{3}{2}x+\dfrac{15}{2}\)

9.2 The Distance and Midpoint Formulas
9.2.7 Problem Set 9.2

Warm Up

9.2.7.1.
Answer.
  1. False
  2. False
9.2.7.3.
Answer.
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(y\) \(0\) \(\pm\sqrt{7}\) \(\pm\sqrt{12}\) \(\pm\sqrt{15}\) \(\pm 4\) \(\pm\sqrt{15}\) \(\pm\sqrt{12}\) \(\pm\sqrt{7}\) \(0\)
circle of radius 4 centered at origin
9.2.7.5.
Answer.
\(\dfrac{5\pm \sqrt{33}}{2} \)

Skills Practice

9.2.7.7.
Answer.
distance: \(\sqrt{20} \text{;}\) midpoint: \(\left(0,-2 \right) \)
9.2.7.9.
Answer.
distance: \(8\text{;}\) midpoint: \(\left(-2,-1 \right) \)
9.2.7.11.
Answer.
center: \((0,0) \text{;}\) radius: \(5 \)
9.2.7.13.
Answer.
center: \((-3,0) \text{;}\) radius: \(\sqrt{10} \)

Applications

9.2.7.15.
Answer.
\(15+\sqrt{80}+\sqrt{41} \approx 30.3\)
9.2.7.17.
Answer.
\(\sqrt{50} \approx 7.1\)
9.2.7.19.
Answer.
\(y=\dfrac{1}{2}x + \dfrac{5}{4}\)
9.2.7.21.
Answer.
  1. \(\displaystyle (220,-38.5)\)
  2. Both distances are 165.8 mi.
9.2.7.23.
Answer.
circle center at origin, radius 2
9.2.7.25.
Answer.
circle center at origin, radius 2
9.2.7.27.
Answer.
circle center at (0,-4) radius sqrt12
9.2.7.29.
Answer.
\((x+4)^2+y^2=20 \text{;}\) center: \((-4,0) \text{;}\) radius: \(\sqrt{20} \)
9.2.7.31.
Answer.
\(x^2+(y-5)^2=27 \text{;}\) center: \((0,5) \text{;}\) radius: \(\sqrt{27} \)
9.2.7.33.
Answer.
\(\left(x-\dfrac{3}{2}\right)^2+(y+4)^2=\dfrac{29}{4}\)
9.2.7.35.
Answer.
\(\left(x+3\right)^2+(y+1)^2=1\)

9.3 Conic Sections: Ellipses
9.3.5 Problem Set 9.3

Warm Up

9.3.5.1.
Answer.
  1. \(\displaystyle x^2+y^2=r^2\)
  2. \(\displaystyle \dfrac{x^2}{r^2}+\dfrac{y^2}{r^2}=1\)
  3. \(\displaystyle a=b=r\)
9.3.5.3.
Answer.
\((-2,6) \)
9.3.5.5.
Answer.
\(x\)-intercepts: \((-6,0)\text{,}\) \((4,0)\text{,}\) vertex: \(\left(-1,\dfrac{25}{2}\right)\)

Skills Practice

9.3.5.7.
Answer.
circle
9.3.5.9.
Answer.
central ellipse
9.3.5.11.
Answer.
central ellipse
9.3.5.13.
Answer.
  1. \(\displaystyle \dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
  2. \(x\) \(0\) \(\pm 3\) \(-2\) \(\dfrac{\pm 3\sqrt{3} }{2} \)
    \(y\) \(\pm 2\) \(0\) \(\dfrac{\pm 2\sqrt{5} }{2} \) \(1\)
9.3.5.15.
Answer.
  1. Radius 2
  2. \(\displaystyle (-1,\pm \sqrt{3})\)
9.3.5.17.
Answer.
  1. \(\displaystyle a=\sqrt{3},~b=\sqrt{6}\)
  2. None
9.3.5.19.
Answer.
  1. ellipse
  2. \((-1,4)\text{,}\) \((7,4)\text{,}\) \((3,1)\text{,}\) \((3,7)\) (Others are possible.)
9.3.5.21.
Answer.
  1. \(\displaystyle \dfrac{x^2}{4}+\dfrac{(y-2)^2}{9}=1\)
  2. ellipse
9.3.5.23.
Answer.
  1. \(\displaystyle \dfrac{(x-3)^2}{1}+\dfrac{(y+2)^2}{8}=1\)
  2. ellipse
9.3.5.25.
Answer.
\(\dfrac{(x-1)^2}{9}+\dfrac{(y-6)^2}{4}=1\)
9.3.5.27.
Answer.
\(\dfrac{(x-3)^2}{25}+\dfrac{(y-3)^2}{16}=1\)

Applications

9.3.5.29.
Answer.
  1. \(\displaystyle \dfrac{x^2}{10^2}+\dfrac{y^2}{7^2} = 1\)
  2. 4.2 ft
9.3.5.31.
Answer.
  1. \(\displaystyle \dfrac{x^2}{24^2}+\dfrac{y^2}{8^2} = 1\)
  2. 10.29 ft

9.4 Conic Sections: Hyperbolas
9.4.6 Problem Set 9.4

Skills Practice

9.4.6.3.
Answer.
hyperbola, open up and down
9.4.6.5.
Answer.
hyperbola, open left and right
9.4.6.7.
Answer.
hyperbola, open left and right
9.4.6.9.
Answer.
  1. \(\displaystyle \dfrac{x^2}{9} - \dfrac{y^2}{3} =1\)
  2. \(x\) \(0\) \(\dfrac{\pm3\sqrt{5}}{2} \) \(5\) \(\dfrac{\pm 15}{4} \)
    \(y\) undefined \(\pm 2\) \(\dfrac{\pm 16}{3} \) \(-3\)
9.4.6.11.
Answer.
  1. hyperbolas opening left and right
  2. hyperbolas opening left and right
9.4.6.13.
Answer.
  1. hyperbola opening up and down
  2. \(\left(-2, -2\pm \sqrt{6} \right) \text{,}\) \(\left(-2 \pm \sqrt{5} ,1\right) \)
9.4.6.15.
Answer.
  1. hyperbola opening up and down
  2. \(\left(1 -4\pm 2\sqrt{2} \right) \text{,}\) \((-2,-8) \text{,}\) \((4,-8)\)
9.4.6.17.
Answer.
  1. hyperbola opening up and down
  2. \(\left(3 \pm \sqrt{5} \right) \text{,}\) \(\left(3 \pm 2\sqrt{2}, 3 \right)\)
9.4.6.19.
Answer.
\(16x^2-y^2-192x-4y+556=0\)
9.4.6.21.
Answer.
\(x^2-4y^2+10x-16y-27=0\)
9.4.6.23.
Answer.
Parabola; vertex \((0,2)\text{,}\) opens downward, \(a=\dfrac{-1}{2} \)
9.4.6.25.
Answer.
Hyperbola; center \(\left(\dfrac{-1}{8},-1 \right) \text{,}\) transverse axis vertical, \(a^2=\dfrac{15}{65} \text{,}\) \(b^2=\dfrac{15}{16} \)
9.4.6.27.
Answer.
Parabola; vertex \((-4,2)\text{,}\) opens upward, \(a=\dfrac{1}{4} \)

Applications

9.4.6.29.
Answer.
520 ft
9.4.6.31.
Answer.
472.5 ft

9.5 Nonlinear Systems
9.5.4 Problem Set 9.5

Warm Up

9.5.4.1.
Answer.
\((1,-2)\)
9.5.4.3.
Answer.
\(x=3, 16\)

Skills Practice

9.5.4.5.
Answer.
\((-1, 12), (4, 7)\)
9.5.4.7.
Answer.
No solution
9.5.4.9.
Answer.
\((1, 4)\)
9.5.4.11.
Answer.
\((2,2) \text{,}\) \((-2,-2) \)
9.5.4.13.
Answer.
\((2,-1) \text{,}\) \((-2,1) \text{,}\) \((1,-2) \text{,}\) \((-1,2) \)
9.5.4.15.
Answer.
\((\pm 2,-\pm 5) \)
9.5.4.17.
Answer.
\((\pm 6,-\pm 2) \)
9.5.4.19.
Answer.
\((0,4) \text{,}\) \((-2,0) \)

Applications

9.5.4.21.
Answer.
12 ft by 18 ft
9.5.4.23.
Answer.
\(P=6\) lb per sq in; \(V=5\) cu. in.
9.5.4.25.
Answer.
  1. grid
  2. 1000 or 5000
  3. 2000 or 4000
  4. harvst 1800; stable population 3000
  5. extinction
9.5.4.27.
Answer.
  1. \(\displaystyle (200,~ 2600), (1400,~ 18,200)\)
  2. parabola and line
  3. \(\displaystyle x=800\)

9.6 Chapter 9 Summary and Review
9.6.3 Chapter 9 Review Problems

9.6.3.1.

Answer.
parallel

9.6.3.2.

Answer.
perpendicular

9.6.3.3.

Answer.
\(y=\dfrac{-2}{3}x+\dfrac{14}{3} \)

9.6.3.4.

Answer.
\(y=\dfrac{3}{2}x+\dfrac{5}{2} \)

9.6.3.5.

Answer.
\(y=\dfrac{2}{3}x-\dfrac{26}{3} \)

9.6.3.6.

Answer.
\(y=\dfrac{3}{2}x-2 \)

9.6.3.7.

Answer.
21.59; yes

9.6.3.8.

Answer.
10.8

9.6.3.9.

Answer.
circle

9.6.3.10.

Answer.
ellipse

9.6.3.11.

Answer.
ellipse

9.6.3.12.

Answer.
hyperbola

9.6.3.13.

Answer.
parabola

9.6.3.14.

Answer.
circle

9.6.3.15.

Answer.
ellipse

9.6.3.16.

Answer.
ellipse

9.6.3.17.

Answer.
hyperbola

9.6.3.18.

Answer.
parabola

9.6.3.19.

Answer.
  1. \(\displaystyle (x-2)^2+(y+1)^2=9\)
  2. Circle: center \((2,-1)\text{,}\) radius 3

9.6.3.20.

Answer.
  1. \(\displaystyle x^2+(y-3)^2=13\)
  2. Circle: center \((0,3)\text{,}\) radius \(\sqrt{13}\)

9.6.3.21.

Answer.
  1. \(\displaystyle \dfrac{(x-2)^2}{4}+\dfrac{(y+2)^2}{16}=1\)
  2. Ellipse: center \((2,-2)\text{,}\) \(a=2\text{,}\) \(b=4\)

9.6.3.22.

Answer.
  1. \(\displaystyle \dfrac{(x+1)^2}{5}+\dfrac{(y-2)^2}{8}=1\)
  2. Ellipse: center \((-1,2)\text{,}\) \(a=\sqrt{5}\text{,}\) \(b=\sqrt{8}\)

9.6.3.23.

Answer.
  1. \(\displaystyle y+10=(x-4)^2\)
  2. Parabola: vertex \((4,10)\text{,}\) opens upward, \(a=1\)

9.6.3.24.

Answer.
  1. \(\displaystyle x-2=\dfrac{-1}{4}(y+3)^2\)
  2. Parabola: vertex \((2,-3)\text{,}\) opens left, \(a=\dfrac{-1}{4}\)

9.6.3.25.

Answer.
  1. \(\displaystyle y+2=-(x-2)^2\)
  2. Parabola: vertex \((2,-2)\text{,}\) opens downward, \(a=-1\)

9.6.3.26.

Answer.
  1. \(\displaystyle x+\dfrac{3}{2}=\dfrac{1}{2}(y-1)^2\)
  2. Parabola: vertex \(\left(\dfrac{-3}{2},1\right)\text{,}\) opens right, \(a=\dfrac{1}{2}\)

9.6.3.27.

Answer.
  1. \(\displaystyle \dfrac{(y-4)^2}{6}-\dfrac{(x+2)^2}{4}=1\)
  2. Hyperbola: center \((-2,4)\text{,}\) transverse axis vertical, \(a=2\text{,}\) \(b=\sqrt{6}\)

9.6.3.28.

Answer.
  1. \(\displaystyle \dfrac{(x-4)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
  2. Hyperbola: center \((4,-3)\text{,}\) transverse axis horizontal, \(a=2\text{,}\) \(b=3\)

9.6.3.29.

Answer.
  1. \(\displaystyle \dfrac{x^2}{5}-\dfrac{(y-3)^2}{10}=1\)
  2. Hyperbola: center \((0,3)\text{,}\) transverse axis horizontal, \(a=\sqrt{5}\text{,}\) \(b=\sqrt{10}\)

9.6.3.30.

Answer.
  1. \(\displaystyle \dfrac{y^2}{3}-\dfrac{(x-4)^2}{12}=1\)
  2. Hyperbola: center \((4,0)\text{,}\) transverse axis vertical, \(a=2\sqrt{3}\text{,}\) \(b=\sqrt{310}\)

9.6.3.31.

Answer.
  1. \(\displaystyle \dfrac{x^2}{25}+\dfrac{y^2}{64}=1\)
  2. \(\displaystyle \dfrac{\pm 24}{5}\)

9.6.3.32.

Answer.
  1. \(\displaystyle \dfrac{x^2}{169}+\dfrac{y^2}{81}=1\)
  2. \(\displaystyle \dfrac{\pm 45}{13}\)

9.6.3.33.

Answer.
\((x+4)^2+(y-3)^2=20 \)

9.6.3.34.

Answer.
\((x+2)^2+(y-4)^2=13 \)

9.6.3.35.

Answer.
\(\dfrac{(x+1)^2}{16}+\dfrac{(y-4)^2}{4}=1 \)

9.6.3.36.

Answer.
\(\dfrac{(x-3)^2}{4}+\dfrac{(y-1)^2}{25}=1 \)

9.6.3.37.

Answer.
\(\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1 \)

9.6.3.38.

Answer.
\((x+3)^2 -\dfrac{(y-1)^2}{9}=1 \)

9.6.3.39.

Answer.
\((\pm 2, \pm 3) \)

9.6.3.40.

Answer.
\((\pm\sqrt{3}, \pm 4) \)

9.6.3.41.

Answer.
\((1,-2) \text{,}\) \((-1,2) \text{,}\) \(\left(2\sqrt{3}, \dfrac{-1}{\sqrt{3}} \right) \text{,}\) \(\left(-2\sqrt{3}, \dfrac{1}{\sqrt{3}} \right) \)

9.6.3.42.

Answer.
\(\left(\dfrac{\sqrt{34}}{2}, \dfrac{\sqrt{34}}{2} \right) \text{,}\) \(\left(\dfrac{-\sqrt{34}}{2}, \dfrac{-\sqrt{34}}{2} \right) \)

9.6.3.43.

Answer.
Moia: 45 mph, Fran: 50 mph

9.6.3.44.

Answer.
12 in by 1 in

9.6.3.45.

Answer.
7 cm by 10 cm

9.6.3.46.

Answer.
7 ft by 2 ft

9.6.3.47.

Answer.
Morning train: 20 mph, evening train: 30 mph

9.6.3.48.

Answer.
Amount: $800, rate: 4%

10 Logarithmic Functions
10.1 Logarithmic Functions
10.1.6 Problem Set 10.1

Warm Up

10.1.6.1.
Answer.
\(9^y=729\)
10.1.6.3.
Answer.
\(10^{-4.5}=C\)
10.1.6.5.
Answer.
\(\log_b{\dfrac{1}{4}}\)
10.1.6.7.
Answer.
\(\log_{10}{\sqrt{\dfrac{xy}{z^3}}}\)

Skills Practice

10.1.6.9.
Answer.
3 to x and log base 3
10.1.6.11.
Answer.
  1. \(\displaystyle 15.6144\)
  2. \(\displaystyle 0.4186\)
10.1.6.13.
Answer.
\(-1.58 \times 10^{-5}\)
10.1.6.15.
Answer.
  1. \(\displaystyle 25.70\)
  2. \(\displaystyle 3.31\)
10.1.6.17.
Answer.
  1. \(\displaystyle \dfrac{1}{2}\)
  2. \(\displaystyle 01\)
10.1.6.19.
Answer.
  1. 81
  2. 4
  3. 1.8
  4. \(\displaystyle a\)
10.1.6.21.
Answer.
  1. IV
  2. V
  3. I
  4. II
  5. III
  6. VI
10.1.6.23.
Answer.
  1. 10,000
  2. 100,000,000
10.1.6.25.
Answer.
\(4\)
10.1.6.27.
Answer.
3

Applications

10.1.6.29.
Answer.
  1. data points and log curve
  2. The graph resembles a logarithmic function. The function is close to the points but appears too steep at first and not steep enough after \(n = 15\text{.}\) Overall, it is a good fit.
  3. \(f\) grows (more and more slowly) without bound. \(f\) will eventually exceed \(100\) per cent, but no one can forget more than 100% of what is learned.
10.1.6.31.
Answer.
1962

10.2 Logarithmic Scales
10.2.6 Problem Set 10.2

Warm Up

10.2.6.1.
Answer.
  1. 0 and 1
  2. 2 and 3
  3. \(-1\) and 0
  4. 6 and 7
10.2.6.3.
Answer.
  1. 3981.1
  2. 5.01
  3. 0.00079
  4. 0.398

Skills Practice

10.2.6.5.
Answer.
  1. log scale with exponents shown
  2. log scale with exponents shown
10.2.6.7.
Answer.
logscale
10.2.6.9.
Answer.
\(1.58\text{,}\) \(6.31\text{,}\) \(15.8\text{,}\) \(63.1\)
10.2.6.11.
Answer.
\(3.2\)
10.2.6.13.
Answer.
\(0.0126\)
10.2.6.15.
Answer.
\(100\)
10.2.6.17.
Answer.
6,309,573 watts per square meter

Applications

10.2.6.19.
Answer.
\(1\text{,}\) \(80\text{,}\) \(330\text{,}\) \(1600\text{,}\) \(7000\text{,}\) \(4\times 10^7\)
10.2.6.21.
Answer.
Proxima Centauri: \(15.5\text{;}\) Barnard: \(13.2\text{;}\) Sirius: \(1.4\text{;}\) Vega: \(0.6\text{;}\) Arcturus: \(-0.4\text{;}\) Antares: \(-4.7\text{;}\) Betelgeuse: \(-7.2\)
10.2.6.23.
Answer.
pH on log scale
10.2.6.25.
Answer.
\(10^{3.4} \approx 2512\)
10.2.6.27.
Answer.
A: \(a\approx 45\text{,}\) \(p \approx 7.4\%\text{;}\) B: \(a \approx 400\text{,}\) \(p \approx 15\%\text{;}\) C: \(a\approx 6000\text{,}\) \(p\approx 50\%\text{;}\) D: \(a \approx 13000\text{,}\) \(p \approx 45\%\)
10.2.6.29.
Answer.
12.6
10.2.6.32.
Answer.
\(3160\)
10.2.6.33.
Answer.
\(\approx 25,000\)

10.3 The Natural Base
10.3.6 Homework 10.3

Skills Practice

10.3.6.1.
Answer.
\(x\) \(-10\) \(-5\) \(0\) \(5\) \(10\) \(15\) \(20\)
\(f(x)\) \(0.135\) \(0.368\) \(1\) \(2.718\) \(7.389\) \(20.086\) \(54.598\)
growth
10.3.6.3.
Answer.
\(x\) \(-10\) \(-5\) \(0\) \(5\) \(10\) \(15\) \(20\)
\(f(x)\) \(20.086\) \(4.482\) \(1\) \(0.223\) \(0.05\) \(0.011\) \(0.00248\)
decay
10.3.6.5.
Answer.
  1. \(\displaystyle 2\)
  2. \(\displaystyle 5t\)
  3. \(\displaystyle \dfrac{1}{x} \)
  4. \(\displaystyle \dfrac{1}{2} \)
10.3.6.7.
Answer.
  1. \(\displaystyle 0.64\)
  2. \(\displaystyle 3.81\)
  3. \(\displaystyle -1.20\)
10.3.6.9.
Answer.
  1. \(\displaystyle 4.14\)
  2. \(\displaystyle 1.88\)
  3. \(\displaystyle 0.07\)
10.3.6.11.
Answer.
\(P (t) = 20\left(e^{0.4} \right)^t \approx 20\cdot 1.492^t\text{;}\) increasing; initial value \(20\)
10.3.6.13.
Answer.
\(P (t) = 6500\left(e^{-2.5} \right)^t \approx 6500\cdot 0.082^t\text{;}\) decreasing; initial value \(6500\)
10.3.6.15.
Answer.
  1. \(x\) \(0\) \(0.5\) \(1\) \(1.5\) \(2\) \(2.5\)
    \(e^x\) \(1 \) \(1.6487\) \(2.7183\) \(4.4817\) \(7.3891\) \(12.1825\)
  2. Each ratio is \(e^{0.5} \approx 1.6487\text{:}\) Increasing \(x\)-values by a constant \(\Delta x = 0.5\) corresponds to multiplying the \(y\)-values of the exponential function by a constant factor of \(e^{\Delta x}\text{.}\)
10.3.6.17.
Answer.
  1. \(x\) \(0\) \(0.6931\) \(1.3863\) \(2.0794\) \(2.7726\) \(3.4657\) \(4.1589\)
    \(e^x\) \(1 \) \(2\) \(4\) \(8\) \(16\) \(32\) \(64\)
  2. Each difference in \(x\)-values is approximately \(\ln 2\approx 0.6931\text{:}\) Increasing \(x\)-values by a constant \(\Delta x = \ln 2\) corresponds to multiplying the \(y\)-values of the exponential function by a constant factor of \(e^{\Delta x} = e^{\ln 2} = 2\text{.}\) That is, each function value is approximately equal to double the previous one.
10.3.6.19.
Answer.
\(0.8277\)
10.3.6.21.
Answer.
\(-2.9720\)
10.3.6.23.
Answer.
\(1.6451\)
10.3.6.25.
Answer.
\(-3.0713\)
10.3.6.27.
Answer.
\(t=\dfrac{1}{k}\ln y \)
10.3.6.29.
Answer.
\(t=\ln \left(\dfrac{k}{k-y}\right) \)
10.3.6.31.
Answer.
\(k=e^{T/T_0}-10 \)
10.3.6.33.
Answer.
  1. \(n\) \(0.39\) \(3.9\) \(39\) \(390\)
    \(\ln n\) \(-0.942 \) \(1.361 \) \(3.664 \) \(5.966 \)
  2. Each difference in function values is approximately \(\ln 10\approx 2.303\text{:}\) Multiplying \(x\)-values by a constant factor of 10 corresponds to adding a constant value of \(\ln 10\) to the \(y\)-values of the natural log function.
10.3.6.35.
Answer.
  1. \(n\) \(2\) \(4\) \(8\) \(16\)
    \(\ln n\) \(0.693 \) \(1.386 \) \(2.079 \) \(2.773 \)
  2. Each quotient equals \(k\text{,}\) where \(n = 2^k\text{.}\) Because \(\ln n = \ln 2^k = k\cdot \ln 2\text{,}\) \(k = \dfrac{\ln n}{\ln 2}\text{.}\)
10.3.6.37.
Answer.
  1. \(\displaystyle N (t) = 100e^{(\ln 2)t}\approx 100e^{0.6931t}\)
  2. growth
10.3.6.39.
Answer.
  1. \(\displaystyle N (t) = 1200e^{(\ln 0.6)t}\approx 1200e^{-0.5108t}\)
  2. decay
10.3.6.41.
Answer.
  1. \(\displaystyle N (t) = 10e^{(\ln 1.15)t}\approx 10e^{0.1398t}\)
  2. growth

Applications

10.3.6.43.
Answer.
  1. \(\displaystyle N(t)=6000e^{0.04t} \)
  2. \(t\) \(0\) \(5\) \(10\) \(15\) \(20\) \(25\) \(30\)
    \(N(t)\) \(6000\) \(7328\) \(8951\) \(10,933\) \(13,353\) \(16,310\) \(19,921\)
  3. growth
  4. 15,670
  5. 70.3 hrs
10.3.6.45.
Answer.
  1. decay
  2. 941.8 lumens
  3. 2.2 cm
10.3.6.47.
Answer.
  1. 20,000
  2. \(\displaystyle \left(\dfrac{35,000}{20,000} \right)^{1/10}\approx e^{0.056} \)
  3. \(\displaystyle P(t) = 20,000e^{0.056t} \)
  4. 107,188
10.3.6.49.
Answer.
  1. \(\displaystyle \left(\dfrac{385}{500} \right)^{1/2}\approx e^{-0.1307} \)
  2. \(\displaystyle N(t) = 500e^{-0.1307t} \)
  3. 135.3 mg
10.3.6.51.
Answer.
  1. \(\displaystyle A(t) = 500e^{0.095t}\)
  2. 7.3 years
  3. 7.3 years
d–e
growth with marked doubling time
10.3.6.53.
Answer.
  1. 6 hours
  2. 6 hours
  3. decay with marked half-life
10.3.6.55.
Answer.
  1. \(\frac{1}{2}N_0 \text{,}\) \(\frac{1}{4}N_0 \text{,}\) \(\frac{1}{16}N_0\)
  2. decay
  3. \(\displaystyle N (t) = N_0e^{-0.0866t}\)
10.3.6.57.
Answer.
  1. decay fit on data
    \(\displaystyle y = 116 (0.975)^t\)
  2. \(\displaystyle G (t) = 116e^{-0.025t}\)
  3. 28 minutes

10.4 Chapter 10 Summary and Review
10.4.3 Chapter 10 Review Problems

10.4.3.5.

Answer.
\(-1\)

10.4.3.7.

Answer.
\(\dfrac{1}{2} \)

10.4.3.9.

Answer.
\(4 \)

10.4.3.11.

Answer.
\(\dfrac{-15}{8} \)

10.4.3.13.

Answer.
\(\dfrac{9}{4} \)

10.4.3.15.

Answer.
\(3 \)

10.4.3.17.

Answer.
\(x\approx 1.548 \)

10.4.3.19.

Answer.
\(x\approx 411.58 \)

10.4.3.21.

Answer.
\(x\approx 2.286 \)

10.4.3.23.

Answer.
\(\sqrt{x} \)

10.4.3.25.

Answer.
\(k-3 \)

10.4.3.27.

Answer.
  1. \(\displaystyle P = 7,894,862e^{-0.011t}\)
  2. 1.095%

10.4.3.29.

Answer.
  1. $1419.07
  2. 13.9 years
  3. \(\displaystyle t = 20 \ln\left(\dfrac{A}{1000} \right)\)

10.4.3.31.

Answer.
\(t=\dfrac{-1}{k}\ln\left(\dfrac{y-6}{12} \right) \)

10.4.3.33.

Answer.
\(M=N^{Qt} \)

10.4.3.35.

Answer.
\(P (t) = 750 (1.3771)^t\)

10.4.3.37.

Answer.
\(N(t) = 600 e^{-0.9163t}\)

10.4.3.39.

Answer.
log scale

10.4.3.41.

Answer.
Order 3: 17,000; Order 4: 5000; Order 8: 40; Order 9: 11
PrevTopNext