6.8. Tree Traversals¶
Now that we have examined the basic functionality of our tree data structure, it is time to look at some additional usage patterns for trees. These usage patterns can be divided into three commonly used patterns to visit all the nodes in a tree. The difference between these patterns is the order in which each node is visited. We call this visitation of the nodes a tree traversal. The three traversals we will look at are called preorder, inorder, and postorder. Let’s start out by defining these three traversals more carefully, then look at some examples where these patterns are useful.
- Preorder
In a preorder traversal, we visit the root node first, then recursively do a preorder traversal of the left subtree, followed by a recursive preorder traversal of the right subtree.
- Inorder
In an inorder traversal, we recursively do an inorder traversal on the left subtree, visit the root node, and finally do a recursive inorder traversal of the right subtree.
- Postorder
In a postorder traversal, we recursively do a postorder traversal of the left subtree and the right subtree followed by a visit to the root node.
Let’s look at some examples that illustrate each of these three kinds of traversals. First let’s look at the preorder traversal using a book as an example tree. The book is the root of the tree, and each chapter is a child of the root. Each section within a chapter is a child of the chapter, each subsection is a child of its section, and so on. Figure 5 shows a limited version of a book with only two chapters. Note that the traversal algorithm works for trees with any number of children, but we will stick with binary trees for now.
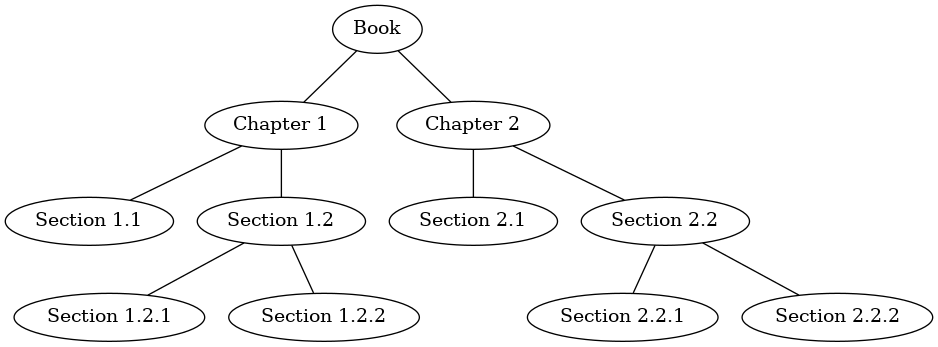
Figure 5: Representing a Book as a Tree¶
Suppose that you wanted to read this book from front to back. The
preorder traversal gives you exactly that ordering. Starting at the root
of the tree (the Book node) we will follow the preorder traversal
instructions. We recursively call preorder on the left child, in
this case Chapter1. We again recursively call preorder on the left
child to get to Section 1.1. Since Section 1.1 has no children, we do
not make any additional recursive calls. When we are finished with
Section 1.1, we move up the tree to Chapter 1. At this point we still
need to visit the right subtree of Chapter 1, which is Section 1.2. As
before we visit the left subtree, which brings us to Section 1.2.1, then
we visit the node for Section 1.2.2. With Section 1.2 finished, we
return to Chapter 1. Then we return to the Book node and follow the same
procedure for Chapter 2.
The code for writing tree traversals is surprisingly elegant, largely
because the traversals are written recursively. You may wonder,
what is the best way to write an algorithm like preorder
traversal? Should it be a function that simply uses a tree as a data
structure, or should it be a method of the tree data structure itself?
Listing 2 shows a version of the preorder traversal
written as an external function that takes a binary tree as a parameter.
The external function is particularly elegant because our base case is
simply to check if the tree exists. If the tree parameter is None,
then the function returns without taking any action.
Listing 2
def preorder(tree):
if tree:
print(tree.key)
preorder(tree.left_child)
preorder(tree.right_child)
We can also implement preorder as a method of the BinaryTree
class. The code for implementing preorder as an internal method is
shown in Listing 3. Notice what happens when we move the
code from external to internal. In general, we just replace tree
with self. However, we also need to modify the base case. The
internal method must check for the existence of the left and the right
children before making the recursive call to preorder.
Listing 3
def preorder(self):
print(self.key)
if self.left_child:
self.left_child.preorder()
if self.right_child:
self.right_child.preorder()
Which of these two ways to implement preorder is best? The answer is
that implementing preorder as an external function is probably
better in this case. The reason is that you very rarely want to just
traverse the tree. In most cases you are going to want to accomplish
something else while using one of the basic traversal patterns. In fact,
we will see in the next example that the postorder traversal pattern
follows very closely with the code we wrote earlier to evaluate a parse
tree. Therefore we will write the rest of the traversals as external
functions.
The algorithm for the postorder traversal, shown in
Listing 4, is nearly identical to preorder except that
we move the call to print to the end of the function.
Listing 4
def postorder(tree):
if tree:
postorder(tree.left_child)
postorder(tree.right_child)
print(tree.key)
We have already seen a common use for the postorder traversal, namely evaluating a parse tree. Look back at Listing 1 again. The algorithm evaluates the left subtree, evaluates the right subtree, and combines them in the root through the function call to an operator. Assuming our binary tree is going to store only expression tree data, rewrite the evaluation function, but model it even more closely on the postorder code in Listing 4.
Listing 5
def postordereval(tree):
operators = {
"+": operator.add,
"-": operator.sub,
"*": operator.mul,
"/": operator.truediv,
}
result_1 = None
result_2 = None
if tree:
result_1 = postordereval(tree.left_child)
result_2 = postordereval(tree.right_child)
if result_1 and result_2:
return operators[tree.key](result_1, result_2)
return tree.key
Notice that the form in Listing 4 is the same as the form in Listing 5, except that instead of printing the key at the end of the function, we return it. This allows us to save the values returned from the recursive calls in lines 11 and 12. We then use these saved values along with the operator on line 14.
The final traversal we will look at in this section is the inorder
traversal. In the inorder traversal we visit the left subtree, followed
by the root, and finally the right subtree. Listing 6 shows
our code for the inorder traversal. Notice that in all three of the
traversal functions we are simply changing the position of the print
function with respect to the two recursive function calls.
Listing 6
def inorder(tree):
if tree:
inorder(tree.left_child)
print(tree.key)
inorder(tree.right_child)
If we perform a simple inorder traversal of a parse tree, we get our original expression back without any parentheses. Let’s modify the basic inorder algorithm to allow us to recover the fully parenthesized version of the expression. The only modifications we will make to the basic template are as follows: print a left parenthesis before the recursive call to the left subtree, and print a right parenthesis after the recursive call to the right subtree. The modified code is shown in Listing 7.
Listing 7
def print_exp(tree):
result = ""
if tree:
result = "(" + print_exp(tree.left_child)
result = result + str(tree.key)
result = result + print_exp(tree.right_child) + ")"
return result
Notice that the print_exp function as we have implemented it puts
parentheses around each number. While not incorrect, the parentheses are
clearly not needed. In the exercises at the end of this chapter you are
asked to modify the print_exp function to remove this set of parentheses.