6.22. Exercises¶
Draw the tree structure resulting from the following set of tree function calls:
>>> r = BinaryTree(3) >>> insert_left(r, 4) [3, [4, [], []], []] >>> insert_left(r, 5) [3, [5, [4, [], []], []], []] >>> insert_right(r, 6) [3, [5, [4, [], []], []], [6, [], []]] >>> insert_right(r, 7) [3, [5, [4, [], []], []], [7, [], [6, [], []]]] >>> set_root_val(r, 9) >>> insert_left(r, 11) [9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]
Trace the algorithm for creating an expression tree for the expression \((4 * 8) / 6 - 3\).
Consider the following list of integers: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Show the binary search tree resulting from inserting the integers in the list.
Consider the following list of integers: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. Show the binary search tree resulting from inserting the integers in the list.
Generate a random list of integers. Show the binary heap tree resulting from inserting the integers on the list one at a time.
Using the list from the previous question, show the binary heap tree resulting from using the list as a parameter to the
heapifymethod. Show both the tree and list form.Draw the binary search tree that results from inserting the following keys in the order given: 68, 88, 61, 89, 94, 50, 4, 76, 66, and 82.
Generate a random list of integers. Draw the binary search tree resulting from inserting the integers on the list.
Consider the following list of integers: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Show the binary heap resulting from inserting the integers one at a time.
Consider the following list of integers: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. Show the binary heap resulting from inserting the integers one at a time.
Consider the two different techniques we used for implementing traversals of a binary tree. Why must we check before the call to
preorderwhen implementing it as a method, whereas we could check inside the call when implementing it as a function?Show the function calls needed to build the following binary tree.
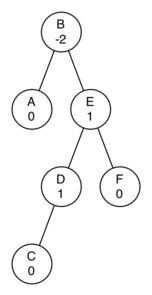
Given the following tree, perform the appropriate rotations to bring it back into balance.
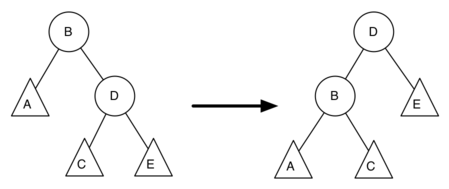
Using the following as a starting point, derive the equation that gives the updated balance factor for node D.
Extend the
build_parse_treefunction to handle mathematical expressions that do not have spaces between every character.Modify the
build_parse_treeandevaluatefunctions to handle Boolean statements (and,or, andnot). Remember thatnotis a unary operator, so this will complicate your code somewhat.Using the
find_successormethod, write a non-recursive inorder traversal for a binary search tree.A threaded binary tree maintains a reference from each node to its successor. Modify the code for a binary search tree to make it threaded, then write a non-recursive inorder traversal method for the threaded binary search tree.
Modify our implementation of the binary search tree so that it handles duplicate keys properly. That is, if a key is already in the tree then the new payload should replace the old rather than add another node with the same key.
Create a binary heap with a limited heap size. In other words, the heap only keeps track of the \(n\) most important items. If the heap grows in size to more than \(n\) items the least important item is dropped.
Clean up the
print_expfunction so that it does not include an extra set of parentheses around each number.Using the
heapifymethod, write a sorting function that can sort a list in \(O(n\log{n})\) time.Write a function that takes a parse tree for a mathematical expression and calculates the derivative of the expression with respect to some variable.
Implement a binary heap as a max heap.
Using the
BinaryHeapclass, implement a new class calledPriorityQueue. YourPriorityQueueclass should implement the constructor plus theenqueueanddequeuemethods.Implement the
deletemethod for an AVL tree.