6.14. Search Tree Implementation¶
A binary search tree (BST) relies on the property that
keys that are less than the parent are found in the left subtree, and
keys that are greater than the parent are found in the right subtree. We
will call this the BST property. As we implement the Map interface
as described above, the BST property will guide our implementation.
Figure 1 illustrates this property of a binary search
tree, showing the keys without any associated values. Notice that the
property holds for each parent and child. All of the keys in the left
subtree are less than the key in the root. All of the keys in the right
subtree are greater than the root.
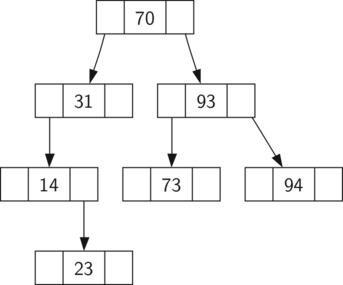
Figure 1: A Simple Binary Search Tree¶
Now that you know what a binary search tree is, we will look at how a binary search tree is constructed. The search tree in Figure 1 represents the nodes that exist after we have inserted the following keys in the order shown: \(70, 31, 93, 94, 14, 23, 73\). Since 70 was the first key inserted into the tree, it is the root. Next, 31 is less than 70, so it becomes the left child of 70. Next, 93 is greater than 70, so it becomes the right child of 70. Now we have two levels of the tree filled, so the next key is going to be the left or right child of either 31 or 93. Since 94 is greater than 70 and 93, it becomes the right child of 93. Similarly 14 is less than 70 and 31, so it becomes the left child of 31. 23 is also less than 31, so it must be in the left subtree of 31. However, it is greater than 14, so it becomes the right child of 14.
To implement the binary search tree, we will use the nodes and
references approach similar to the one we used to implement the linked
list and the expression tree. However, because we must be able create
and work with a binary search tree that is empty, our implementation
will use two classes. The first class we will call BinarySearchTree,
and the second class we will call TreeNode. The BinarySearchTree
class has a reference to the TreeNode that is the root of the binary
search tree. In most cases the external methods defined in the outer
class simply check to see if the tree is empty. If there are nodes in
the tree, the request is just passed on to a private method defined in
the BinarySearchTree class that takes the root as a parameter. In
the case where the tree is empty or we want to delete the key at the
root of the tree, we must take special action. The code for the
BinarySearchTree class constructor along with a few other
miscellaneous methods is shown in Listing 1.
Listing 1
class BinarySearchTree:
def __init__(self):
self.root = None
self.size = 0
def __len__(self):
return self.size
def __iter__(self):
return self.root.__iter__()
The TreeNode class provides many helper methods that make the work
done in the BinarySearchTree class methods much easier. The
constructor for a TreeNode, along with these helper methods, is
shown in Listing 2. As you can see in the listing many of
these helper methods help to classify a node according to its own
position as a child (left or right) and the kind of children the node
has.
The TreeNode class will also explicitly keep track
of the parent as an attribute of each node. You will see why this is
important when we discuss the implementation for the del operator.
Another interesting aspect of the implementation of TreeNode in
Listing 2 is that we use Python’s optional parameters.
Optional parameters make it easy for us to create a TreeNode under
several different circumstances. Sometimes we will want to construct a
new TreeNode that already has both a parent and a child (e.g. left) and
in that case we can pass parent and left_child as
parameters. At other times we will just create a TreeNode with the
key-value pair, and we will not pass any parameters for parent or
child. In this case, the default values of the optional parameters
are used.
Listing 2
class TreeNode:
def __init__(self, key, value, left=None, right=None, parent=None):
self.key = key
self.value = value
self.left_child = left
self.right_child = right
self.parent = parent
def is_left_child(self):
return self.parent and self.parent.left_child is self
def is_right_child(self):
return self.parent and self.parent.right_child is self
def is_root(self):
return not self.parent
def is_leaf(self):
return not (self.right_child or self.left_child)
def has_any_child(self):
return self.right_child or self.left_child
def has_children(self):
return self.right_child and self.left_child
def replace_value(self, key, value, left, right):
self.key = key
self.value = value
self.left_child = left
self.right_child = right
if self.left_child:
self.left_child.parent = self
if self.right_child:
self.right_child.parent = self
Now that we have the BinarySearchTree shell and the TreeNode, it
is time to write the put method that will allow us to build our
binary search tree. The put method is a method of the
BinarySearchTree class. This method will check to see if the tree
already has a root. If there is not a root, then put will create a
new TreeNode and install it as the root of the tree. If a root node
is already in place, then put calls the private recursive helper
method _put to search the tree according to the following
algorithm:
Starting at the root of the tree, search the binary tree comparing the new key to the key in the current node. If the new key is less than the current node, search the left subtree. If the new key is greater than the current node, search the right subtree.
When there is no left or right child to search, we have found the position in the tree where the new node should be installed.
To add a node to the tree, create a new
TreeNodeobject and insert the object at the point discovered in the previous step.
Listing 3 shows the Python code for inserting a new node in
the tree. The _put method is written recursively following the
steps outlined above. Notice that when a new child is inserted into the
tree, the current_node is passed to the new tree as the parent.
One important problem with our implementation of insertion is that duplicate keys are not handled properly. As our tree is implemented, a duplicate key will create a new node with the same key value in the right subtree of the node having the original key. The result of this is that the node with the new key will never be found during a search. A better way to handle the insertion of a duplicate key is for the value associated with the new key to replace the old value. We leave fixing this bug as an exercise for you.
Listing 3
def put(self, key, value):
if self.root:
self._put(key, value, self.root)
else:
self.root = TreeNode(key, value)
self.size = self.size + 1
def _put(self, key, value, current_node):
if key < current_node.key:
if current_node.left_child:
self._put(key, value, current_node.left_child)
else:
current_node.left_child = TreeNode(key, value, parent=current_node)
else:
if current_node.right_child:
self._put(key, value, current_node.right_child)
else:
current_node.right_child = TreeNode(key, value, parent=current_node)
With the put method defined, we can easily overload the []
operator for assignment by having the __setitem__ method call the
put method (see Listing 4). This allows us to write Python statements like
my_zip_tree['Plymouth'] = 55446, just like a Python dictionary.
Listing 4
def __setitem__(self, key, value):
self.put(key, value)
Figure 2 illustrates the process for inserting a new node into a binary search tree. The lightly shaded nodes indicate the nodes that were visited during the insertion process.
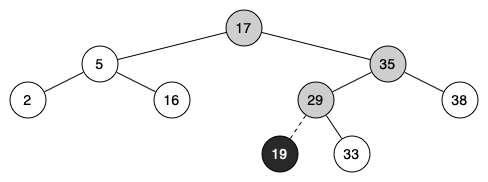
Figure 2: Inserting a Node with Key = 19¶
Self Check

- Remember, starting at the root keys less than the root must be in the left subtree, while keys greater than the root go in the right subtree.

- good job.

- This looks like a binary tree that satisfies the full tree property needed for a heap.
Q-1: Which of the trees shows a correct binary search tree given that the keys were inserted in the following order 5, 30, 2, 40, 25, 4.
Once the tree is constructed, the next task is to implement the
retrieval of a value for a given key. The get method is even easier
than the put method because it simply searches the tree recursively
until it gets to a non-matching leaf node or finds a matching key. When
a matching key is found, the value stored in the payload of the node is
returned.
Listing 5 shows the code for get and _get.
The search code in the _get method uses the same
logic for choosing the left or right child as the _put method. Notice
that the _get method returns a TreeNode to get, this allows
_get to be used as a flexible helper method for other
BinarySearchTree methods that may need to make use of other data
from the TreeNode besides the payload.
Listing 5
def get(self, key):
if self.root:
result = self._get(key, self.root)
if result:
return result.value
return None
def _get(self, key, current_node):
if not current_node:
return None
if current_node.key == key:
return current_node
elif key < current_node.key:
return self._get(key, current_node.left_child)
else:
return self._get(key, current_node.right_child)
By implementing the __getitem__ method we can write a Python
statement that looks just like we are accessing a dictionary, when in
fact we are using a binary search tree, for example
z = my_zip_tree["Fargo"]. As you can see in Listing 6,
all the __getitem__ method does is call get.
Listing 6
def __getitem__(self, key):
return self.get(key)
Using get, we can implement the in operation by writing a
__contains__ method for the BinarySearchTree. The
__contains__ method will simply call get and return True
if get returns a value, or False if it returns None. The
code for __contains__ is shown in Listing 7.
Listing 7
def __contains__(self, key):
return bool(self._get(key, self.root))
Recall that __contains__ overloads the in operator and allows us
to write statements such as "Northfield" in my_zip_tree.
Finally, we turn our attention to the most challenging operation on the
binary search tree, the deletion of a key (see Listing 8).
The first task is to find the
node to delete by searching the tree. If the tree has more than one node
we search using the _get method to find the TreeNode that needs
to be removed. If the tree only has a single node, that means we are
removing the root of the tree, but we still must check to make sure the
key of the root matches the key that is to be deleted. In either case if
the key is not found the del operator raises an error.
Listing 8
def delete(self, key):
if self.size > 1:
node_to_remove = self._get(key, self.root)
if node_to_remove:
self._delete(node_to_remove)
self.size = self.size - 1
else:
raise KeyError("Error, key not in tree")
elif self.size == 1 and self.root.key == key:
self.root = None
self.size = self.size - 1
else:
raise KeyError("Error, key not in tree")
Once we’ve found the node containing the key we want to delete, there are three cases that we must consider:
The node to be deleted has no children (see Figure 3).
The node to be deleted has only one child (see Figure 4).
The node to be deleted has two children (see Figure 5).
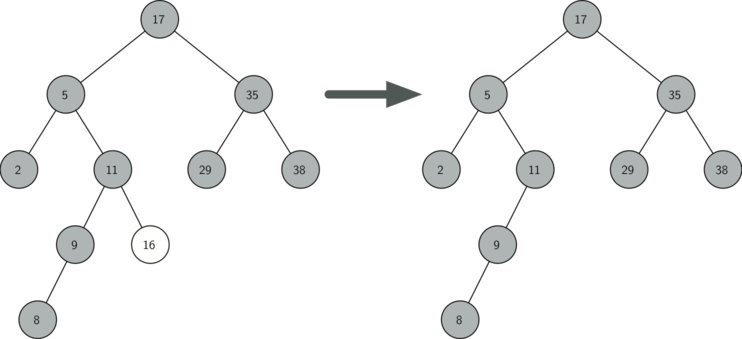
Figure 3: Deleting Node 16, a Node without Children¶
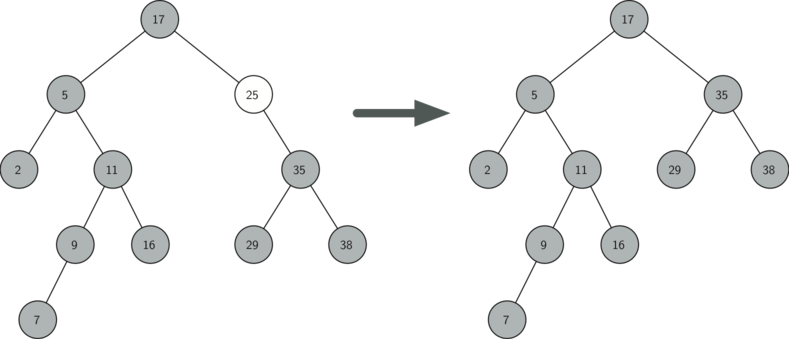
Figure 4: Deleting Node 25, a Node That Has a Single Child¶
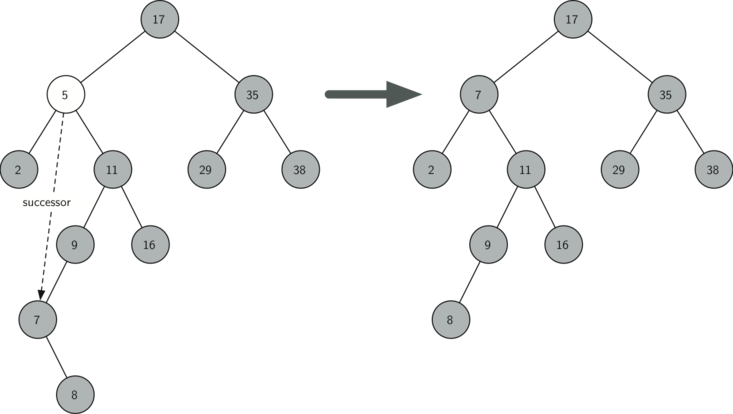
Figure 5: Deleting Node 5, a Node with Two Children¶
The first case is straightforward. If the current node has no children, all we need to do is delete the node and remove the reference to this node in the parent. The code for this case is shown in Listing 9.
Listing 9
if current_node.is_leaf():
if current_node == current_node.parent.left_child:
current_node.parent.left_child = None
else:
current_node.parent.right_child = None
The second case is only slightly more complicated. If a node has only a single child, then we can simply promote the child to take the place of its parent. The code for this case is shown in Listing 10. As you look at this code, you will see that there are six cases to consider. Since the cases are symmetric with respect to either having a left or right child, we will just discuss the case where the current node has a left child. The decision proceeds as follows:
If the current node is a left child, then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the left child reference of the parent to point to the current node’s left child.
If the current node is a right child, then we only need to update the parent reference of the left child to point to the parent of the current node, and then update the right child reference of the parent to point to the current node’s left child.
If the current node has no parent, it must be the root. In this case we will just replace the
key,value,left_child, andright_childdata by calling thereplace_valuemethod on the root.
Listing 10
else: # removing a node with one child
if current_node.get_left_child():
if current_node.is_left_child():
current_node.left_child.parent = current_node.parent
current_node.parent.left_child = current_node.left_child
elif current_node.is_right_child():
current_node.left_child.parent = current_node.parent
current_node.parent.right_child = current_node.left_child
else:
current_node.replace_value(
current_node.left_child.key,
current_node.left_child.value,
current_node.left_child.left_child,
current_node.left_child.right_child,
)
else:
if current_node.is_left_child():
current_node.right_child.parent = current_node.parent
current_node.parent.left_child = current_node.right_child
elif current_node.is_right_child():
current_node.right_child.parent = current_node.parent
current_node.parent.right_child = current_node.right_child
else:
current_node.replace_value(
current_node.right_child.key,
current_node.right_child.value,
current_node.right_child.left_child,
current_node.right_child.right_child,
)
The third case is the most difficult case to handle. If a node has two children, then it is unlikely that we can simply promote one of them to take the node’s place. We can, however, search the tree for a node that can be used to replace the one scheduled for deletion. What we need is a node that will preserve the binary search tree relationships for both of the existing left and right subtrees. The node that will do this is the node that has the next-largest key in the tree. We call this node the successor, and we will look at a way to find the successor shortly. The successor is guaranteed to have no more than one child, so we know how to remove it using the two cases for deletion that we have already implemented. Once the successor has been removed, we simply put it in the tree in place of the node to be deleted. The code to handle the third case is shown in Listing 11.
In Listing 11 we make use of the helper methods
find_successor and splice_out to find and remove the successor.
The reason we use splice_out is that it
goes directly to the node we want to splice out and makes the right
changes. We could call delete recursively, but then we would waste
time searching again for the key node.
Listing 11
elif current_node.has_children(): # removing a node with two children
successor = current_node.find_successor()
successor.splice_out()
current_node.key = successor.key
current_node.value = successor.value
The code to find the successor is shown below (see Listing 12) and as
you can see is a method of the TreeNode class. This code makes use
of the same properties of binary search trees that cause an inorder
traversal to print out the nodes in the tree from smallest to largest.
There are three cases to consider when looking for the successor:
If the node has a right child, then the successor is the smallest key in the right subtree.
If the node has no right child and is the left child of its parent, then the parent is the successor.
If the node is the right child of its parent, and itself has no right child, then the successor to this node is the successor of its parent, excluding this node.
The first condition is the only one that matters for us when deleting a
node from a binary search tree. However, the find_successor method
has other uses that we will explore in the exercises at the end of this
chapter.
The find_min method is called to find the minimum key in a subtree.
You should convince yourself that the minimum value key in any binary
search tree is the leftmost child of the tree. Therefore the find_min
method simply follows the left_child references in each node of the
subtree until it reaches a node that does not have a left child.
Listing 12
def find_successor(self):
successor = None
if self.right_child:
successor = self.right_child.find_min()
else:
if self.parent:
if self.is_left_child():
successor = self.parent
else:
self.parent.right_child = None
successor = self.parent.find_successor()
self.parent.right_child = self
return successor
def find_min(self):
current = self
while current.left_child:
current = current.left_child
return current
def splice_out(self):
if self.is_leaf():
if self.is_left_child():
self.parent.left_child = None
else:
self.parent.right_child = None
elif self.has_any_child():
if self.left_child:
if self.is_left_child():
self.parent.left_child = self.left_child
else:
self.parent.right_child = self.left_child
self.left_child.parent = self.parent
else:
if self.is_left_child():
self.parent.left_child = self.right_child
else:
self.parent.right_child = self.right_child
self.right_child.parent = self.parent
We can implement the del operator by
writing a __delete__ method for the
BinarySearchTree as shown in Listing 13.
It is a wrapper method that allows us to remove a key from the map
by writing del my_zip_tree["NYC"].
Listing 13
def __delitem__(self, key):
self.delete(key)
We need to look at one last interface method for the binary search tree.
Suppose that we would like to simply iterate over all the keys in the
tree in order. This is definitely something we have done with
dictionaries, so why not trees? You already know how to traverse a
binary tree in order, using the inorder traversal algorithm.
However, writing an iterator requires a bit more work since an iterator
should return only one node each time the iterator is called.
Python provides us with a very powerful function to use when creating an
iterator. The function is called yield. yield is similar to
return in that it returns a value to the caller. However, yield
also takes the additional step of freezing the state of the function so
that the next time the function is called it continues executing from
the exact point it left off earlier. Functions that create objects that
can be iterated are called generator functions.
The code for an inorder iterator of a binary tree is shown in the next
listing. Look at this code carefully; at first glance you
might think that the code is not recursive. However, remember that
__iter__ overrides the for ... in operation for iteration, so it
really is recursive! Because it is recursive over TreeNode instances,
the __iter__ method is defined in the TreeNode class.
def __iter__(self):
if self:
if self.left_child:
for elem in self.left_child:
yield elem
yield self.key
if self.right_child:
for elem in self.right_child:
yield elem
At this point you may want to download the entire file containing the
full version of the BinarySearchTree and TreeNode classes.