6.6. Nodes and References¶
Our second method to represent a tree uses nodes and references. In this case we will define a class that has attributes for the root value as well as the left and right subtrees. Using nodes and references, we might think of the tree as being structured like the one shown in Figure 2. Since this representation more closely follows the object-oriented programming paradigm, we will continue to use this representation for the remainder of the chapter.
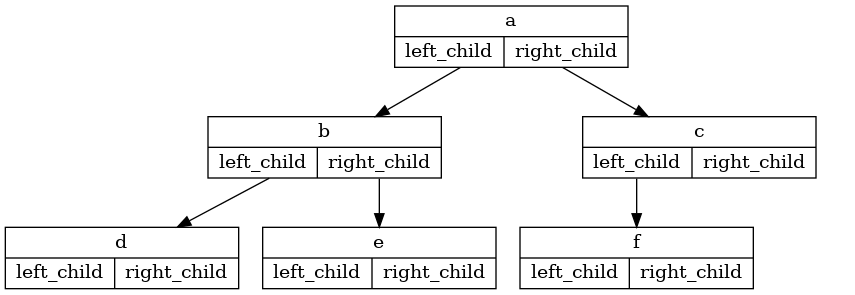
Figure 2: A Simple Tree Using a Nodes and References Approach¶
We will start out with a simple class definition for the nodes and
references approach as shown in Listing 4. The important thing
to remember about this representation is that the attributes left_child
and right_child will become references to other instances of the
BinaryTree class. For example, when we insert a new left child into
the tree, we create another instance of BinaryTree and modify
self.left_child in the root to reference the new tree.
Listing 4
class BinaryTree:
def __init__(self, root_obj):
self.key = root_obj
self.left_child = None
self.right_child = None
Notice that in Listing 4, the constructor function expects to
get some kind of object to store in the root. Just as you can store
any object you like in a list, the root object of a tree can be a
reference to any object. For our early examples, we will store the name
of the node as the root value. Using nodes and references to represent
the tree in Figure 2, we would create six instances of the
BinaryTree class.
Next let’s look at the functions we need to build the tree beyond the
root node. To add a left child to the tree, we will create a new binary
tree object and set the left_child attribute of the root to refer to this
new object. The code for insert_left is shown in
Listing 5.
Listing 5
1def insert_left(self, new_node):
2 if self.left_child is None:
3 self.left_child = BinaryTree(new_node)
4 else:
5 new_child = BinaryTree(new_node)
6 new_child.left_child = self.left_child
7 self.left_child = new_child
We must consider two cases for insertion. The first case is
characterized by a node with no existing left child. When there is no
left child, simply add a node to the tree. The second case is
characterized by a node with an existing left child. In the second
case, we insert a node and push the existing child down one level in the
tree. The second case is handled by the else statement on line
4 of Listing 5.
The code for insert_right must consider a symmetric set of cases.
There will either be no right child, or we must insert the node between
the root and an existing right child. The insertion code is shown in
Listing 6.
Listing 6
def insert_right(self, new_node):
if self.right_child == None:
self.right_child = BinaryTree(new_node)
else:
new_child = BinaryTree(new_node)
new_child.right_child = self.right_child
self.right_child = new_child
To round out the definition for a simple binary tree data structure, we will write accessor methods for the left and right children and for the root values (see Listing 7) .
Listing 7
def get_root_val(self):
return self.key
def set_root_val(self, new_obj):
self.key = new_obj
def get_left_child(self):
return self.left_child
def get_right_child(self):
return self.right_child
Now that we have all the pieces to create and manipulate a binary tree,
let’s use them to check on the structure a bit more. Let’s make a simple
tree with node a as the root, and add nodes “b” and “c” as children. ActiveCode 1 creates the tree and looks at the some of the
values stored in key, left_child, and right_child. Notice that both the
left and right children of the root are themselves distinct instances of
the BinaryTree class. As we said in our original recursive
definition for a tree, this allows us to treat any child of a binary
tree as a binary tree itself.
Self Check
Write a function build_tree that returns a tree using the nodes and references implementation that looks like this: