6.16. Balanced Binary Search Trees¶
In the previous section we looked at building a binary search tree. As
we learned, the performance of the binary search tree can degrade to
\(O(n)\) for operations like get and put when the tree
becomes unbalanced. In this section we will look at a special kind of
binary search tree that automatically makes sure that the tree remains
balanced at all times. This tree is called an AVL tree and is named
for its inventors: G.M. Adelson-Velskii and E.M. Landis.
An AVL tree implements the Map abstract data type just like a regular binary search tree; the only difference is in how the tree performs. To implement our AVL tree we need to keep track of a balance factor for each node in the tree. We do this by looking at the heights of the left and right subtrees for each node. More formally, we define the balance factor for a node as the difference between the height of the left subtree and the height of the right subtree.
Using the definition for balance factor given above, we say that a subtree is left-heavy if the balance factor is greater than zero. If the balance factor is less than zero, then the subtree is right-heavy. If the balance factor is zero, then the tree is perfectly in balance. For purposes of implementing an AVL tree and gaining the benefit of having a balanced tree, we will define a tree to be in balance if the balance factor is -1, 0, or 1. Once the balance factor of a node in a tree is outside this range we will need to have a procedure to bring the tree back into balance. Figure 1 shows an example of an unbalanced right-heavy tree and the balance factors of each node.
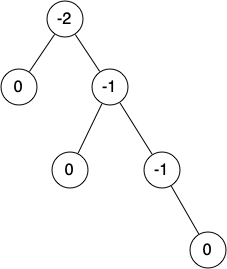
Figure 1: An Unbalanced Right-Heavy Tree with Balance Factors¶