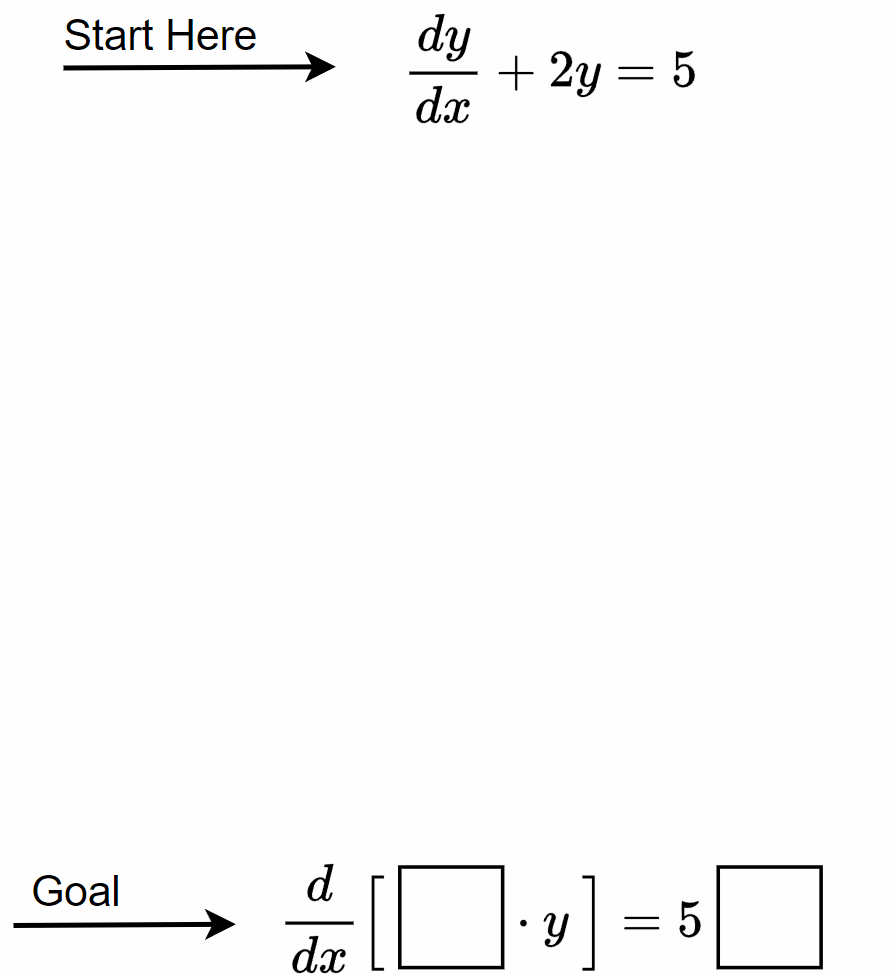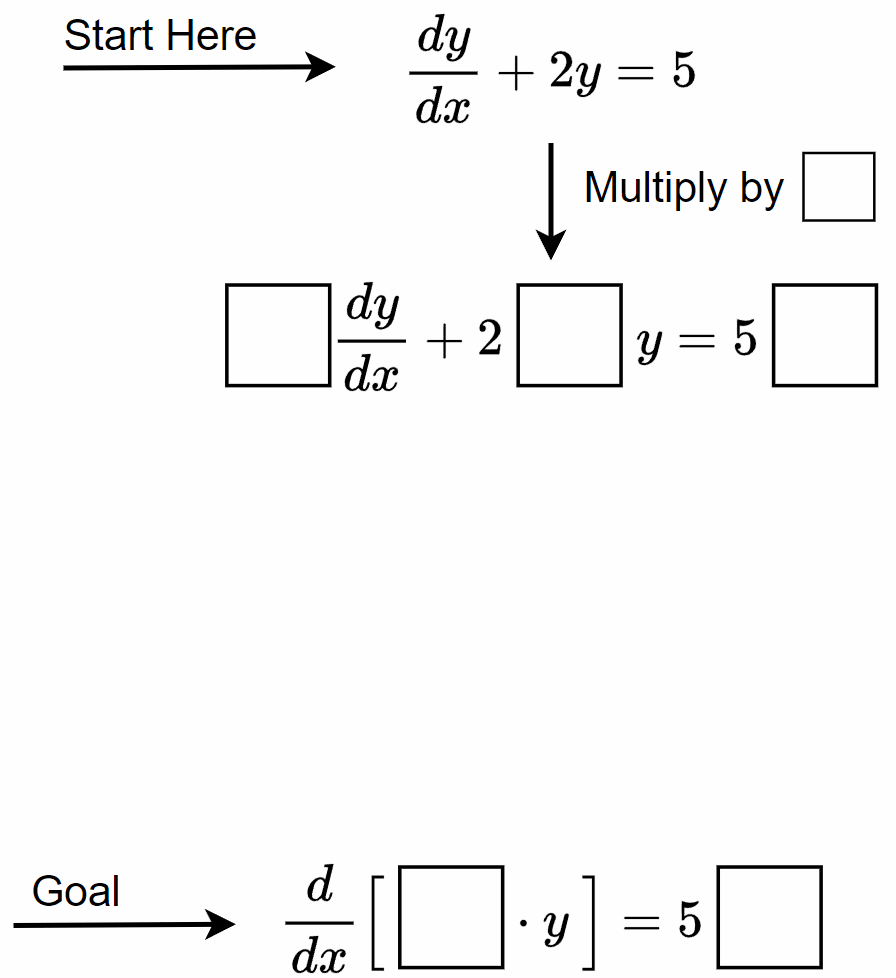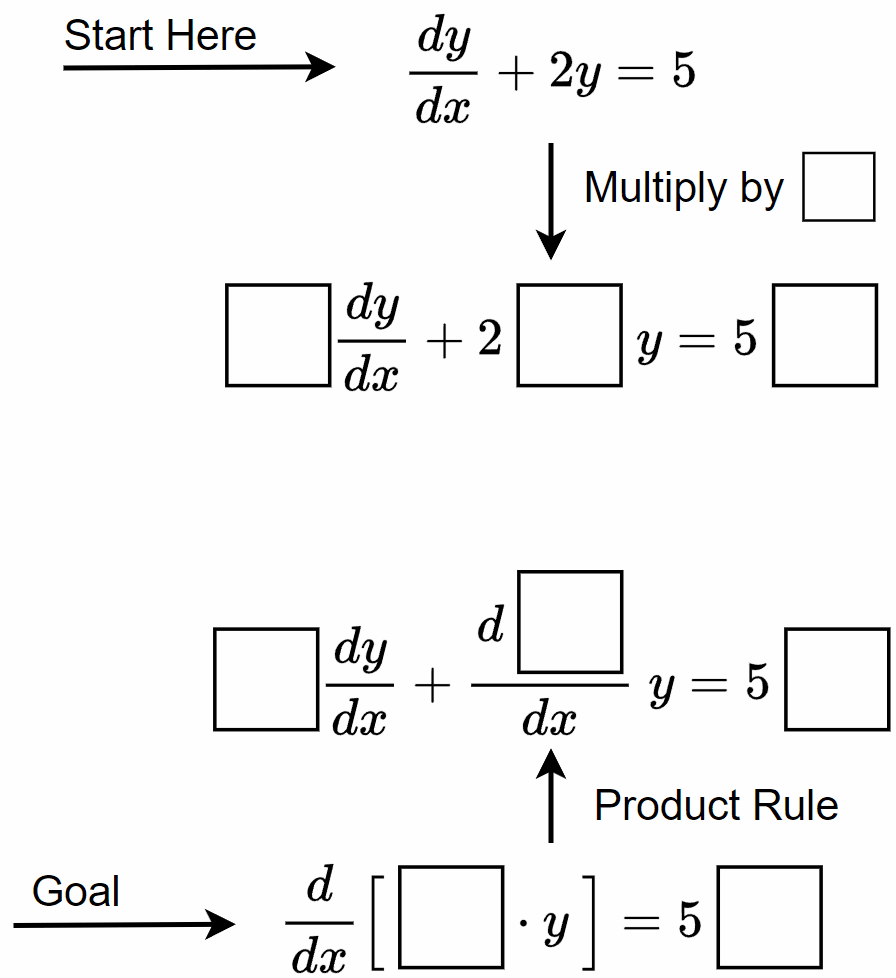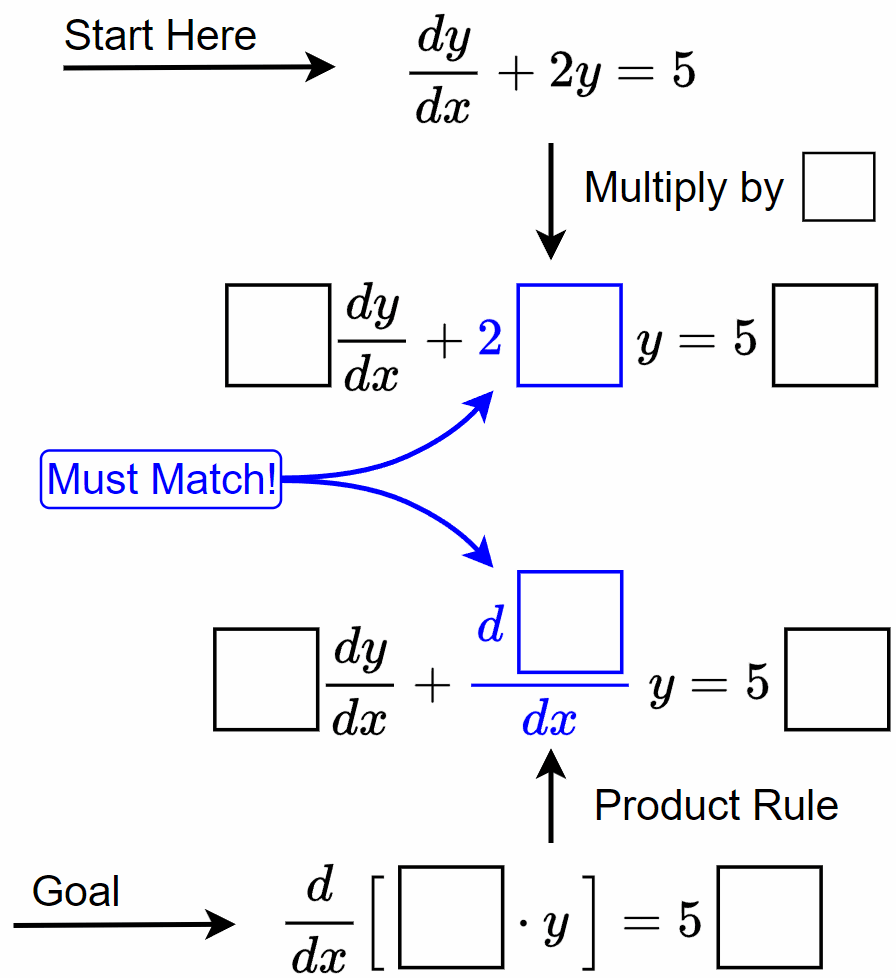Section 5.2 The Integrating Factor
In the previous section, we introduced the idea of solving first-order linear differential equations by manipulating the equation into a form that allows direct integration. This process involved applying a “backward” product rule to make the left-hand side a perfect derivative. However, most equations are not in the form to do this directly. Instead, there is a missing piece, called the integrating factor that is required for transformation to take place and is the focus of this section.
To see this “missing” piece, lets consider the differential equation:
\begin{equation}
\frac{dy}{dx} + 2y = 5 \text{.}\tag{8}
\end{equation}
We would like to apply the backward product rule to the left side, but it seems to be missing something. Let’s try to figure out what this missing piece is by multipying both sides by something:
\begin{equation}
\us{?}{\boxed{\phantom{\large |P}}}\frac{dy}{dx} + 2\ \us{?}{\boxed{\phantom{\large |P}}}\ y = 5\ \us{?}{\boxed{\phantom{\large |P}}}\text{.}\tag{9}
\end{equation}
With this missing piece and the fact that \(y\) and \(dy/dx\) appear in the equation, we should be able to rewrite the equation as:
\begin{equation}
\frac{d}{dx} \Big[\ \us{?}{\boxed{\phantom{\large |P}}} \cdot y\ \Big] = 5\ \us{?}{\boxed{\phantom{\large |P}}}\text{.}\tag{10}
\end{equation}
To determine what this missing piece is, we need to see where
(8) (start) and
(10) (goal) meet in the middle. This is shown below.
Notice, the two middle equations agree everywhere except for the expressions in blue. In order for the start and goal equations to be the same, these expressions must match. In other words, the piece that we need to get
(10) must satisfy
\begin{equation*}
{\color{blue} \frac{d\ \boxed{\phantom{|P}}}{dx} = 2\ \boxed{\phantom{|P}}} \text{.}
\end{equation*}
But, this is the differential equation
\begin{equation*}
\frac{d\mu}{dx} = 2 \mu
\end{equation*}
where \(\mu\) is the unknown!
Solving this requires you to notice that it is separable and a
quick calculation shows that
\(\mu = e^{2x}\) is the solution. Therefore, if you multiply both sides of
(8) by
\(\mu = e^{2x}\text{,}\) you can use the backward product rule to write the equation as
\begin{equation*}
\frac{d}{dx}\left[ e^{2x} \cdot y \right] = 5e^{2x} \text{,}
\end{equation*}
The function, \(\mu = e^{2x}\text{,}\) that allowed us to rewrite the equation is called the integrating factor and it is derived by solving a simple separable equation based on the coefficient of the dependent variable in the differential equation. Once the integrating factor is found, it allows us to rewrite the equation into a form that is straightforward to solve.
Concept 46. The Integrating Factor.
The integrating factor for the first-order linear differential equation
\begin{equation*}
y' + P(x)y = Q(x)
\end{equation*}
is \(\mu = e^{\int P(x) dx}\text{.}\) Multiplying both sides by \(\mu\) transforms the equation into:
\begin{equation*}
\frac{d}{dx}\left[\mu(x) \cdot y\right] = \mu(x)Q(x)\text{.}
\end{equation*}
Derivation of the Integrating Factor.
Note, all first-order linear differential equations can be written in the form
\begin{equation}
\frac{dy}{dx} + P(x) y = Q(x)\text{,}\tag{11}
\end{equation}
where
\(P(x)\) and
\(Q(x)\) are functions of
\(x\text{.}\) The goal is to write the left-side as a single derivative. However, backward product rule is missing a piece,
\(\mu(x)\text{,}\) that we still need to find. We find
\(\mu(x)\) by multiplying it onto
(11), like so
\begin{align*}
\frac{dy}{dx} + P(x)\amp\ y = Q(x) \\
\mu \frac{dy}{dx} + {\color{blue} \mu P(} \amp\ {\color{blue}\! x)} y = \mu Q(x) \\
{\color{blue} \updownarrow}\ \ \amp \ {\color{blue} \text{match & solve}}\\
\mu \frac{dy}{dx} + {\color{blue} \frac{d\mu}{dx}}\amp\ y = \mu Q(x) \\
\frac{d}{dx}\big[\mu \cdot \amp\ y\big] = \mu Q(x)
\end{align*}
\begin{align*}
{\color{blue} \frac{d\mu}{dx} =}\amp\ {\color{blue} \mu P(x)} \\
{\color{blue} \frac{1}{\mu}d\mu =}\amp\ {\color{blue} P(x) dx} \\
{\color{blue} \int \frac{1}{\mu}d\mu =}\amp\ {\color{blue} \int P(x) dx} \\
{\color{blue} \ln|\mu| =}\amp\ {\color{blue} \int P(x) dx} \\
{\color{blue} \mu =}\amp\ {\color{blue} e^{\int P(x) dx}}
\end{align*}
Reading Questions Check your Understanding
1. What is the main purpose of an integrating factor?
What is the main purpose of an integrating factor in solving first-order linear differential equations?
- To transform the equation into one that can be solved using the backward product rule.
Correct! The integrating factor allows us to manipulate the equation so that it becomes a perfect derivative, which can then be integrated directly.
- To simplify the coefficients of the equation.
Not quite. While the integrating factor simplifies the process, its primary goal is to enable the use of the backward product rule, not to simplify the coefficients directly.
- To eliminate the constant term from the differential equation.
Incorrect. The integrating factor is used to transform the equation into a solvable form, not to remove constant terms.
- To reduce the equation to a second-order differential equation.
Incorrect. The integrating factor helps solve first-order differential equations, not reduce them to second-order equations.
2. Which of the following is the differential equation for the integrating factor \(\mu\text{?}\)
Which differential equation do you solve to find the integrating factor,\(\mu\text{,}\) for the first-order linear equation
\begin{equation*}
y' + \frac{y}{x} = \sin x\text{?}
\end{equation*}
- \(\mu' = \sin x\mu \)
Incorrect. Try again.
- \(\mu' = \frac{1}{x}\mu \)
Correct!
- \(\mu' + \frac{\mu}{x} = \sin x \)
Incorrect. Try again.
- \(\mu' = \frac{y}{x}\mu \)
Incorrect. Try again.
3. What form does the first-order linear differential equation take after multiplying by the integrating factor?
After multiplying both sides of a first-order linear differential equation by the integrating factor, the equation takes the form:
- \(\ds\frac{d}{dx}\left[\mu \cdot y\right] = \mu Q(x)\)
Correct! Multiplying by the integrating factor transforms the equation into this form.
- \(\ds\frac{d}{dx} \left[ y \right] = P(x) \mu Q(x)\)
Incorrect. The correct form is \(\frac{d}{dx}\left[\mu(x) \cdot y\right] = \mu(x)Q(x)\text{.}\)
- \(\ds\frac{d}{dx} \left[ y \right] + P(x)y = Q(x)\)
Incorrect. This is the form of the original equation before multiplying by the integrating factor.
- \(\ds\mu \cdot y = Q(x) \cdot \frac{dy}{dx}\)
Incorrect. This form does not represent the transformed equation after multiplying by the integrating factor.
4. What is the integrating factor for the equation \(y' + 3y = e^x\text{?}\)
Find the integrating factor for the equation \(y' + 3y = e^x\text{.}\)
- \(\ds\mu = e^{e^{3x}}\)
Incorrect. This is not the correct expression for the integrating factor.
- \(\mu = e^{3x}\)
Correct! The integrating factor is \(e^{3x}\text{.}\)
- \(\ds\mu = e^{x^2/2}\)
Incorrect. The correct integrating factor should involve the integral of the coefficient of \(y\text{,}\) which is \(3\text{,}\) not \(x\text{.}\)
- \(\ds\mu = e^{x}\)
Incorrect. This is not the correct form for the integrating factor.
5. If we solve a differential equation to find the integrating factor, then why doesn’t it contain an integration constant?
When solving a differential equation to find the integrating factor, why is there no constant of integration in the solution?
Since any value of this constant would give a valid integrating factor, we set the constant to the simplest value.
Correct! The integrating factor is used to multiply both sides of the equation, and any constant would cancel out during this process, making the constant irrelevant.
Because the integrating factor must be a specific function with no additional constants.
Incorrect. The integrating factor is determined by the form of the differential equation, but the lack of a constant is not because it must be a specific function—it’s because any constant would cancel out when multiplying both sides.
Because the integrating factor equation doesn’t have an initial condition.
Incorrect. Although the integrating factor equation doesn’t have an initial condition, this is not the reason it does not have one.
Because the constant of integration is already included in the solution for \(y\text{.}\)
Incorrect. The constant of integration appears in the final solution for \(y\text{,}\) but it is not related to why the integrating factor does not include a constant.
You have attempted
of
activities on this page.