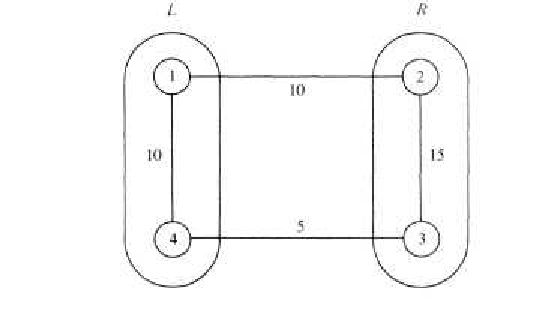
Suppose that no minimal spanning tree including \(e^*\) exists. Let \(T = (V, E')\) be a minimal spanning tree. If we add \(e^*\) to \(T\text{,}\) a cycle is created, and this cycle must contain another bridge, \(e\text{,}\) between \(L\) and \(R\text{.}\) Since \(w\left(e^*\right) \leq w(e)\text{,}\) we can delete \(e\) and the new tree, which includes \(e^*\) must also be a minimal spanning tree.