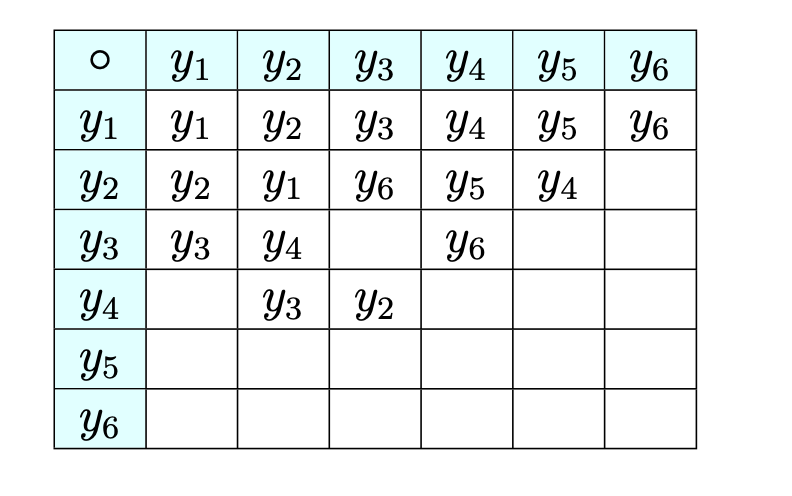
The terms “generic” and “trade” for prescription drugs are analogous to “generic” and “concrete” algebraic systems. Generic aspirin, for example, has no name, whereas Bayer, Tylenol, Bufferin, and Anacin are all trade or specific types of aspirins. The same can be said of a generic group \([G; *]\) where \(G\) is a nonempty set and \(*\) is a binary operation on \(G\text{,}\) When examples of typical domain elements can be given along with descriptions of how operations act on them, such as \(\mathbb{Q}\)* or \(M_{2\times 2}(\mathbb{R})\text{,}\) then the system is concrete (has a specific name, as with the aspirin). Generic is a way to describe a general algebraic system, whereas a concrete system has a name or symbols making it distinguishable from other systems.