Time estimate: 90 min.

7.5. Searching Algorithms¶

Computers store vast amounts of data. One of the strengths of computers is their ability to find things quickly. This ability is called searching. For the AP CSA exam you will need to know both linear (sequential) search and binary search algorithms.

The following video is also on YouTube at https://youtu.be/DHLCXXX1OtE. It introduces the concept of searching including sequential search and binary search.

Sequential or Linear search typically starts at the first element in an array or ArrayList and looks through all the items one by one until it either finds the desired value and then it returns the index it found the value at or if it searches the entire array or list without finding the value it returns -1.
Binary search can only be used on data that has been sorted or stored in order. It checks the middle of the data to see if that middle value is less than, equal, or greater than the desired value and then based on the results of that it narrows the search. It cuts the search space in half each time.

If binary search requires the values in an array or list to be sorted, how can you do that? There are many sorting algorithms which are covered in the next lesson.

7.5.1. Sequential Search¶

Sequential or linear search can be used to find a value in unsorted data. It usually starts at the first element and walks through the array or list until it finds the value it is looking for and returns its index. If it reaches the end of the array or list without finding the value, the search method usually returns a -1 to show that it didn’t find the value in the array or list. Click on Show CodeLens below to see linear search in action.

The code for sequentialSearch for arrays below is from a previous AP CSA course description. Click on the Code Lens button to see this code running in the Java visualizer.

public class ArraySearcher
{

/**
     * Finds the index of a value in an array of integers.
     *
     * @param elements an array containing the items to be searched.
     * @param target the item to be found in elements.
     * @return an index of target in elements if found; -1 otherwise.
     */
    public static int sequentialSearch(int[] elements, int target)
    {
        for (int j = 0; j < elements.length; j++)
        {
            if (elements[j] == target)
            {
                return j;
            }
        }
        return -1;
    }

public static void main(String[] args)
    {
        int[] numArray = {3, -2, 9, 38, -23};
        System.out.println("Tests of sequentialSearch");
        System.out.println(sequentialSearch(numArray, 3));
        System.out.println(sequentialSearch(numArray, 9));
        System.out.println(sequentialSearch(numArray, -23));
        System.out.println(sequentialSearch(numArray, 99));
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

public class RunestoneTests extends CodeTestHelper
{
    @Test
    public void testMain() throws IOException
    {
        String output = getMethodOutput("main");
        String expect = "Tests of sequentialSearch\n0\n2\n4\n-1";
        boolean passed = getResults(expect, output, "Expected output from main", true);
        assertTrue(passed);
    }
}

Here is the same search with an ArrayList. The same algorithms can be used with arrays or ArrayLists, but notice that size() and get(i) are used with ArrayLists instead of length and [i] which are used in arrays. Many of our examples will use arrays for simplicity since with arrays, we know how many items we have and the size won’t change during runtime. There are methods such as contains that can be used in ArrayLists instead of writing your own algorithms. However, they are not in the AP CSA Java subset.

Here is a linear search using ArrayLists. Notice that size() and get(i) is used with ArrayLists instead of length and [i] which are used in arrays. Click on the Code Lens button to step through this code in the visualizer.

import java.util.*;

public class ArrayListSearcher
{

/**
     * Finds the index of a value in an ArrayList of integers.
     *
     * @param elements an array containing the items to be searched.
     * @param target the item to be found in elements.
     * @return an index of target in elements if found; -1 otherwise.
     */
    public static int sequentialSearch(ArrayList<Integer> elements, int target)
    {
        for (int j = 0; j < elements.size(); j++)
        {
            if (elements.get(j) == target)
            {
                return j;
            }
        }
        return -1;
    }

public static void main(String[] args)
    {
        ArrayList<Integer> numList = new ArrayList<Integer>();
        numList.add(3);
        numList.add(-2);
        numList.add(9);
        numList.add(38);
        numList.add(-23);
        System.out.println("Tests of sequentialSearch");
        System.out.println(sequentialSearch(numList, 3));
        System.out.println(sequentialSearch(numList, 9));
        System.out.println(sequentialSearch(numList, -23));
        System.out.println(sequentialSearch(numList, 99));
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

Check Your Understanding

7-5-4: Which will cause the longest execution of a sequential search looking for a value in an array of integers?

The value is the first one in the array
This would be true for the shortest execution. This would only take one execution of the loop.
The value is in the middle of the array
Why would this be the longest execution?
The value is the last one in the array
There is one case that will take longer.
The value isn't in the array
A sequential search loops through the elements of an array or list starting with the first and ending with the last and returns from the loop as soon as it finds the passed value. It has to check every value in the array when the value it is looking for is not in the array.

7-5-5: Which will cause the shortest execution of a sequential search looking for a value in an array of integers?

The value is the first one in the array
This would only take one execution of the loop.
The value is in the middle of the array
Are you thinking of binary search?
The value is the last one in the array
This would be true if you were starting at the last element, but the algorithm in the course description starts with the first element.
The value isn't in the array
This is true for the longest execution time, but we are looking for the shortest.

You can also look for a String in an array or list, but be sure to use equals rather than ==. Remember that == is only true when the two references refer to the same String object, while equals returns true if the characters in the two String objects are the same.

Demonstration of a linear search for a String. Click on the Code Lens button or the link below to step through this code.

public class SearchTest
{

public static int sequentialSearch(String[] elements, String target)
    {
        for (int j = 0; j < elements.length; j++)
        {
            if (elements[j].equals(target))
            {
                return j;
            }
        }
        return -1;
    }

public static void main(String[] args)
    {
        String[] arr1 = {"blue", "red", "purple", "green"};

// test when the target is in the array
        int index = sequentialSearch(arr1, "red");
        System.out.println(index);

// test when the target is not in the array
        index = sequentialSearch(arr1, "pink");
        System.out.println(index);
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

public class RunestoneTests extends CodeTestHelper
{
    @Test
    public void testMain() throws IOException
    {
        String output = getMethodOutput("main");
        String expect = "1\n-1";
        boolean passed = getResults(expect, output, "Expected output from main", true);
        assertTrue(passed);
    }
}

7.5.2. Binary Search¶

How do you search for something in a phone book or dictionary that is in alphabetical or numerical order? If you’re looking for something beginning with M or on page 100 in a 200 page book, you wouldn’t want to start with page 1. You would probably start looking somewhere in the middle of the book. This is the idea behind binary search.

If your array or list is already in order (sorted), binary search will on average find an element or determine that it is missing much more quickly than a linear search. But binary search can only be used if the data is sorted.

Binary search keeps dividing the sorted search space into half. It compares a target value to the value in the middle of a range of indices. If the value isn’t found it looks again in either the left or right half of the current range. Each time through the loop it eliminates half the values in the search area until either the value is found or there is no more data to look at. See the animation below from https://github.com/AlvaroIsrael/binary-search:

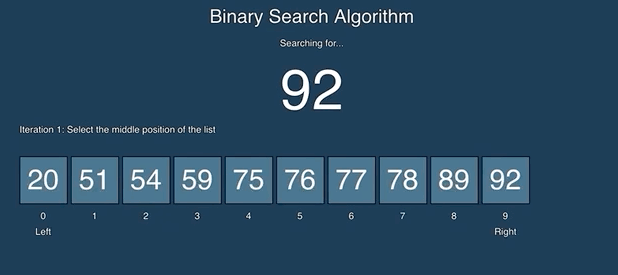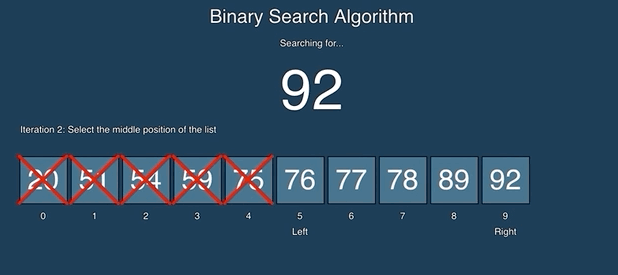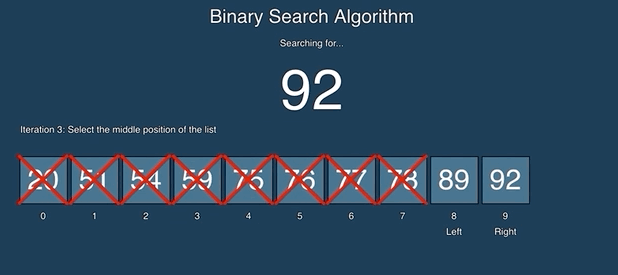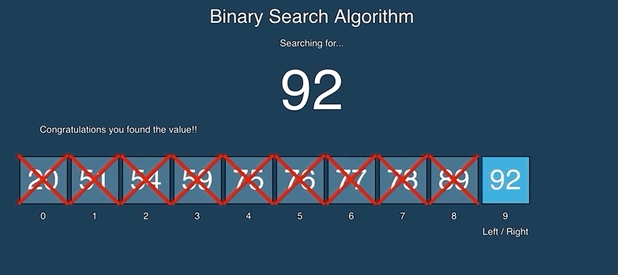
Binary search calculates the middle index as left + right / 2 where left starts out at 0 and right starts out at the array length - 1 (the index of the last element). Remember that integer division gives an integer result so 2.5 becomes 2. It compares the value at the middle index with the target value (the value you are searching for). If the target value is less than the value at the middle it sets right to middle minus one. If the target value is greater than the value at the middle it sets left to middle plus one. Otherwise the values match and it returns the middle index. It also stops when left is greater than right which indicates that the value wasn’t found and it returns -1.

The code for binarySearch below is from the AP CSA course description. A recursive version of this algorithm will be covered in Unit 10.

Demonstration of iterative binary search. Click on the Code Lens button to step through this code.

public class SearchTest
{
    public static int binarySearch(int[] elements, int target)
    {
        int left = 0;
        int right = elements.length - 1;
        while (left <= right)
        {
            int middle = (left + right) / 2;
            if (target < elements[middle])
            {
                right = middle - 1;
            }
            else if (target > elements[middle])
            {
                left = middle + 1;
            }
            else
            {
                return middle;
            }
        }
        return -1;
    }

public static void main(String[] args)
    {
        int[] arr1 = {-20, 3, 15, 81, 432};

// test when the target is in the middle
        int index = binarySearch(arr1, 15);
        System.out.println(index);

// test when the target is the first item in the array
        index = binarySearch(arr1, -20);
        System.out.println(index);

// test when the target is in the array - last
        index = binarySearch(arr1, 432);
        System.out.println(index);

// test when the target is not in the array
        index = binarySearch(arr1, 53);
        System.out.println(index);
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

public class RunestoneTests extends CodeTestHelper
{
    @Test
    public void testMain() throws IOException
    {
        String output = getMethodOutput("main");
        String expect = "2\n0\n4\n-1";
        boolean passed = getResults(expect, output, "Expected output from main", true);
        assertTrue(passed);
    }
}

You can also use binary search with a String array. But, when you look for a String, be sure to use compareTo method rather than < or > which can only be used with primitive types. Remember how the String method compareTo works:

int compareTo(String other) returns a negative value if the current string is less than the other string, 0 if they have the same characters in the same order, and a positive value if the current string is greater than the other string.

Demonstration of binary search with strings using compareTo. Click on the Code Lens button to step through the code.

public class BinSearchStrings
{
    public static int binarySearch(String[] elements, String target)
    {
        int left = 0;
        int right = elements.length - 1;
        while (left <= right)
        {
            int middle = (left + right) / 2;
            if (target.compareTo(elements[middle]) < 0)
            {
                right = middle - 1;
            }
            else if (target.compareTo(elements[middle]) > 0)
            {
                left = middle + 1;
            }
            else
            {
                return middle;
            }
        }
        return -1;
    }

public static void main(String[] args)
    {
        String[] arr1 = {"apple", "banana", "cherry", "kiwi", "melon"};

// test when the target is in the middle
        int index = binarySearch(arr1, "cherry");
        System.out.println(index);

// test when the target is the first item in the array
        index = binarySearch(arr1, "apple");
        System.out.println(index);

// test when the target is in the array - last
        index = binarySearch(arr1, "melon");
        System.out.println(index);

// test when the target is not in the array
        index = binarySearch(arr1, "pear");
        System.out.println(index);
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

7.5.3. Runtimes¶

How do we choose between two algorithms that solve the same problem? They usually have different characteristics and runtimes which measures how fast they run. For the searching problem, it depends on your data.

Binary search is much faster than linear search, especially on large data sets, but it can only be used on sorted data. Often with runtimes, computer scientist think about the worst case behavior. With searching, the worst case is usually if you cannot find the item. With linear search, you would have to go through the whole array before realizing that it is not there, but binary search is much faster even in this case because it eliminates half the data set in each step. We can measure an informal runtime by just counting the number of steps.

Here is a table that compares the worst case runtime of each search algorithm given an array of n elements. The runtime here is measured as the number of times the loop runs in each algorithm or the number of elements we need to check in the worst case when we don’t find the item we are looking for. Notice that with linear search, the worst case runtime is the size of the array n, because it has to look through the whole array. For the binary search runtime, we can calculate the number of times you can divide n in half until you get to 1. So, for example 8 elements can be divided in half to narrow down to 4 elements, which can be further divided in half to narrow down to 2 elements, which can be further divided in half to get down to 1 element, and then if that is wrong, to 0 elements, so that is 4 divisions or guesses to get the answer (8->4->2->1->0). In the table below, every time we double the size of N, we need at most one more guess or comparison with binary search. It’s much faster than linear search!

N	Linear Search	Binary Search
2	2 comparisons	2 comparisons
4	4	3
8	8	4
16	16	5
100	100	7

Runtimes can be described with mathematical functions. For an array of size n, linear search runtime is a linear function, and binary search runtime is a function of log base 2 of n (or log n + 1 comparisons). This is called the big-O runtime function in computer science, for example O(log n) vs. O(n). You can compare the growth of functions like n and log₂n as n, the data size, grows and see that binary search runs much faster for any n. You don’t need to know the log n runtime growth function for the AP exam, but you should be able to calculate how many steps binary search takes for a given n by counting how many times you can divide it in half. Or you can start at 1 and keep a count of how many times you can double it with the powers of two (1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, etc.) until you reach a number that is slightly above n.

Check Your Understanding

7-5-9: Which will cause the shortest execution of a binary search looking for a value in an array of integers?

The value is the first one in the array
This would be true for sequential search, not binary.
The value is in the middle of the array
If the value is in the middle of the array the binary search will return after one iteration of the loop.
The value is the last one in the array
How would that be the shortest in a binary search?
The value isn't in the array
This is true for the longest execution time, but we are looking for the shortest.

7-5-10: Which of the following conditions must be true in order to search for a value using binary search?

I. The values in the array must be integers.
II. The values in the array must be in sorted order.
III. The array must not contain duplicate values.

I only
You can use a binary search on any type of data that can be compared, but the data must be in order.
I and II
You can use a binary search on any type of data that can be compared.
II only
The only requirement for using a Binary Search is that the values must be ordered.
II and III
The array can contain duplicate values.

7-5-11: How many times would the loop in the binary search run for an array int[] arr = {2, 10, 23, 31, 55, 86} with binarySearch(arr,55)?

2
It will first compare with the value at index 2 and then index 4 and then return 4.
1
This would be true if we were looking for 23.
3
This would be true if we were looking for 31.

7-5-12: If you had an ordered array of size 500, what is the maximum number of iterations required to find an element with binary search?

approximately 15 times
How many times can you divide 500 in half?
approximately 9 times
You can divide 500 in half, 9 times, or you can observe that 2^9 = 512 which is slightly bigger than 500.
500 times
How many times can you divide 500 in half?
2 times
How many times can you divide 500 in half?

7.5.4. Programming Challenge : Search Runtimes¶

Let’s go back to the spellchecker that we created in Unit 6. Here is a version of the spellchecker below that reads the dictionary file into an ArrayList. The advantage of using an ArrayList instead of an array for the dictionary is that we do not need to know or declare the size of the dictionary in advance.

In Unit 6, we used linear search to find a word in the dictionary. However, the dictionary file is actually in alphabetical order. We could have used a much faster binary search algorithm! Let’s see how much faster we can make it.

Write a linear search method and a binary search method to search for a given word in the dictionary using the code in this lesson as a guide. You will need to use size and get(i) instead of [] to get an element in the ArrayList dictionary at index i. You will need to use the equals and compareTo methods to compare Strings. Have the methods return a count of how many words they had to check before finding the word or returning.

This spellchecker uses an ArrayList for the dictionary. Write a linearSearch(word) and a binarySearch(word) method. Use get(i), size(), equals, and compareTo. Return a count of the number of words checked.

import java.io.*;
import java.nio.file.*;
import java.util.*;

public class SpellChecker
{
    private ArrayList<String> dictionary;

/* Constructor populates the dictionary ArrayList from the file dictionary.txt*/
    public SpellChecker() throws IOException
    {
        List<String> lines = Files.readAllLines(Paths.get("dictionary.txt"));
        dictionary = new ArrayList<String>(lines);
    }

/**
     * Write a linearSearch(word) method that finds a word
     * in the ArrayList dictionary. It should also keep
     * a count of the number of words checked.
     *
     * @param String word to be found in elements.
     * @return a count of how many words checked before returning.
     */
    public int linearSearch(String word)
    {

}

/**
     * Write a binarySearch(word) method that finds the word
     * in the ArrayList dictionary. It should also keep
     * a count of the number of words checked.
     *
     * @param String word to be found in elements.
     * @return a count of how many words checked before returning.
     */
    public int binarySearch(String word)
    {

}

public static void main(String[] args) throws IOException
    {
        SpellChecker checker = new SpellChecker();
        String word = "catz";
        int i = checker.linearSearch(word);
        System.out.println("Linear search steps for " + word + " = " + i);
        int count = checker.binarySearch(word);
        System.out.println("Binary search steps for " + word + " = " + count);
    }
}

====
import static org.junit.Assert.*;
import org.junit.*;
import java.io.*;

public class RunestoneTests extends CodeTestHelper
{
    public RunestoneTests()
    {
       super("SpellChecker");
    }

@Test
   public void test1()
   {
       Object[] args = {"medium"};
       String output = getMethodOutput("linearSearch", args);
       String expect = "5549";

boolean passed =
               getResults(
                       expect,
                       output,
                       "linearSearch(\"medium\")"
                       );
       assertTrue(passed);
   }

@Test
   public void test2()
   {
       Object[] args = {"medium"};
       String output = getMethodOutput("binarySearch", args);
       String expect = "13";

boolean passed =
               getResults(
                       expect,
                       output,
                       "binarySearch(\"medium\")"
                       );
       assertTrue(passed);
   }
}

Run your code with the following test cases and record the runtime for each word in this Google document (do File/Make a Copy) also seen below to record your answers.

What do you notice? Which one was faster in general? Were there some cases where each was faster? How fast were they with misspelled words? Record your answers in the window below.

7-5-14: After you complete your code, write in your comparison of the linear vs. binary search runtimes based on your test cases. Were there any cases where one was faster than the other? How did each perform in the worst case when a word is misspelled?

7.5.5. Summary¶

There are standard algorithms for searching.
Sequential/linear search algorithms check each element in order until the desired value is found or all elements in the array or ArrayList have been checked.
The binary search algorithm starts at the middle of a sorted array or ArrayList and eliminates half of the array or ArrayList in each iteration until the desired value is found or all elements have been eliminated.
Data must be in sorted order to use the binary search algorithm. This algorithm will be covered more in Unit 10.
Informal run-time comparisons of program code segments can be made using statement execution counts.

You have attempted of activities on this page