7.13. Implementación de la gira del caballo¶
El algoritmo de búsqueda que usaremos para resolver el problema de la gira del caballo se denomina búsqueda en profundidad (BEP). Mientras que el algoritmo de búsqueda en anchura discutido en la sección anterior construye un árbol de búsqueda un nivel a la vez, una búsqueda en profundidad crea un árbol de búsqueda explorando una rama del árbol lo más profundamente posible. En esta sección veremos dos algoritmos que implementan una búsqueda en profundidad. El primer algoritmo que veremos resuelve directamente el problema de la gira del caballo al prohibir explícitamente que un nodo sea visitado más de una vez. La segunda implementación es más general, pero permite que los nodos sean visitados más de una vez a medida que se construye el árbol. La segunda versión se utiliza en las secciones subsiguientes para desarrollar algoritmos de grafos adicionales.
La exploración en profundidad del grafo es exactamente lo que necesitamos para encontrar una ruta que tiene exactamente 63 aristas. Veremos que cuando el algoritmo de búsqueda en profundidad encuentra un callejón sin salida (un lugar en el grafo donde no hay más movimientos posibles), él retrocede en el árbol al siguiente vértice más profundo que le permita realizar un movimiento legal.
La función giraCaballo recibe cuatro parámetros: n, la profundidad actual en el árbol de búsqueda; ruta, una lista de vértices visitados hasta el momento; u, el vértice en el grafo que deseamos explorar; y limite el número de nodos en la ruta. La función giraCaballo es recursiva. Cuando se llama a la función giraCaballo, ella verifica primero la condición del caso base. Si tenemos una ruta que contiene 64 vértices, regresamos de giraCaballo con un estado de True, indicando que hemos encontrado una gira exitosa. Si la ruta no es lo suficientemente larga, seguimos explorando un nivel más profundo eligiendo un nuevo vértice para explorar y llamando a giraCaballo recursivamente para ese vértice.
BEP también utiliza colores para realizar un seguimiento de qué vértices del grafo se han visitado. Los vértices no visitados son de color blanco, y los vértices visitados son de color gris. Habremos llegado a un callejón sin salida si todos los vecinos de un vértice particular han sido explorados y aún no hemos alcanzado nuestra longitud objetivo de 64 vértices. Cuando llegamos a un callejón sin salida debemos retroceder. El retroceso sucede cuando volvemos de giraCaballo con un estado de False. En la búsqueda en anchura utilizamos una cola para realizar un seguimiento de qué vértice se debe visitar a continuación. Dado que la búsqueda en profundidad es recursiva, estamos usando implícitamente una pila como ayuda para nuestro retroceso. Cuando volvemos de una llamada a giraCaballo con un estado de False, en la línea 11, permanecemos dentro del ciclo while y examinamos el siguiente vértice en listaVecinos.
Programa 3
from pythoned.grafos import Grafo, Vertice
def giraCaballo(n,ruta,u,limite):
u.asignarColor('gris')
ruta.append(u)
if n < limite:
listaVecinos = list(u.obtenerConexiones())
i = 0
hecho = False
while i < len(listaVecinos) and not hecho:
if listaVecinos[i].obtenerColor() == 'blanco':
hecho = giraCaballo(n+1, ruta, listaVecinos[i], limite)
i = i + 1
if not hecho: # prepararse para retroceder
ruta.pop()
u.asignarColor('blanco')
else:
hecho = True
return hecho
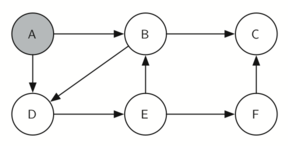
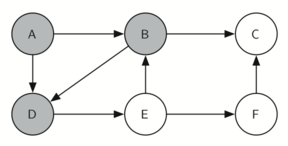
Veamos un ejemplo sencillo de giraCaballo en acción. Usted puede consultar las figuras que se muestran a continuación para seguir los pasos de la búsqueda. Para este ejemplo asumiremos que la llamada al método obtenerConexiones en la línea 6 ordena los nodos en orden alfabético. Comenzamos llamando a giraCaballo(0,ruta,A,6).
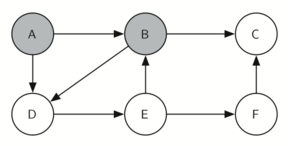
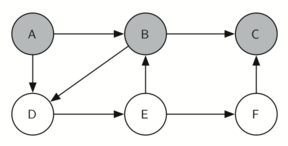
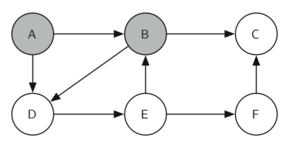
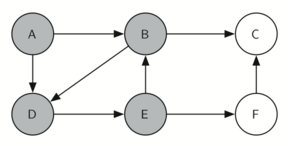
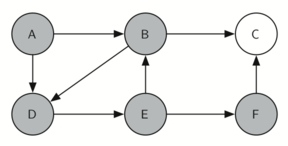
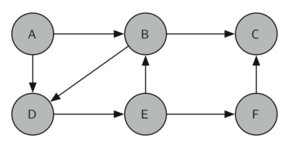
giraCaballo comienza con el nodo A (Figura 3). Los nodos adyacentes a A son B y D. Como B está alfabéticamente antes de D, BEP selecciona a B para la expansión subsiguiente como se muestra en la Figura 4. La exploración de B ocurre cuando giraCaballo es llamada recursivamente. B es adyacente a C y D, por lo que giraCaballo elige explorar C a continuación. Sin embargo, como se puede ver en la Figura 5, el nodo C es un callejón sin salida pues no tiene nodos blancos adyacentes. En este punto cambiamos el color del nodo C de nuevo a blanco. La llamada a giraCaballo devuelve un valor de False. El retorno de la llamada recursiva efectivamente retrocede la búsqueda al vértice B (ver la Figura 6). El siguiente vértice por explorar de la lista es el vértice D, por lo que giraCaballo hace una llamada recursiva moviéndose al nodo D (ver la Figura 7). Desde el vértice D, giraCaballo puede continuar haciendo llamadas recursivas hasta llegar nuevamente al nodo C (ver la Figura 8, la Figura 9 y la Figura 10). Sin embargo, esta vez, cuando llegamos al nodo C, la prueba n < limite falla, por lo que sabemos que hemos agotado todos los nodos del grafo. En este punto podemos devolver True para indicar que hemos hecho una gira exitosa del grafo. Cuando devolvemos la lista, ruta tiene los valores [A, B, D, E, F, C], que es el orden que necesitamos para recorrer el grafo y visitar cada nodo exactamente una vez.
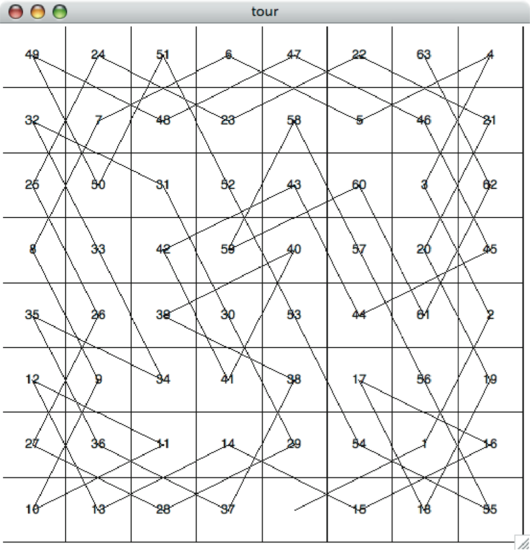
La Figura 11 muestra cómo luce una gira completa en un tablero de ocho por ocho. Hay muchas giras posibles; algunas son simétricas. Con algunas modificaciones se pueden hacer giras circulares que comienzan y terminan en el mismo cuadrado.