7.22. Algoritmo de Prim del árbol de expansión¶
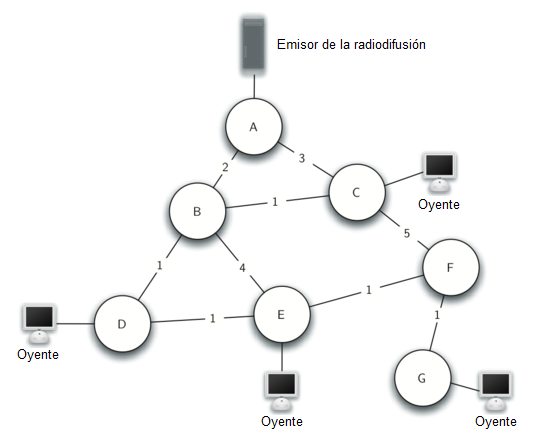
Para nuestro último algoritmo de grafos vamos a considerar un problema al que se enfrentan los diseñadores de juegos en línea y los proveedores de radio por Internet. El problema es que quieren transferir eficientemente una pieza de información a todos y cada uno de los que puedan estar escuchando. Esto es importante en los juegos para que todos los jugadores conozcan la posición más reciente de cada uno de los otros jugadores. Es importante también en la radio por Internet para que todos los oyentes que estén sintonizados estén recibiendo todos los datos que necesitan para reconstruir la canción que estén escuchando. La Figura 9 ilustra el problema de la radiodifusión.
Hay algunas soluciones de fuerza bruta a este problema, así que mirémoslas primero para ayudar a entender mejor el problema de la radiodifusión. Esto también le ayudará a apreciar la solución que vamos a proponer cuando hayamos terminado. Para comenzar, el emisor de la radiodifusión tiene cierta información que todos los oyentes necesitan recibir. La solución más simple es que el emisor de la radiodifusión mantenga una lista de todos los oyentes y envíe mensajes individuales a cada uno. En la Figura 9 mostramos una pequeña red con un radiodifusor y algunos oyentes. Utilizando este primer enfoque, se enviarían cuatro copias de cada mensaje. Suponiendo que se utilice la ruta de menor costo, veamos cuántas veces cada enrutador manejaría el mismo mensaje.
Todos los mensajes de la emisora pasan por el enrutador A, por lo que A ve las cuatro copias de cada mensaje. El enrutador C sólo ve una copia de cada mensaje para su oyente. Sin embargo, los enrutadores B y D verían tres copias de cada mensaje ya que los enrutadores B y D están en la ruta menos costosa para los oyentes 1, 2 y 3. Esto es un montón de tráfico extra si consideramos que el emisor de la radiodifusión debe enviar cientos de mensajes por segundo para una emisión de radio.
Una solución de fuerza bruta es que el emisor de la radiodifusión envíe una sola copia del mensaje de radiodifusión y deje que los enrutadores resuelvan las cosas. En este caso, la solución más sencilla es una estrategia llamada inundación no controlada. La estrategia de inundación funciona de la siguiente manera. Cada mensaje comienza con un valor de tiempo de vida (tdv) inicializado en un número mayor o igual al número de aristas entre el emisor de radiodifusión y su oyente más distante. Cada enrutador obtiene una copia del mensaje y pasa el mensaje a todos sus enrutadores vecinos. Cuando se transmite el mensaje, el tdv disminuye. Cada enrutador continúa enviando copias del mensaje a todos sus vecinos hasta que el valor tdv llegue a 0. Es fácil convencerse de que la inundación no controlada genera muchos más mensajes innecesarios que nuestra primera estrategia.
La solución a este problema radica en la construcción de un árbol de expansión de ponderación mínima. Formalmente definimos el árbol de expansión mínimo \(T\) para un grafo \(G = (V,E)\) como sigue. \(T\) es un subconjunto acíclico de \(E\) que conecta todos los vértices de \(V\). Se minimiza la suma de las ponderaciones de las aristas de \(T\).
En la Figura 10 se muestra una versión simplificada del grafo de radiodifusión, resaltando las aristas que forman un árbol de expansión mínimo para el grafo. Ahora para solucionar nuestro problema de radiodifusión, el emisor de la radiodifusión simplemente envía a la red una sola copia del mensaje de radiodifusión. Cada enrutador envía el mensaje a cualquier vecino que forme parte del árbol de expansión, excluyendo al vecino que acaba de enviarle el mensaje. En este ejemplo A reenvía el mensaje a B. B reenvía el mensaje a D y C. D reenvía el mensaje a E, el cual lo reenvía a F, y este último lo reenvía a G. Ningún enrutador ve más de una copia de cualquier mensaje, y todos los oyentes interesados ven una copia del mensaje.
Figura 10: Árbol de expansión mínimo para el grafo de difusión¶
Figura 10: Árbol de expansión mínimo para el grafo de difusión
El algoritmo que usaremos para resolver este problema se llama el algoritmo de Prim. El algoritmo de Prim pertenece a una familia de algoritmos llamados “algoritmos codiciosos” porque en cada paso elegiremos el siguiente paso más barato. En este caso, el siguiente paso más barato es seguir la arista que tenga la ponderación más baja. Nuestro último paso es desarrollar el algoritmo de Prim.
La idea básica en la construcción de un árbol de expansión es la siguiente:
Mientras que T no sea aún un árbol de expansión
Encontrar una arista que sea segura para agregarla al árbol
Agregar la nueva arista a T
El truco está en el paso que nos lleva a “encontrar una arista que sea segura”. Una arista segura se define como cualquier arista que conecta un vértice que está en el árbol de expansión con un vértice que no está en el árbol de expansión. Esto asegura que el árbol seguirá siendo siempre un árbol y que, por lo tanto, no tendrá ciclos.
El código en Python para implementar el algoritmo de Prim se muestra en el Programa 2. El algoritmo de Prim es similar al algoritmo de Dijkstra porque ambos usan una cola de prioridad para seleccionar el siguiente vértice que se agregará al grafo en crecimiento.
Programa 2
from pythoned.grafos import ColaPrioridad, Grafo, Vertice
def prim(G,inicio):
cp = ColaPrioridad()
for v in G:
v.asignarDistancia(sys.maxsize)
v.asignarPredecesor(None)
inicio.asignarDistancia(0)
cp.construirMonticulo([(v.obtenerDistancia(),v) for v in G])
while not cp.estaVacia():
verticeActual = cp.eliminarMin()
for verticeSiguiente in verticeActual.obtenerConexiones():
nuevoCosto = verticeActual.obtenerPonderacion(verticeSiguiente)
if verticeSiguiente in cp and nuevoCosto<verticeSiguiente.obtenerDistancia():
verticeSiguiente.asignarPredecesor(verticeActual)
verticeSiguiente.asignarDistancia(nuevoCosto)
cp.decrementarClave(verticeSiguiente,nuevoCosto)
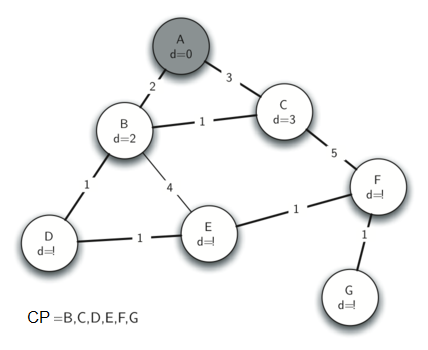
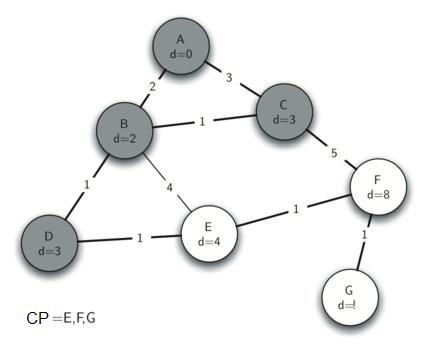
La siguiente secuencia de figuras (Figura 11 a Figura 17) muestra el algoritmo en funcionamiento sobre nuestro árbol de ejemplo. Comenzamos con A como vértice inicial. Las distancias a todos los otros vértices se inicializan en infinito. Observando a los vecinos de A podemos actualizar las distancias a dos de los vértices adicionales B y C porque las distancias a B y C, a través de A, son menores que infinito. Esto mueve a B y C al frente de la cola de prioridad. Actualizamos los enlaces a los predecesores para B y C haciendo que apunten a A. Es importante tener en cuenta que todavía no hemos añadido formalmente a B ni a C al árbol de expansión. Un nodo sólo se considera parte del árbol de expansión cuando es eliminado de la cola de prioridad.
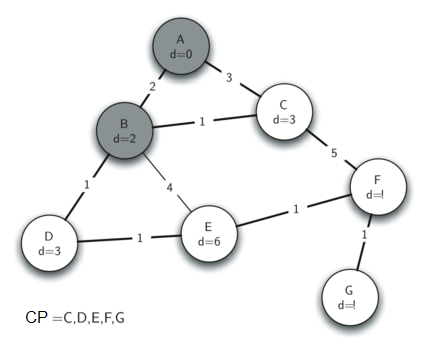
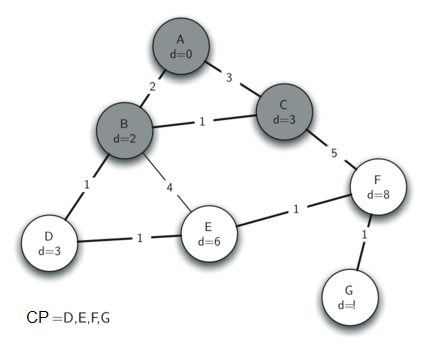
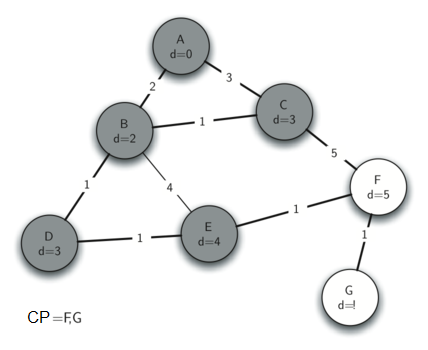
Puesto que B tiene la menor distancia, examinamos después a B. Examinando a los vecinos de B vemos que D y E pueden ser actualizados. Tanto D como E obtienen nuevos valores de distancia y se actualizan sus enlaces a los predecesores. Pasando al siguiente nodo en la cola de prioridad encontramos a C. El único nodo al que C es adyacente está todavía en la cola de prioridad, es F, por lo tanto podemos actualizar la distancia a F y ajustar la posición de F en la cola de prioridad.
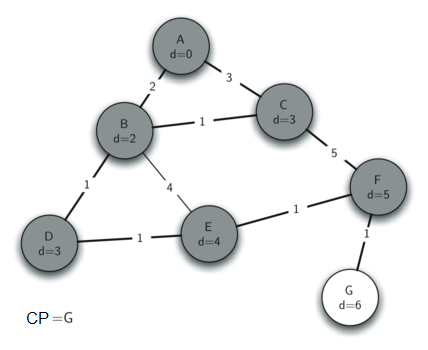
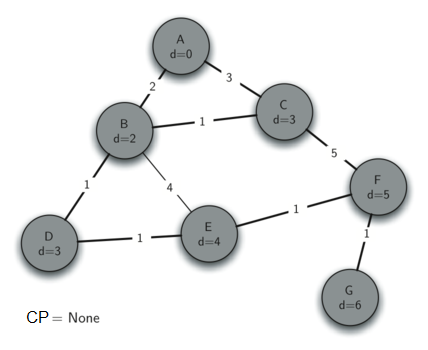
Ahora examinemos los vértices adyacentes al nodo D. Encontramos que podemos actualizar E y reducir la distancia a E de 6 a 4. Cuando hacemos esto cambiamos el enlace al predecesor en E para que apunte a D, preparándolo así para ser injertado en el árbol de expansión, pero en un lugar diferente. El resto del algoritmo continúa como se esperaría, agregando cada nuevo nodo al árbol.