7.9. Implementing Breadth-First Search¶
With the graph constructed we can now turn our attention to the algorithm we will use to find the shortest solution to the word ladder problem. The graph algorithm we are going to use is called the breadth-first search (BFS), and it is one of the easiest algorithms for searching a graph. It also serves as a prototype for several other important graph algorithms that we will study later.
Given a starting vertex \(s\) of a graph \(G\), a breadth first search proceeds by exploring edges in the graph to find all the vertices in \(G\) for which there is a path from \(s\). The remarkable thing about a breadth-first search is that it finds all the vertices that are a distance \(k\) from \(s\) before it finds any vertices that are a distance \(k+1\). One good way to visualize what the breadth-first search algorithm does is to imagine that it is building a tree, one level of the tree at a time. A breadth first search adds all children of the starting vertex before it begins to discover any of the grandchildren.
To keep track of its progress, BFS colors each of the vertices white, gray, or black. All the vertices are initialized to white when they are constructed. A white vertex is an undiscovered vertex. When a vertex is initially discovered it is colored gray, and when BFS has completely explored a vertex it is colored black. This means that once a vertex is colored black, it has no white vertices adjacent to it. A gray node, on the other hand, may have some white vertices adjacent to it, indicating that there are still additional vertices to explore.
The breadth-first search algorithm shown in Listing 2 below uses the
adjacency list graph representation we developed earlier. In addition it uses a Queue,
a crucial point as we will see, to decide which vertex to explore next.
Listing 2
from pythonds3.basic import Queue
from pythonds3.graphs import Graph
def bfs(start):
start.distance = 0
start.previous = None
vert_queue = Queue()
vert_queue.enqueue(start)
while vert_queue.size() > 0:
current = vert_queue.dequeue()
for neighbor in current.get_neighbors():
if neighbor.color == "white":
neighbor.color = "gray"
neighbor.distance = current.distance + 1
neighbor.previous = current
vert_queue.enqueue(neighbor)
current.color = "black"
The BFS algorithm uses an extended version of the Vertex
class that adds three new instance variables:
distance, previous, and color. Each of these instance variables also
has the appropriate getter and setter methods. The code for this
expanded Vertex class is included in the pythonds3 package, but we
will not show it to you here as there is nothing new to learn by seeing
the additional instance variables.
BFS begins at the starting vertex start and paints it gray to
show that it is currently being explored. Two other values, the distance
and the previous, are initialized to 0 and None respectively for
the starting vertex. Finally, start is placed on a Queue. The
next step is to begin to systematically explore vertices at the front of
the queue. We explore each new node at the front of the queue by
iterating over its adjacency list. As each node on the adjacency list is
examined, its color is checked. If it is white, the vertex is unexplored,
and four things happen:
The new unexplored vertex
neighboris colored gray.The predecessor of
neighboris set to the current nodecurrent.The distance to
neighboris set to the distance tocurrent + 1.neighboris added to the end of a queue. Addingneighborto the end of the queue effectively schedules this node for further exploration, but not until all the other vertices on the adjacency list ofcurrenthave been explored.
Let’s look at how the bfs function would construct the breadth-first
tree corresponding to the graph in Figure 1. Starting
from FOOL we take all nodes that are adjacent to FOOL and add them to
the tree. The adjacent nodes include POOL, FOIL, FOUL, and COOL. Each of
these nodes are added to the queue of new nodes to expand.
Figure 3 shows the state of the in-progress tree along with the
queue after this step.
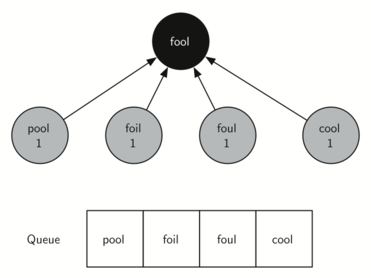
Figure 3: The First Step in the Breadth-First Search¶
In the next step bfs removes the next node (POOL) from the front of
the queue and repeats the process for all of its adjacent nodes.
However, when bfs examines the node COOL, it finds that the color of
COOL has already been changed to gray. This indicates that there is a
shorter path to COOL and that COOL is already on the queue for further
expansion. The only new node added to the queue while examining POOL is
POLL. The new state of the tree and queue is shown in Figure 4.
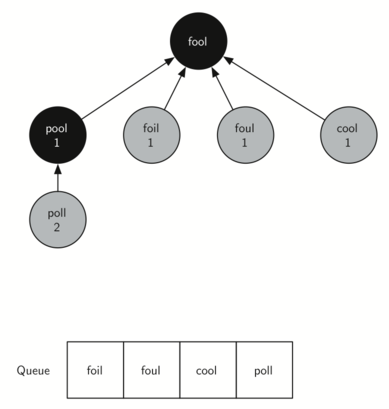
Figure 4: The Second Step in the Breadth-First Search¶
The next vertex on the queue is FOIL. The only new node that FOIL can
add to the tree is FAIL. As bfs continues to process the queue,
neither of the next two nodes adds anything new to the queue or the tree.
Figure 5 shows the tree and the queue after expanding all the
vertices on the second level of the tree.
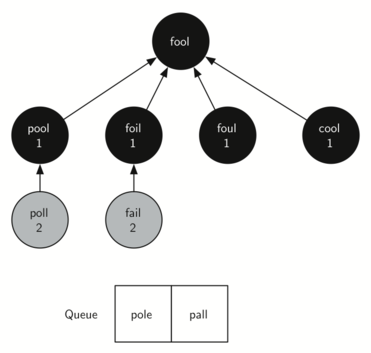
Figure 5: Breadth-First Search Tree After Completing One Level¶
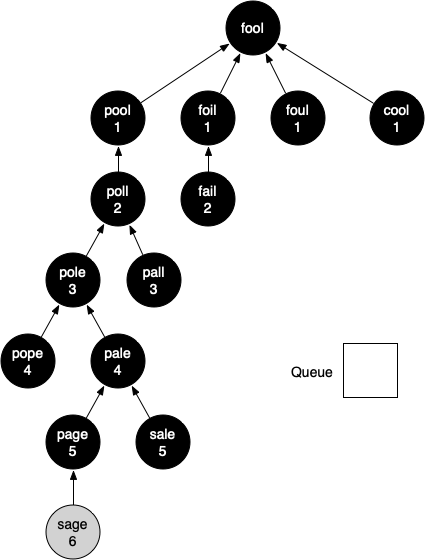
FIgure 6: Final Breadth-First Search Tree¶
You should continue to work through the algorithm on your own so that you are comfortable with how it works. Figure 6 shows the final breadth-first search tree after all the vertices in Figure 3 have been expanded. The amazing thing about the breadth-first search solution is that we have not only solved the FOOL–SAGE problem we started out with, but we have solved many other problems along the way. We can start at any vertex in the breadth-first search tree and follow the predecessor arrows back to the root to find the shortest word ladder from any word back to FOOL. The function below (Listing 3) shows how to follow the predecessor links to print out the word ladder.
Listing 3
def traverse(starting_vertex):
current = starting_vertex
while current:
print(current.key)
current = current.previous
traverse(g.get_vertex("sage"))