7.5. An Adjacency List¶
A more space-efficient way to implement a sparsely connected graph is to
use an adjacency list. In an adjacency list implementation, we keep a
master list of all the vertices in the Graph object, and each vertex
object in the graph maintains a list of the other vertices that it is
connected to. In our implementation of the Vertex class we will use
a dictionary rather than a list, where the dictionary keys are the
vertices and the values are the weights. Figure 4
illustrates the adjacency list representation for the graph in
Figure 2.
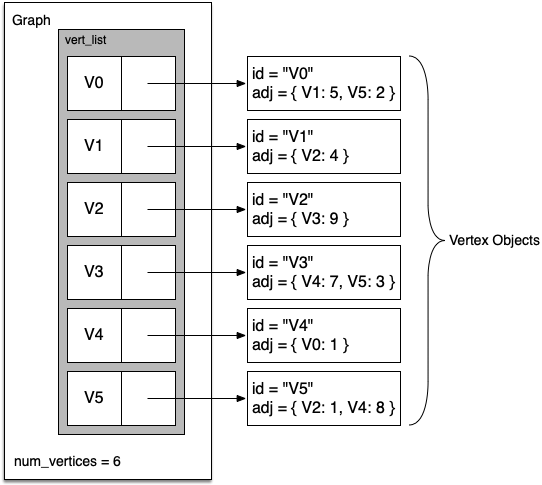
Figure 4: An Adjacency List Representation of a Graph¶
The advantage of the adjacency list implementation is that it allows us to compactly represent a sparse graph. The adjacency list also allows us to easily find all the links that are directly connected to a particular vertex.