
4.6. Coin Flip Experiment (optional)¶
Time Estimate: 45 minutes
4.6.1. Introduction and Goals¶
|
Coin Flip Experiment.
In this lesson you will use a slightly modified version of the app that you built in the preceding lesson, the Coin Flip Simulation tutorial.
The CoinFlipExperiment app will let you conduct an experiment aimed at determining how good App Inventor’s pseudorandom number generator (PRNG) is. The app will let you quickly "flip a coin" many times and display the results. In this lesson you will run the app several times, record and tally the results, and calculate the percentage of heads. The expectation is that as you flip a coin more times, the percentage of heads should approach 50%. |
|
|
Learning Objectives: I will learn to
Language Objectives: I will be able to
|
|
4.6.2. Learning Activities¶
Background
Here are some things you should know about how computers and computer languages (App Inventor) implement randomness:
- Randomness is used in lots of programs, especially games (Android Mash) and simulations (Coin Flip, 4-bit Computer Simulator).
- Creating a truly random process is hard to do. And creating a truly random process in a computer is no exception.
- Because creating true randomness is hard, computers use algorithms known as pseudo random number generators (PRNGs) to simulate randomness. This is much easier to do than generating truly random numbers. If you are curious about how PRNGs work, the next lesson goes into the details.
- PRNGs generate a sequence of "random seeming" numbers.
- PRNGs are models of true randomness. As such, they can be 'good' or 'bad' depending on how well they approximate true randomness. Much research by mathematicians and computer scientists goes into creating good PRNGs.
- App Inventor uses a standard and well established PRNG, which should do a good job of modeling randomness.
The Experiment
Our CoinFlip app simulates flipping a coin. If you had a fair coin and you flipped it many, many times -- maybe a million times -- then if it were truly fair, you would expect it to come up "Heads" half the time. That's why we say for any coin flip, it has a 50:50 chance of coming up heads.
App Inventor's random integer block uses its PRNG to
generate a random sequence of integers. In our app, the sequence is between 1
and 2 inclusive. So, if the PRNG is good, it should generate a 1 half the time and
a 2 half the time. And this, in turn, should let our Coin Flip app be a good model
of flipping a coin.
Hypothesis
Our hypothesis is that App Inventor’s random integer block is a good approximation of the process of randomly generating a 1 half the time and a 2 half the time.
If you were testing that a particular coin was “fair”, you would flip it lots of times and record the number of heads and tails. Their ratio should come out 50:50. But you have to do a lot of flips.
So, to test our hypothesis about App Inventor’s random integer block, we have to perform a simulated “coin flip” lots of times. To help with this, we will use the Coin Flip Experiment app, which will let us repeatedly “flip” a coin. The app uses an algorithm that uses the random integer block. If the random integer block is a good approximation of randomness, we would expect that when it is used to model the process of flipping a coin, it would make the odds of getting a “Heads” or “Tails” 50:50.
For our hypothesis to be true, the ratio between “Heads” and “Tails” in the app should approximate 50:50 as the number of trials gets large. The more trials we perform, the closer our ratio should be to 50:50.
If the ratio does approach 50:50, that would validate our hypothesis. If it does not, that would prove that our hypothesis is invalid.
Download and Install the App
If you have an Android mobile device, use the AI Companion app (or a barcode scanner app like ZXing Barcode Scanner) to scan this QR code to download and install the app directly to your mobile device. If you have an iOS device or are using the emulator, you will not be able to directly download and install an app, so download the source .aia file and import it into App Inventor and use the Connect/AI Companion to try it on your iOS device or Connect/Emulator. (Note: If you are having problems installing the app, you can use this Coin Toss Simulator website. If your Internet connection is not very good, you could also install the app ahead of time or at home so that it's available even without Internet.)
Reading the Source Code
Here is the source code for the app that is performing the experiment. As you can see, it is only slightly different from the version you created in the tutorial. The difference is an if statement after inputting N from the text box. The statement checks that N is a number (not the empty string) and that it’s no greater than 100,000.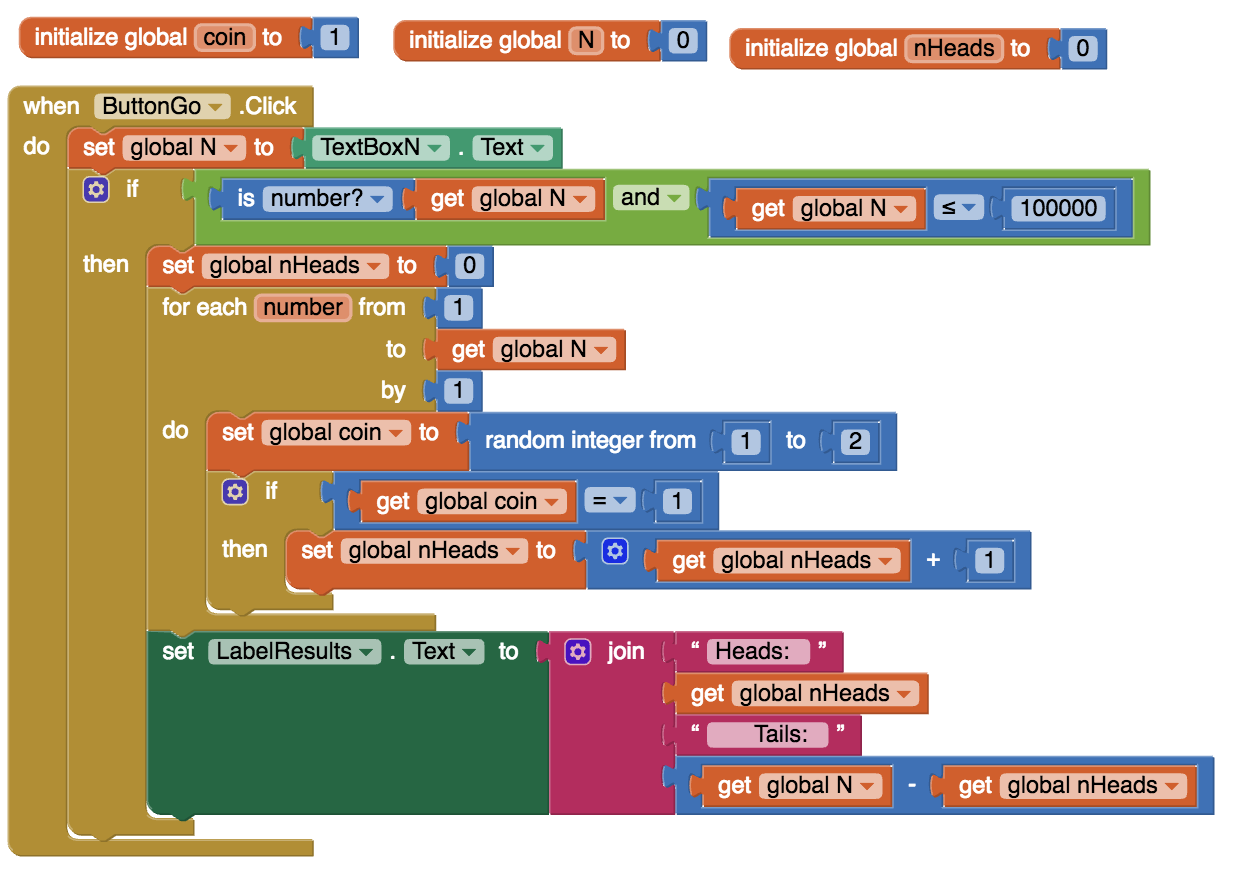
POGIL Activity for the Classroom (30 minutes)
Break into POGIL teams of 4. Each team member should download the coin flip app and run it on his or her device. Record your answers using this worksheet. (File-Make a Copy to have a version you can edit.) In addition, team members should take the following roles.| Role | Responsibility |
|---|---|
| Facilitator | Records the teams data -- i.e., the number of flips and the number of heads for each run of the app. Tallies the results and calculates the percentage of heads and tails. |
| Spokesperson | Reports the teams results. |
| Quality Control | Validates the Facilitator's data -- are the results of each run recorded correctly. Are the tallies and calculations correct? |
| Process Analyst | Keeps track of the teams progress and assesses its performance. |
Experimental Procedure
Our hypothesis for this experiment: App Inventor's PRNG provides a good model of randomness.
Perform the following steps.
- Repeatedly run the app on each device and record the number of heads and tails received in each trial. Do at least 20 runs (trials) among the team. The maximum number of "flips" per trial is 100. Your team should have at least 2000 "flips".
- Tally your results and calculate the percentage of heads for each trial. In addition, calculate the cumulative number and percentage of heads after each trial. For example, after the 5th trial of 100 flips, your table will show the number and percentage of heads for 500 flips.
- (Portfolio) Record your teams results for each trial in a neatly organized table. That is, if you did 20 trials
of 100 coin flips each, your table should have 20 rows of results, with the percentage for
each trial along with the cumulative numbers. Here's an example:
Here is a Google spreadsheet that you can use to record your data. Just enter your data in columns B and C. The rest of the columns will be calculated automatically.Trial Flips Heads % Heads Total Flips Total Heads Total % Heads 1 10000 4950 49.5 10000 4950 49.5% 2 10000 5040 50.4 20000 9990 49.95% - (Portfolio) According to your results, does App Inventor's PRNG provide a good model of randomness?
- (Portfolio) A friend claims that flipping a coin 100 times and finding that it comes up heads only 45% of the time shows that the coin is biased. How should you reply?
4.6.3. Summary¶
In this lesson, you learned how to:
4.6.4. Still Curious?¶
Hopefully this lesson has made you curious about how PRNGs work. If so, you should check out this lesson, which shows how to use some simple mathematics to create a PRNG.
4.6.5. Self-Check¶
Here is a table of the technical terms introduced in this lesson. Hover over the terms to review the definitions.
| model
PRNG fair coin hypothesis |
4.6.6. Reflection: For Your Portfolio¶
Answer the following portfolio reflection questions as directed by your instructor. Questions are also available in this Google Doc where you may use File/Make a Copy to make your own editable copy.