9.13. Improving our Pizza Price Predictions¶
In the last section, we made a simple model that allows us to predict the price of pizza based on its size. However, we know that there are many other factors, we will call them features, that go into the price of a pizza. In this section, we will investigate how we can improve our model by adding a feature corresponding to the number of toppings. The theory here is that with more information we should be able to do a better job of making predictions. Now, this little step makes the math a LOT more complicated, and it’s a lot harder to visualize what we are doing when we get past 3 dimensions! Fortunately, we can ignore the complicated math and let Solver do the heavy lifting. It turns out that it is not a big leap to go from one feature to several when using solver.
Our goal for solver is the same as it was before: we want to minimize the sum of squared errors. But we need to reframe the problem just slightly when we move past a single feature. Instead of finding the slope of a line, we need to find coefficients for each of our features. If you want to impress your friends and family, you could say that we are finding the coefficients that describe a hyperplane in n-dimensional space, where n is the number of features we have to work with. For the pizza problem, we might imagine that the kind of crust could be a third feature, and maybe the kind of sauce could be a fourth, etc. We will keep it simple for now and just add the number of toppings as that is all we need to do to see how we move from a single feature to any number of features. In addition to the number of toppings, we will need to calculate one more coefficient, which is akin to the y-intercept of the previous example. We will call this term the bias term, and it is necessary to include otherwise our hyperplane would always have to be centered at the origin - just like the best fit line would always go through the origin without the y-intercept.
If you want to think of it in terms of an equation, like the equation of a line, the equation would be \(w_1 v_1 + w_2 v_2 + w_3 v_3 + ... w_i v_i + w_b bias\). Most textbooks will simplify this equation by making the bias values \(w_0 v_0\) which will make the equation \(w_0 v_0 + w_2 v_2 + w_3 v_3 + ... w_i v_i\). The math:w_i terms are the coefficients that our algorithm (or Solver) will find for us, and the \(v_i\) terms are all of our observed values for the features.
To make this a bit easier to follow, we will rearrange our spreadsheet a bit as shown in the screenshot below. The area with the green background is for the coefficients for our features. We will let Solver figure out what values should go in there in order to minimize the MSE with the yellow background.
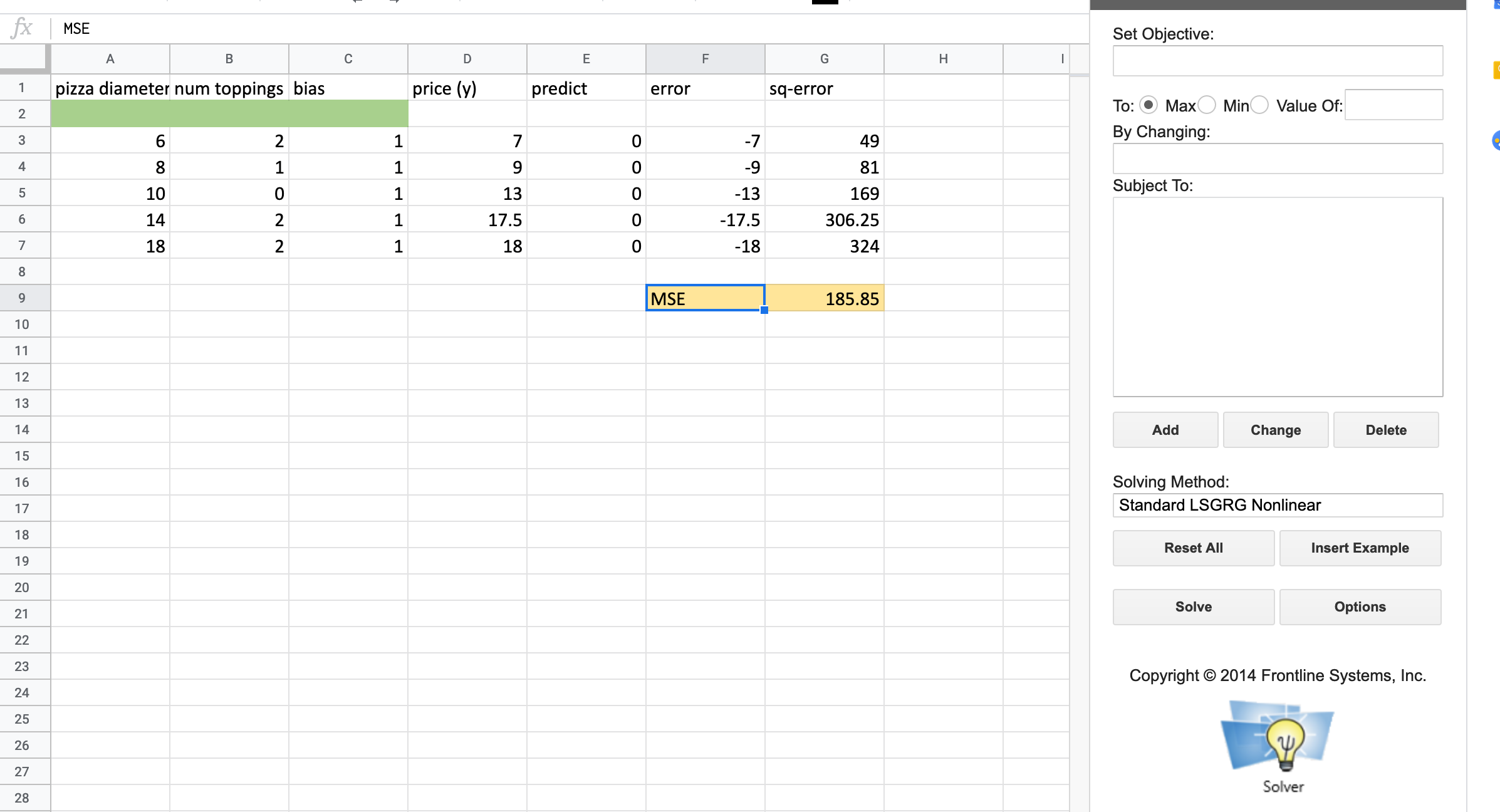
Computing the prediction for each row could be quite error-prone as there are a
lot of cells to get right. The prediction for E3 could be calculated by the
formula A$2*A3+B$2*B3+C$2*C3. You can see that this would get pretty
tiresome if you had 20 features. It is better to use SUMPRODUCT function
which does the same thing SUMPRODUCT(A$2:C$2,A3:C3). You will notice that we
fill the bias column with 1 as a placeholder for our coefficient to multiply.
You now have everything you need to set up and run Solver to create our new and improved model.
Hopefully, this little excursion back to spreadsheets has helped you develop some intuition for how regression works and what is being computed. Before we return to the bike rental problem, let’s see how we can duplicate our efforts on predicting Pizza prices in Python using Pandas and Scikit-Learn.
9.13.1. Introducing Scikit-Learn¶
Scikit-Learn is a really powerful Python package for doing all kinds of machine learning tasks. It has a consistent API so once you have learned one kind of model with Scikit-Learn you will be able to apply that to many different machine learning algorithms.
We will first create an empty model, then we will fit the model to our data. Some people also refer to this as training the model. It is essentially what we did when we pressed the Solve button on Solver. Finally, we can use the model to predict values using the model.
Create a new notebook and let’s give this a try.
First, import pandas, sklearn, and altair.
The fit method takes two parameters:
The features that we use to build the model
The known quantity that we are trying to fit the model against
Now, using the diameter and toppings make predictions about what the price will be.
If you look at those predictions, you will see they are identical to the predictions we got from the spreadsheet!
7.259036145
9.903614458
12.54819277
15.36746988
19.42168675
We can also use the mean_squared_error function supplied by sklearn to check
the mean squared error of our predictions. This function takes two parameters
the “true” values, in our case, the known price, and the predicted values.
We can also add the predictions to our dataframe so that we can graph the actual values and predicted values together.
9.13.2. Practice¶
Build another model using only the diameter and plot the predictions from that model along with the actual values and the predicted values from using both. Hint: sklearn expects to have the data it uses to build the model in a certain format. By default a single series gets converted into an array that looks like this:
But sklearn wants it to look as below. The error message you likely got tells you how to reshape the data. You can use
pdf.diameter.values.reshape(-1,1) to get the diameter into the correct
shape.
Lesson Feedback
-
During this lesson I was primarily in my...
- 1. Comfort Zone
- 2. Learning Zone
- 3. Panic Zone
-
Completing this lesson took...
- 1. Very little time
- 2. A reasonable amount of time
- 3. More time than is reasonable
-
Based on my own interests and needs, the things taught in this lesson...
- 1. Don't seem worth learning
- 2. May be worth learning
- 3. Are definitely worth learning
-
For me to master the things taught in this lesson feels...
- 1. Definitely within reach
- 2. Within reach if I try my hardest
- 3. Out of reach no matter how hard I try