Foundations of Python Programming: Functions First

The functions we’ve used as examples thus far have not been all that useful: we enclosed print() functions within our own function, as a way to illustrate parameters, when we could have just used the print() functions on their own. And, the functions we’ve defined so far don’t do much to be useful to help solve a decomposed larger problem. One of the reasons that our illustrative functions don’t appear to be useful is because few of them have returned a value. In this section we will discuss how to create more useful functions that produce useful data for our problem solving.

Functions that don’t return a value are sometimes called procedures, non-fruitful or void functions. Notice how in the function header example below the function definition indicates the function returns -> None, that there is no data being processed, and that there is no return statement. None is a special Python value used to indicate no value at all.

More usefully, a function can also be used to produce a value from from one or more parameters.

You probably can appreciate how a built-in Python function like = abs() will find, and then return, the absolute value of a provided number. Or how = input() returns anything a user types on the keyboard as a string.

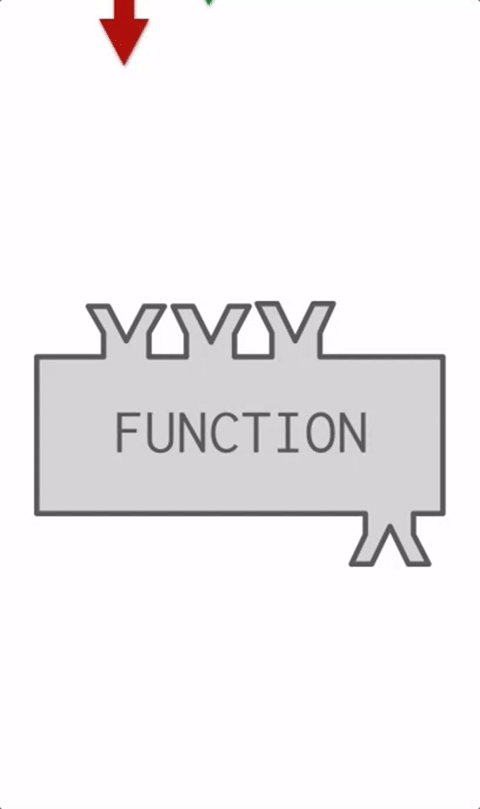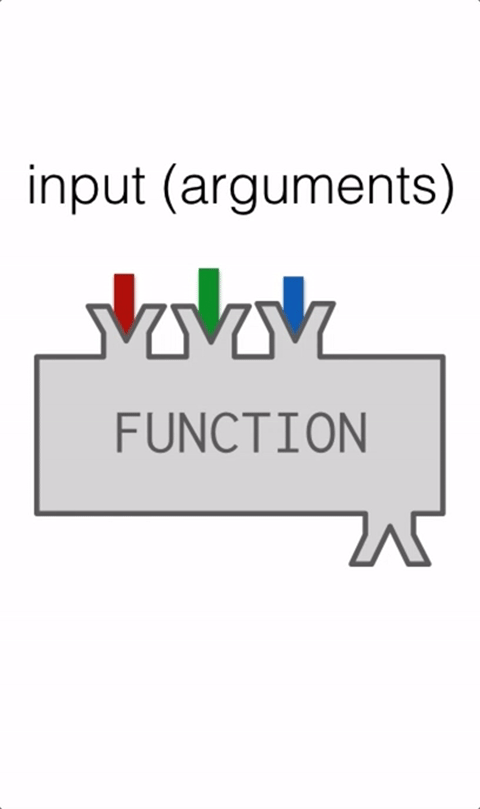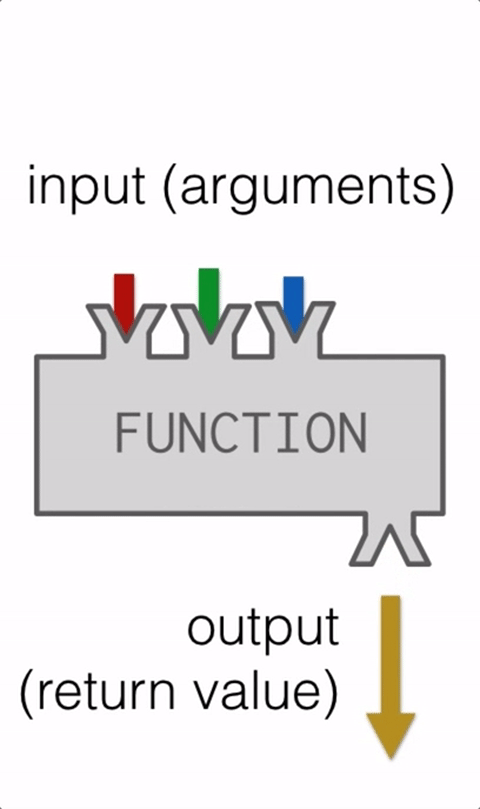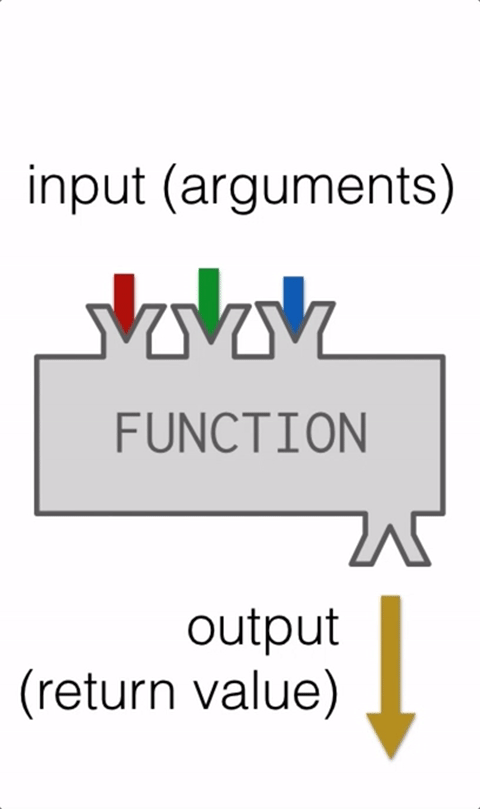
These kinds of functions, ones that return values are sometimes called fruitful functions because they produce a result.

How do we write our own fruitful function? Let’s start by creating a very simple mathematical function that we will call square. The square function will take one number as a parameter and return the result of squaring that number. Here is the black-box diagram with the Python code following.

The return statement is followed by an expression which is evaluated. Its result is returned to the caller (the line of code that invoked the function) as the “fruit” of calling this function. Because the return statement can contain any Python expression we could have avoided creating the temporary variable result and simply used return an_integer * an_integer. Try modifying the square function above to see that this works just the same. On the other hand, using temporary variables like result in the function above makes debugging easier, especially when a function is a many step process. These temporary variables are referred to as local variables. In general, programmers should not try to place a multiple step process into the return statement.

Notice something important here: the name of the variable we pass as an argument does not have to have anything to do with the name of the formal parameter — an_integer. You can see this very clearly in the Codelens: it doesn’t matter what names the caller uses — the_integer or another_integer). When square is executed, inside that function, its parameter, a local variable — an_integer, is given the value that is passed, the local temporary variable — result is determined, and finally, is the return value that the function produces.

Return the previous CodeLens example and step through the code once again. This time make note of the Frames being displayed, the appearance (and disappearance of) those variables in those frames, and the values of the variables.

When we suggested earlier that functions could be generalized, this illustrates what we meant. A fruitful function should be coded to deal with any value of parameter(s), process things, and then to provide a value based on its parameter(s). Thus, our square function can work """With any integer...""".

It should also be apparent that using self-documenting variables names, like the_integer and another_integer, make clearer what is being passed to the function and what variables are local to the function (an_integer and result). And, using these kinds of self-documenting variable names makes the code easier to design, develop and debug.

There is one more aspect of fruitful functions. By default, all Python functions return the special value None to indicate there is no value at all. This is not the same as 0, False, nor an empty string "".

Notice in the following how the square function does not contain a return statement. As you step through this example, pay very close attention to the Return Value in the square function’s frame. Then look at what is printed when the function is over.

A problem with this function is that even though it prints the resulting squared value (line 3), that value will not be available to be subsequently displayable, accessed nor used after the function has been executed. Instead, the value None will be returned to the caller’s scope. Since line 6 assigns the function’s return value to square_result, that variable will have None as its value and that is what will be printed in line 7.

Much more usefully one would code a fruitful function that return a value and assigns that value to a variables for later processing or display.

Next, a return statement, once executed, immediately terminates execution of a function, even if it is not the last statement in the function. In the following code, when line 3 executes, the value 5 is returned and assigned to the variable x, then printed. Lines 4 and 5 never execute. Run the following code and try making some modifications of it to make sure you understand why “there” and 10 never print out.

The fact that a return statement immediately ends execution of the code block inside a function is important to understand for writing complex programs. The following example algorithm uses a programming structure, conditionals, that we will cover later, but for now we will use the idea here to hint at what is possible.

Consider a circumstance where a student’s grade has to be greater than or equal to 60% to use it as a prerequisite. A function to check this could be written as follows:

def prerequisite_checker( grade: float ) -> bool:
    """Checks if student meets prerequisite grade requirements"""
    if grade < 60:
        return False
    else:
        return True

Do consider the challenges with using multiple return statements: the programmer (and thus the function’s code) has to repeat the return statement for every circumstance - and cannot overlook even one outcome. In fact, the structured programming tradition considers the use of multiple return statements to be bad practice. Instead, it suggests programmers get into the habit of always having a single return statement as very last line of their function’s body, to avoid ’forgetting’ to include all the returns. This practice, making the last line of every function a return statement, also makes tracing and debugging the complex function code easier.

So far, we have just seen return values being assigned to variables. For example, we had the line square_result = square(the_integer). As with all assignment statements, the right-hand side of that instruction is executed first. It invokes the square function, passing in a parameter value 10 (the current value of the_integer). The function returns a value 100, which completes the evaluation of the right-hand side of the assignment. The value 100 is then assigned to the variable square_result. In this case, the function invocation was the entire expression that was evaluated.

Function invocations, however, can also be used as part of more complicated expressions. For example, square_result = 2 * square(the_integer + 1). In this case, the value 11 is evaluated, passed to the function, and is returned to the right-hand side of the instructions. Then, the returned value (121) is multiplied by 2 to produce the value 242.

To reiterate, when executing the line of code square_result = 2 * square(the_integer + 1), the Python interpreter does these steps: