5.10. Tower of Hanoi¶
The Tower of Hanoi puzzle was invented by the French mathematician Edouard Lucas in 1883. He was inspired by a legend that tells of a Hindu temple where the puzzle was presented to young priests. At the beginning of time, the priests were given three poles and a stack of 64 gold disks, each disk a little smaller than the one beneath it. Their assignment was to transfer all 64 disks from one of the three poles to another, with two important constraints. They could only move one disk at a time, and they could never place a larger disk on top of a smaller one. The priests worked very efficiently, day and night, moving one disk every second. When they finished their work, the legend said, the temple would crumble into dust and the world would vanish.
Although the legend is interesting, you need not worry about the world ending any time soon. The number of moves required to correctly move a tower of 64 disks is \(2^{64}-1 = 18,446,744,073,709,551,615\). At a rate of one move per second, that is \(584,942,417,355\) years! Clearly there is more to this puzzle than meets the eye.
Figure 1 shows an example of a configuration of disks in the middle of a move from the first peg to the third. Notice that, as the rules specify, the disks on each peg are stacked so that smaller disks are always on top of the larger disks. If you have not tried to solve this puzzle before, you should try it now. You do not need fancy disks and poles–a pile of books or pieces of paper will work.
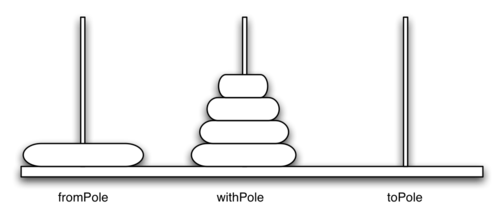
Figure 1: An Example Arrangement of Disks for the Tower of Hanoi¶
How do we go about solving this problem recursively? How would you go about solving this problem at all? What is our base case? Let’s think about this problem from the bottom up. Suppose you have a tower of five disks, originally on peg one. If you already knew how to move a tower of four disks to peg two, you could then easily move the bottom disk to peg three, and then move the tower of four from peg two to peg three. But what if you do not know how to move a tower of height four? Suppose that you knew how to move a tower of height three to peg three; then it would be easy to move the fourth disk to peg two and move the three from peg three on top of it. But what if you do not know how to move a tower of three? How about moving a tower of two disks to peg two and then moving the third disk to peg three, and then moving the tower of height two on top of it? But what if you still do not know how to do this? Surely you would agree that moving a single disk to peg three is easy enough, trivial you might even say. This sounds like a base case in the making.
Here is a high-level outline of how to move a tower from the starting pole, to the goal pole, using an intermediate pole:
Move a tower of height-1 to an intermediate pole, using the final pole.
Move the remaining disk to the final pole.
Move the tower of height-1 from the intermediate pole to the final pole using the original pole.
As long as we always obey the rule that the larger disks remain on the bottom of the stack, we can use the three steps above recursively, treating any larger disks as though they were not even there. The only thing missing from the outline above is the identification of a base case. The simplest Tower of Hanoi problem is a tower of one disk. In this case, we need move only a single disk to its final destination. A tower of one disk will be our base case. In addition, the steps outlined above move us toward the base case by reducing the height of the tower in steps 1 and 3. Listing 1 shows the Python code to solve the Tower of Hanoi puzzle.
Listing 1
1int moveTower(int height, char fromPole, char toPole, char withPole){
2 if (height >= 1){
3 moveTower(height-1, fromPole, withPole, toPole);
4 moveDisk(fromPole, toPole);
5 moveTower(height-1, withPole, toPole, fromPole);
6 }
7}
Notice that the code in Listing 1 is almost identical to the
English description. The key to the simplicity of the algorithm is that
we make two different recursive calls, one on line 3 and a
second on line 5. On line 3 we move all but the bottom
disk on the initial tower to an intermediate pole. The next line simply
moves the bottom disk to its final resting place. Then on line
5 we move the tower from the intermediate pole to the top of
the largest disk. The base case is detected when the tower height is 0;
in this case there is nothing to do, so the moveTower function
simply returns. The important thing to remember about handling the base
case this way is that simply returning from moveTower is what
finally allows the moveDisk function to be called.
The function moveDisk, shown in Listing 2, is very
simple. All it does is print out that it is moving a disk from one pole
to another. If you type in and run the moveTower program you can see
that it gives you a very efficient solution to the puzzle.
Listing 2
int moveDisk(char fp, char tp){
cout << "moving disk from " << fp << " to " << tp << endl;
}
The program in ActiveCode 1 provides the entire solution for three disks.
Now that you have seen the code for both moveTower and moveDisk,
you may be wondering why we do not have a data structure that explicitly
keeps track of what disks are on what poles. Here is a hint: if you were
going to explicitly keep track of the disks, you would probably use
three Stack objects, one for each pole. The answer is that C++
provides the stacks that we need implicitly through the call stack.