8.25. Discussion Questions¶
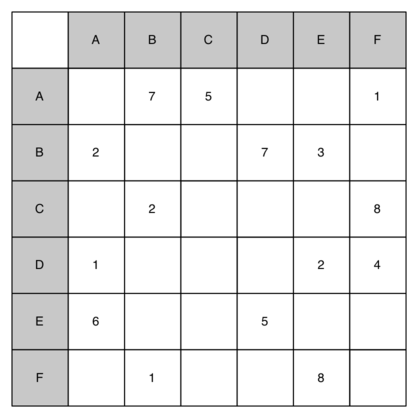
Draw the graph corresponding to the following adjacency matrix.
Draw the graph corresponding to the following list of edges.
from
to
cost
1
2
10
1
3
15
1
6
5
2
3
7
3
4
7
3
6
10
4
5
7
6
4
5
5
6
13
Ignoring the weights, perform a breadth first search on the graph from the previous question.
- O(n)
- O(n) would suggest that there is no nesting. There are several nested for loops.
- O(n2)
- Correct. The two consecutively nested for loops would dictate that this is in the realm of O(n2).
- O(1)
- O(1) would suggest that the function is constant. Since there are multiple for loops intertwined, it is not in constant time.
- O(n3)
- O(n3) would suggest that there are three consecutively nested for loops. There are only two.
Q-2: 4. What is the Big-O running time of the buildGraph function?
Q-3: 5. Derive the Big-O running time for the topological sort algorithm.
Q-4: 6. Derive the Big-O running time for the strongly connected components algorithm.
Show each step in applying Dijkstra’s algorithm to the graph shown above.
Using Prim’s algorithm, find the minimum weight spanning tree for the graph shown above.
Draw a dependency graph illustrating the steps needed to send an email. Perform a topological sort on your graph.
Derive an expression for the base of the exponent used in expressing the running time of the knights tour.
- Q-6: 11. Explain why the general DFS algorithm is not suitable for solving
the knights tour problem.
- Q-7: 12. What is the Big-O running time for Prim’s minimum
spanning tree algorithm?
- O(1)
- O(1) would mean that the algorithm runs in constant time. This isn't true because there are several comparisons happening in the algorithm.
- O(n3)
- O(n3) suggests that there are three consecutively nested loops. If you look at the example algorithm, it is obvious that there are not three nested loops.
- O(n)
- O(n) is linear time. The time it takes for this program to run doesn't grow linearly.
- O(n2)
- Correct. Since you are not only comparing the weight of a branch but also if the branch has already been connected to, this would make the Big-O of the algorithm O(n2)