19.3. Objects Revisited¶
In Python, every value is actually an object. Whether it be a turtle, a list, or even an integer, they are all objects. Programs manipulate those objects either by performing computation with them or by asking them to perform methods. To be more specific, we say that an object has a state (also called attributes or properties) and a collection of methods (also called behavior) that it can perform. The state of an object represents those things that the object knows about itself. For example, as we have seen with turtle objects, each turtle has a state consisting of the turtle’s position, its color, its heading and so on. Each turtle also has the ability to go forward, backward, or turn right or left. Individual turtles are different in that even though they are all turtles, they differ in the specific values of the individual state attributes (maybe they are in a different location or have a different heading).
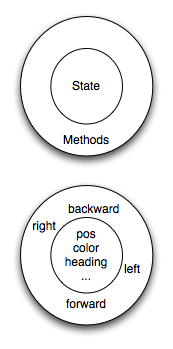
- pos (x and y position)
- Turtle objects know their position.
- pen color
- Turtle objects know their pen color.
- forward
- This is a behavior (something the object can do) not an attribute (data about itself).
- left
- This is a behavior (something the object can do) not an attribute (data about itself).
Q-1: Which of the following is/are attributes (state) for objects of the Turtle class?