7.5. Functions Calling Functions - 1

Much in the same way we can use a procedure drawSquare to help write code for a more complex procedure like drawGrid, we can use existing functions to help write new functions.

When solving complex problems, we can use this trick to avoid repeating code and to make abstractions that make a program easier to read and write.

Say we are starting with the coordinates of the three points of a triangle and we want to calculate the area of the shape. There is a formula called Heron’s formula that we can use to find the area of a triangle: \(\sqrt{s (s - a) (s - b) (s - c)}\) where s is the semi-perimeter (half the perimeter) and a, b, c are the lengths of the three sides.

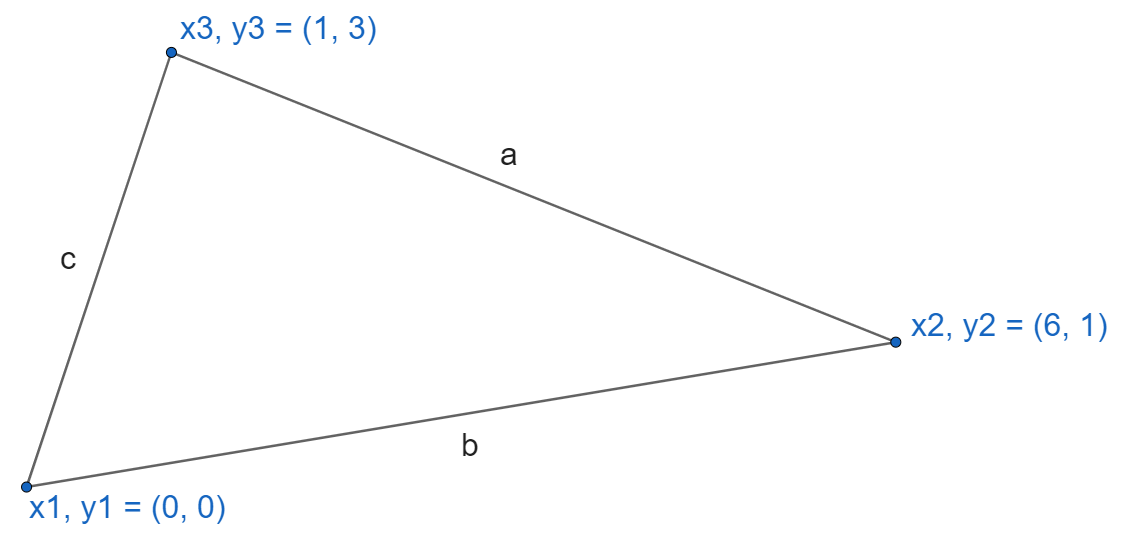
A triangle with sides labled a, b, and c.

That sounds too complex to do in a short amount of code. So let’s break down the problem. Before we can use that formula, we need to know the lengths of the three sides. We can use the distance formula to calculate them: \(\sqrt{(x2-x1)^2 + (y2-y1)^2}\). Let’s make a function to do that job.

When designing functions, we need to define them in terms of their inputs (parameters) and their outputs (what they return). Our distance functions will take in two x,y pairs and it will return the distance between them:

def distance(x1, y1, x2, y2):
    Do work to calculate distance.
    return distance

Let’s start by writing that and testing it. We will make a function distance that has parameters for the x and y of two different points.

This program has the function, and tests for sideA and sideB. Try running it. Then add a test for sideC that connects point1 and point3. Call the distance formula with the correct arguments and store the result into sideC (Hint, the correct answer is ~3.16, but you must actually use the distance function to calculate it.)

def distance(x1, y1, x2, y2): xDifference = x2 - x1 yDifference = y2 - y1 distance = math.sqrt( xDifference ** 2 + yDifference ** 2 ) return distance # Main program import math point1x = 0 point1y = 0 point2x = 6 point2y = 2 point3x = 1 point3y = 3 sideA = distance(point1x, point1y, point2x, point2y) print(sideA) sideB = distance(point2x, point2y, point3x, point3y) print(sideB) # Your test here ==== from unittest.gui import TestCaseGui class myTests(TestCaseGui): def testOne(self): self.assertAlmostEqual(sideC, 3.16227766, 3, "Testing that you printed the right length for sideC.") self.assertNotRegex(self.getEditorText(), "3\.16", "Testing that you did not hard code the answer.") myTests().main()

You have attempted of activities on this page