8.13. Sorting Efficiency¶
To figure out how efficient the Selection Sort algorithm is, we will analyze the worst case. For units of work, we will consider comparisons and swaps - the two key operations in a sort. This video works through how much work there is for a Selection Sort on a list of 4 items:
Animation used by permission of Virginia Tech
If we did the same work for a selection sort on a list of 100 things (\(n = 100\)), it would look like:
Step |
Comparisons |
Swaps |
|---|---|---|
1 |
99 |
1 |
2 |
98 |
1 |
3 |
97 |
1 |
… |
… |
… |
97 |
3 |
1 |
98 |
2 |
1 |
99 |
1 |
1 |
The total swaps would be 99 steps times 1 swap each = 99. Expressed in terms of \(n\) we could say it is \(n - 1\) swaps.
The total comparisons would be 99 + 98 + 97 + … + 3 + 2 + 1 or \((n - 1) + (n - 2) + (n - 3) + ... + 3 + 2 + 1\). So what does that equal? There is a trick to find out - pair up the first item and the last, then the second item and next to last and so on. Each pair of items sums to \(n\):
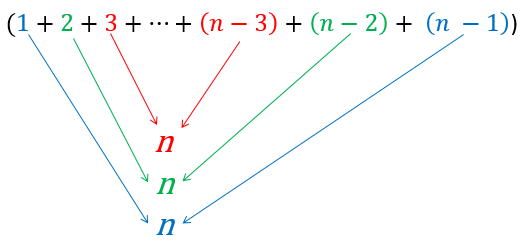
Since there were \(n - 1\) numbers to start with, there will be \(\frac{n - 1}{2}\) pairs, each of which adds to \(n\). Multiplying the number of pairs by the sum of each pair gives us the total: \(\frac{n - 1}{2} \cdot n = \frac{n^2 - n}{2} = \frac{n^2}{2} - \frac{n}{2}\).
Overall, our work will be given by:
\(\text{Total work} = \text{Comparisons} + \text{Swaps}\)
Or:
\(\textrm{Total work} = (\frac{n^2}{2} - \frac{n}{2}) + (n-1) = \frac{n^2}{2} + \frac{n}{2} - 1\)
Since for Big-O purposes, all we care about is the class of the dominant term, in this case \(\frac{n^2}{2}\), we will say that Selection Sort is \(O(n^2)\) (Quadratic). A similar process can be used to show that so is Insertion Sort.
Important
Selection and Insertion Sort are Quadratic - \(O(n^2)\).
