4.7. Group Work - Remainder Operator (%)¶
It is best to use a POGIL approach with the following. In POGIL students work in groups on activities and each member has an assigned role. For more information see https://cspogil.org/Home. This page is based on a POGIL activity from Helen Hu at that site.
Run the following code to see what it prints.
Look at the expressions in the code above and the output. Then answer the following questions.
4-7-2: Review the code above. What is the first number (n) above such that n % 4 returns zero?
4-7-3: Review the code above. What is the next number (n) (greater than 16) such that n % 4 returns zero?
4.7.1. Going Beyond Remainder 4¶
4-7-4: What is the first number from to 1 to 10 that is evenly divisible by five (n % 5 returns 0)?
4-7-5: What is the last number from to 1 to 10 that is evenly divisible by five (n % 5 returns 0)?
4.7.2. Look Deeper¶
4-7-6: Look at the code above for the numbers such that n % 4 returns 1. How do these numbers differ from the ones that return zero?
4.7.3. More Practice¶
4-7-7: What is the number returned from 18 % 4?
4-7-8: What is the number returned from 19 % 4?
4-7-9: What is the number returned from 19 % 5?
4-7-10: What is the number returned from 19 % 6?
4.7.4. Long Division with a Remainder¶
Consider how you did long division in elementary school where you determined what number goes evenly into another number and the remainder.
4-7-11: What number is the remainder when you divide 79 by 5?
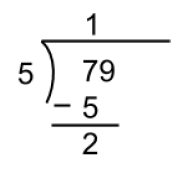
4.7.5. Dividing Evenly¶
Imagine if you were given candies to evenly divide amoung members of a group of four people. Follow kindergarten rules where every group member gets the same number of candies and the extras go back to the teacher.
4-7-12: How many candies go back to the teacher when you are given 11 candies?
4-7-13: How many candies go back to the teacher when you are given 2 candies?
4.7.6. Describe the Remainder (%) Operator¶
4-7-14: Describe what % does in your own words. Use complete sentences.