Time estimate: 45 min.

10.1.1. What is Recursion? (Day 1)¶

Recursion is when a method calls itself. See the example method below.

public static void neverEnd()
{
  System.out.println("This is the method that never ends!");
  neverEnd();
}

This method will print out “This is the method that never ends!” and then call itself, which will print out the message again, and then call itself, and so on. This is called infinite recursion, which is a recursion that never ends. Of course, this particular method is not very useful. (Actually, in practice it will end, crashing with a StackOverFlowError because there is a limit on how many times you can recurse.)

Check your Understanding

10-1-1: Which line in the method neverEnd (shown above) contains the recursive call (the call to the same method)?

10-1-2: Is the following method recursive?

public static int mystery()
{
   int total = 0;
   for (int i=10; i>0; i--)
   {
      total = total + i;
   }
   return total;
}

Yes
Where is the call to the same method?
No
There is no call to the same method, so this can not be a recursive method. It uses iteration instead.

10-1-3: Is the following method recursive?

public static int mystery2(int x)
{
   if (x == 1) return 1;
   else return x + mystery2(x-1);
}

Yes
Yes, any method that contains at least one call to the same method is recursive.
No
Look again. Check if the method contains a call to itself.

10.1.2. Why use Recursion?¶

Recursion is most useful for solving problems where the structure of the problem allows it to be broken into smaller, but similar problems, whose solutions can be combined into the solution to the original problem.

For example, suppose you wanted to find out how much space a folder on your computer uses? Well, if you knew how much space each of the files and sub-folders in that folder used, you could add them up and get the answer. Getting the size of a regular file is usually easy, but figuring out how much space each sub-folder takes up is the same problem we stared with, just with a different folder.

But that’s actually great news because we can use the same procedure to solve this smaller problem: find the size of all the files and sub-folders in it and add them up. Eventually, as we try to get the size more deeply nested folders, eventually we’ll get to folders that only contain plain files whose sizes we can add up and return and eventually we work our way back up to give the answer to our question about the original top-most folder.

Recursion can also be used to create fractals. A simple example is Sierpinski’s triangle in which you subdivide a triangle into 4 new triangles as shown below. You can then do the some procedure with each new triangle except the center one.

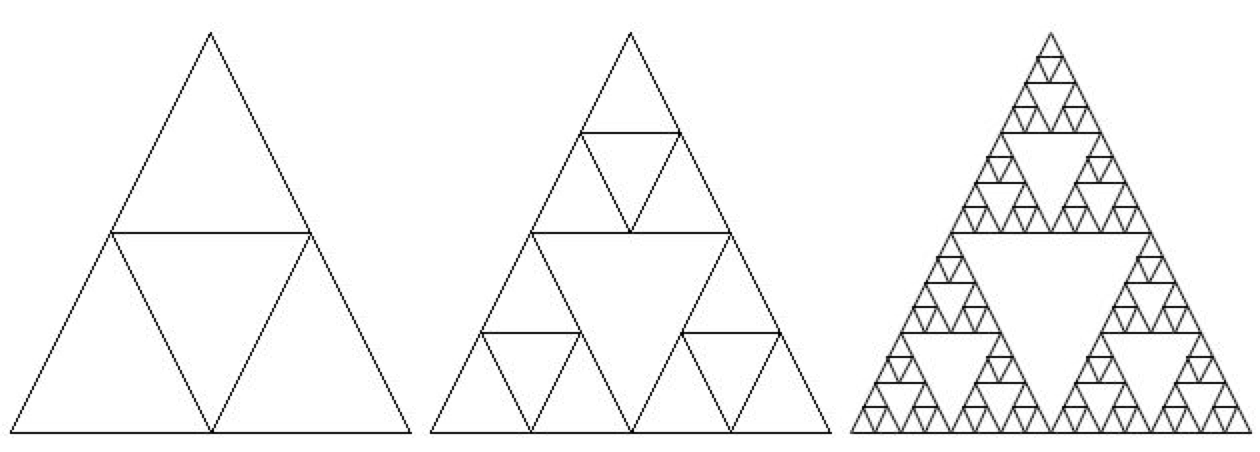
../_images/triangleSub.png — Figure 1: A sequence of Sierpinski’s triangles¶

Recursion can also be used to traverse Strings, arrays, and ArrayLists just like a loop. In fact, any loop—also known as iterative code—can be written using recursion. However in most languages, including Java, there are limitations on how deeply code can recurse which rules out using recursion for infinite or even very long loops so we don’t usually use recursion when a simple loop will do.

On the other hand, recursion is more powerful than simple loops, especially when dealing with branching structures like the file folder example. Computer scientists call such structures “trees” and they incredibly common in computer programs.

Recursive procedures that operate on trees often cannot be easily translated into simple loops, at least not without using some extra data structures to keep track where you are in the tree. Thus one way to think about recursion is as “loops for trees”. If you need to loop over a simple linear structure like a String or an array, by all mean use a for loop. And if you want to navigate a 2D array a pair of nested for loops is the way to go. But if you need to traverse a tree structure, recursion should be your go to.

10.1.3. Factorial Method¶

The following video is also on YouTube at https://youtu.be/V2S_8E_ubBY. It introduces the concept of recursion and tracing recursion with the factorial method.

See the method factorial below that calculates the factorial of a number. The factorial of a number is defined as 1 for 0 and n * factorial (n-1) for any other number.

public static int factorial(int n)
{
    if (n == 0)
        return 1;
    else
        return n * factorial(n-1);
}

You can also play with an interactive demonstration of the recursive factorial computation at https://gigamonkeys.com/misc/factorial/#java.

Check your understanding

10-1-5: Which line in the method factorial contains the recursive call (the call to the same method)?

Coding Exercise

Run the code below to test the factorial method. What’s the factorial of 6? Add another test to print out the factorial of 6. What’s the factorial of 1? Add another test to print out the factorial of 1.

public class FactorialTest
{

public static int factorial(int n)
    {
        if (n == 0) return 1;
        else return n * factorial(n - 1);
    }

public static void main(String[] args)
    {
        System.out.println("factorial of 3 is: " + factorial(3));
        System.out.println("factorial of 4 is: " + factorial(4));
        System.out.println("factorial of 5 is: " + factorial(5));
    }
}

====
import static org.junit.Assert.*;

import org.junit.*;

import java.io.*;

public class RunestoneTests extends CodeTestHelper
{
    @Test
    public void testMain() throws IOException
    {
        String output = getMethodOutput("main");
        String expect =
                "factorial of 3 is: 6\n"
                    + "factorial of 4 is: 24\n"
                    + "factorial of 5 is: 120\n"
                    + "factorial of 6 is: 720\n"
                    + "factorial of 1 is: 1\n";
        boolean passed = getResults(expect, output, "Expected output from main");
        assertTrue(passed);
    }
}

10.1.4. Base Case¶

Every non-infinite recursive method must have at least one base case where the method can return an answer without another recursive call. In other words, the base case is the smallest possible problem (or problems) that the method knows how to solve, the ones it can answer directly without any more recursion.

The base case is often handled by an if statement that checks for the base case and returns directly when the condition for the base case is met.

In the factorial method, the base case is when the argument is 0 as that is the smallest number that the factorial method can handle since factorial isn’t defined for negative numbers.

When we recurse through folders on our computer there are two base cases, a simple file, whose size we can find out directly, and an empty folder whose size is 0 (or maybe some other fixed amount, depending on the operating system). In those two cases a method to compute the space used by a file or folder could return immediately; in all others it would have to recurse to get the sizes of the files and sub-folders it contains and then add them up.

The goal of every recursive call in a recursive method is to shrink the problem in some way that gets closer to the base case. You can see that in factorial where the recursive call is passing n - 1, one closer to 0. If you write a recursive method (not required for the AP exam), you should make sure that every time you recurse you are shrinking the problem so it is closer to the base case—that’s the equivalent in recursion to incrementing your loop variable in a for loop.

Check your understanding

10-1-7: Click on the line or lines that contain the test for the base caseWhen a base case test is true a value is returned and the recursion stops.

public static int factorial(int n)
{
    if (n == 0)
        return 1;
    else
        return n * factorial(n-1);
}

10-1-8: What is the value of n when this method stops calling itself (when it reaches the base case)?

public static int product(int n)
{
   if(n == 1)
      return 1;
   else
      return n * product(n - 2);
}

0
Look again. What is the value of n when this method returns a value, without doing a recursive call?
1
This method stops calling itself when n equals 1 (line 3).
2
Look for a return with a number after it. When is this code executed?

10-1-9: What is/are the values of the variable bunnies when this method stops calling itself (when it reaches the base case)?

public static int bunnyEars(int bunnies)
{
   if (bunnies == 0) return 0;
   else if (bunnies == 1) return 2;
   else return 2 + bunnyEars(bunnies - 1);
}

0
This method also stops for another value of bunnies.
1
This method also stops for another value of bunnies.
Both 0 and 1
This method stops calling itself when bunnies is either 0 or 1.

10-1-10: Is the following method recursive?

public static int bunnyEars(int bunnies)
{
   int total = 0;
   for (int i = 0; i < bunnies; i++)
   {
      total = total + 2;
   }
   return total;
}

yes
Where is the call to the same method?
no
There is no call to the same method, so it is not recursive. This uses iteration instead.

Continue to the next page for Day 2 of the Recursion lesson.

You have attempted of activities on this page