5.5. WS Graphs

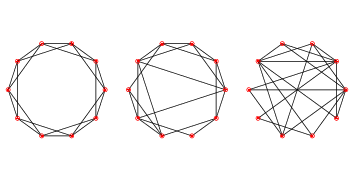
Figure 5.2: WS graphs with \(n=20\), \(k=4\), and \(p=0\) (left), \(p=0.2\) (middle), and \(p=1\) (right).

To make a Watts-Strogatz (WS) graph, we start with a ring lattice and “rewire” some of the edges. In their paper, Watts and Strogatz consider the edges in a particular order and rewire each one with probability \(p\). If an edge is rewired, they leave the first node unchanged and choose the second node at random. They don’t allow self loops or multiple edges; that is, you can’t have a edge from a node to itself, and you can’t have more than one edge between the same two nodes.

Here is an implementation of this process.

def rewire(G, p):
nodes = set(G)
for u, v in G.edges():
    if flip(p):
        choices = nodes - {u} - set(G[u])
        new_v = np.random.choice(list(choices))
        G.remove_edge(u, v)
        G.add_edge(u, new_v)

The parameter p is the probability of rewiring an edge. The for loop enumerates the edges and uses flip (defined below) to choose which ones get rewired.

def flip(p):
    return np.random.random() < p

flip uses a module from NumPy (which is imported as np in this example) named random. This module has a method also named random, which returns a number between 0 and 1.

flip returns True when the random number is less than the given probability p, it returns false when the random number is greater than or equal to p.

If we are rewiring an edge from node u to node v, we have to choose a replacement for v, called new_v.

1. To compute the possible choices, we start with nodes, which is a set, and subtract off u and its neighbors, which avoids self loops and multiple edges.

2. To choose new_v, we use the NumPy function choice, which is in the module random.

3. Then we remove the existing edge from u to v, and

4. Add a new edge from u to new_v.

As an aside, the expression G[u] returns a dictionary that contains the neighbors of u as keys. It is usually faster than using G.neighbors.

This function does not consider the edges in the order specified by Watts and Strogatz, but that doesn’t seem to affect the results.

Figure 5.2 shows WS graphs with \(n=20\), \(k=4\), and a range of values of p. When \(p=0\), the graph is a ring lattice. When \(p=1\), it is completely random. As we’ll see, the interesting things happen in between.

Q-1: As demonstrated in figure 4.2, what happens as p increases?

• The graph becomes more like a lattice.
• Look again at the picture on the right where p is at its highest.
• The graph becomes more consistent.
• Look again of what happens as p goes higher.
• No rewiring happens.
• p is the probability that something is rewired.
• The graph becomes more random.
• Correct!

You have attempted of activities on this page