4.5. Generating Graphs¶
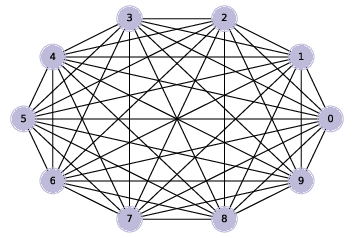
Figure 4.3: A complete graph with 10 nodes.¶
We’ll start by generating a complete graph, which is a graph where every node is connected to every other.
Here’s a generator function that takes a list of nodes and enumerates all distinct pairs. If you are not familiar with generator functions.
def all_pairs(nodes):
for i, u in enumerate(nodes):
for j, v in enumerate(nodes):
if i>j:
yield u, v
We can use all_pairs to construct a complete graph:
def make_complete_graph(n):
G = nx.Graph()
nodes = range(n)
G.add_nodes_from(nodes)
G.add_edges_from(all_pairs(nodes))
return G
make_complete_graph takes the number of nodes, n, and returns a new Graph with n nodes and edges between all pairs of nodes.
The following code makes a complete graph with 10 nodes and draws it:
complete = make_complete_graph(10)
nx.draw_circular(complete,
node_color=COLORS[2],
node_size=1000,
with_labels=True)
Figure 4.3 shows the result. Soon we will modify this code to generate ER graphs, but first we’ll develop functions to check whether a graph is connected.
You have attempted of activities on this page