8.4. Conway’s Conjecture¶
From most initial conditions, GoL quickly reaches a stable state where the number of live cells is nearly constant (possibly with some oscillation).
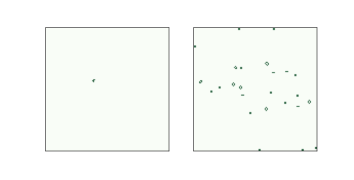
Figure 8.4: Starting and final configurations of the r-pentomino.¶

Gif of Starting and final configurations of the r-pentomino.¶
But there are some simple starting conditions that yield a surprising number of live cells, and take a long time to settle down. Because these patterns are so long-lived, they are called “Methuselahs”.
One of the simplest Methuselahs is the r-pentomino, which has only five cells, roughly in the shape of the letter “r”. Figure 8.4 shows the initial configuration of the r-pentomino and the final configuration after 1103 steps.
This configuration is “final” in the sense that all remaining patterns are either stable, oscillators, or gliders that will never collide with another pattern. In total, the r-pentomino yields 6 gliders, 8 blocks, 4 blinkers, 4 beehives, 1 boat, 1 ship, and 1 loaf.
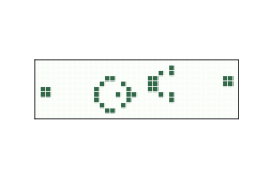
Figure 8.5: Gosper’s glider gun, which produces a stream of gliders.¶

Gif of Gosper’s glider gun, which produces a stream of gliders.¶
The existence of long-lived patterns prompted Conway to wonder if there are initial patterns that never stabilize. He conjectured that there were not, but he described two kinds of pattern that would prove him wrong, a “gun” and a “puffer train”. A gun is a stable pattern that periodically produces a spaceship — as the stream of spaceships moves out from the source, the number of live cells grows indefinitely. A puffer train is a translating pattern that leaves live cells in its wake.
It turns out that both of these patterns exist. A team led by Bill Gosper discovered the first, a glider gun now called Gosper’s Gun, which is shown in Figure 8.5. Gosper also discovered the first puffer train.
There are many patterns of both types, but they are not easy to design or find. That is not a coincidence. Conway chose the rules of GoL so that his conjecture would not be obviously true or false. Of all possible rules for a 2-D CA, most yield simple behavior: most initial conditions stabilize quickly or grow unboundedly. By avoiding uninteresting CAs, Conway was also avoiding Wolfram’s Class 1 and Class 2 behavior, and probably Class 3 as well.
If we believe Wolfram’s Principle of Computational Equivalence, we expect GoL to be in Class 4, and it is. The Game of Life was proved Turing complete in 1982 (and again, independently, in 1983). Since then, several people have constructed GoL patterns that implement a Turing machine or another machine known to be Turing complete.
- It is a Methuselahs
- Correct! It has a simple starting condition and is long-lived.
- It is a beehive
- Sorry a beehive is a stable pattern with each cell having two to three neighbors , so they all survive, and none of the dead cells adjacent to the beehive has 3 neighbors, so no new cells are born.
- It only has five cells
- Correct!
- It was one of the two patterns that Conway said would never stabilize and prove him wrong
- Sorry the two patterns that Conway said could prove him wrong were actually a “gun” and a “puffer train”.
- None of the above are true
- Sorry but two of the answers given above are correct.
Q-2: Which of the following is true about r-pentomino? Select all that apply.
- True
- Correct, Gosper's gun is the same gun that Conway said would prove him wrong.
- False
- Incorrect
Q-3: There was a prediction of Gosper’s gun, a stable pattern that periodically produces a spaceship. As the stream of spaceships move out from the source, the number of live cells grows indefinitely.