13.8. Differential Survival¶
Let’s add one more ingredient, differential survival. Here’s a class that extends Simulation and overrides choose_dead:
class SimWithDiffSurvival(Simulation):
def choose_dead(self, fits):
n = len(self.agents)
is_dead = np.random.random(n) > fits
index_dead = np.nonzero(is_dead)[0]
return index_dead
Now the probability of survival depends on fitness; in fact, in this version, the probability that an agent survives each time step is its fitness.
Since agents with low fitness are more likely to die, agents with high fitness are more likely to survive long enough to reproduce. Over time we expect the number of low-fitness agents to decrease, and the number of high-fitness agents to increase.
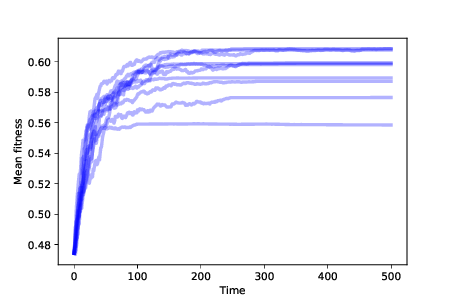
Figure 13.2: Mean fitness over time for 10 simulations with differential survival.¶
Figure 13.2 shows mean fitness over time for 10 simulations with differential survival. Mean fitness increases quickly at first, but then levels off.
You can probably figure out why it levels off: if there is only one agent at a particular location and it dies, it leaves that location unoccupied. Without mutation, there is no way for it to be occupied again.
With N=8, this simulation starts with 256 agents occupying all possible locations. Over time, the number of occupied locations decreases; if the simulation runs long enough, eventually all agents will occupy the same location.
So this simulation starts to explain adaptation: increasing fitness means that the species is getting better at surviving in its environment. But the number of occupied locations decreases over time, so this model does not explain increasing diversity at all.
In the notebook for this chapter, you will see the effect of differential reproduction. As you might expect, differential reproduction also increases mean fitness. But without mutation, we still don’t see increasing diversity.
- Adaptation.
- Correct! Increasing fitness means that the species is getting better at surviving in its environment.
- The increasing diversity.
- Incorrect, the number of occupied locations decreases over time, so this model does not explain increasing diversity at all.
- The decrease in mean fitness.
- Incorrect, the decrease in mean fitness is not explained by simulation.
- Increase of locations occupied over time.
- Incorrect, the number of occupied locations decrease.
Q-1: What does the simulation above explain?