Motivating Questions
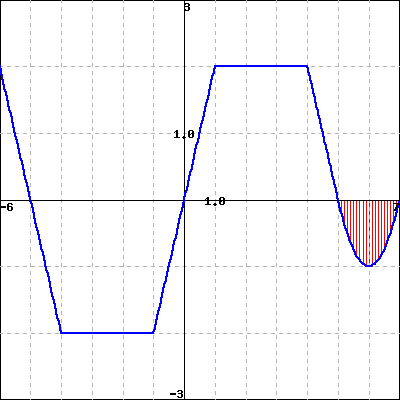
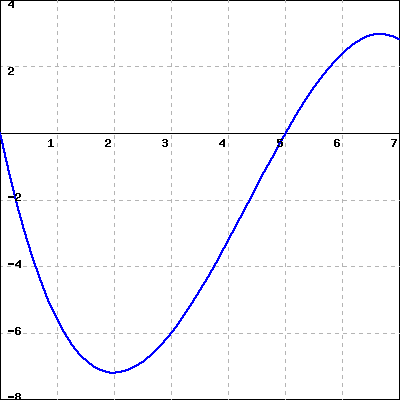
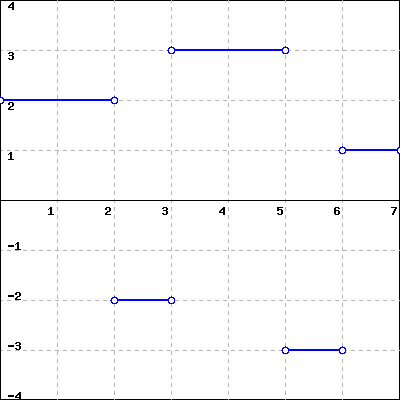
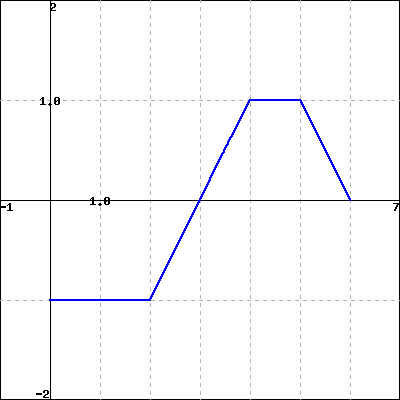
- Given the graph of a function’s derivative, how can we construct a completely accurate graph of the original function?
- How many antiderivatives does a given function have? What do those antiderivatives all have in common?
- Given a function \(f\text{,}\) how does the rule \(A(x) = \int_0^x f(t) \, dt\) define a new function \(A\text{?}\)